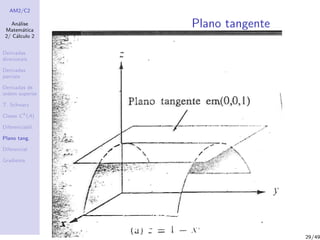
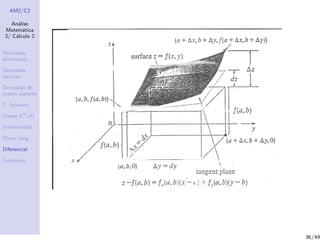
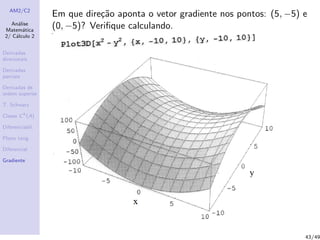
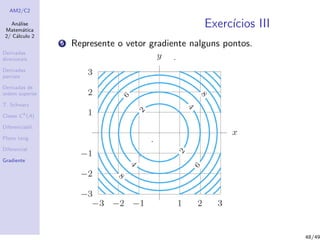
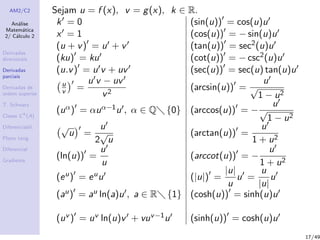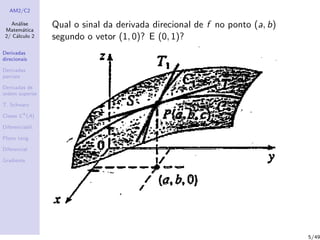
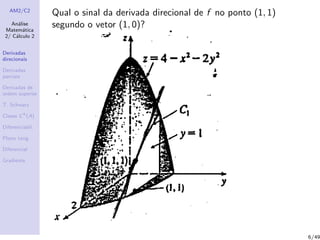
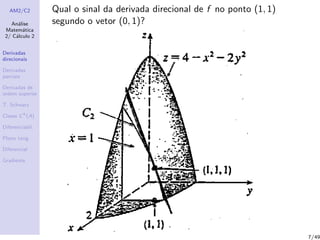
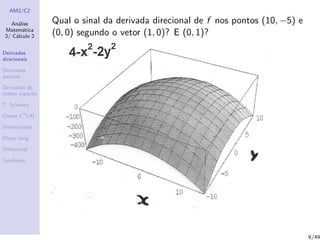
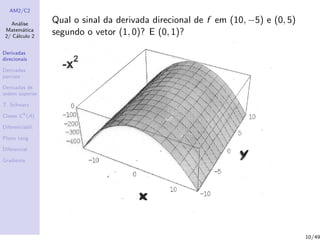
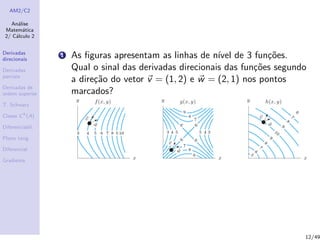
O documento apresenta conceitos fundamentais de cálculo diferencial, incluindo: 1) Derivadas direcionais, definidas como a taxa de variação de uma função em uma direção dada por um vetor no ponto; 2) Derivadas parciais, que são derivadas direcionais segundo os vetores da base canônica, indicando a taxa de variação de acordo com cada variável; 3) Derivadas de ordem superior, como derivadas segundo as variáveis e mistas, utilizadas para analisar o comportamento local de uma função.

1. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
C´alculo Diferencial
An´alise Matem´atica 2/ C´alculo 2
2013/14 - Semestre de Ver˜ao
1/49

2. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Derivadas segundo um vetor
Defini¸c˜ao
Seja f : Df ⊂ Rn −→ R e a ∈ int(Df ) ent˜ao
fv (a) = lim
λ→0
f (a + λv) − f (a)
λ
representa a derivada de f segundo o vetor v no ponto a
(no caso do limite existir).
Nota: No caso em que v = 1 esta derivada chama-se
derivada direcional de f , segundo o vetor v no ponto a.
2/49

3. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Interpreta¸c˜oes:
fv (a) (com v = 1) indica o declive da recta tangente ao
gr´afico de f no ponto a que tem a dire¸c˜ao do vetor v.
fv (a) (com v = 1) indica a taxa de varia¸c˜ao, ou seja, a
quantidade de varia¸c˜ao por unidade na dire¸c˜ao de v, de f
no ponto a.
3/49

4. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
4/49

5. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f no ponto (a, b)
segundo o vetor (1, 0)? E (0, 1)?
5/49

6. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f no ponto (1, 1)
segundo o vetor (1, 0)?
6/49

7. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f no ponto (1, 1)
segundo o vetor (0, 1)?
7/49

8. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f nos pontos (−1, 1) e
(1, 1)segundo o vetor (1, 0)? E (0, 1)?
8/49

9. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f nos pontos (10, −5) e
(0, 0) segundo o vetor (1, 0)? E (0, 1)?
9/49

10. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Qual o sinal da derivada direcional de f em (10, −5) e (0, 5)
segundo o vetor (1, 0)? E (0, 1)?
10/49

11. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Calcule:
1 fv (a) para f (x, y) = x2y, v = (2, 1) e a = (1, 0).
2 a derivada direcional de f (x, y) = x2 sin(2y),segundo o
vetor v = (3, −4) no ponto a = (1, π
2 ).
3 a derivada de
f (x, y) =
xy
x+y se x + y = 0
x se x + y = 0
segundo os vetores v1 = (1, 1) e v2 = (1, −1) no ponto
a = (0, 0).
4 a derivada direcional de
f (x, y) =
2xy
x2+y2 se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
segundo o vetor v = (1, 1) no ponto a = (0, 0).
5 a derivada direcional de
f (x, y) =
y2 se x = 0
y2
x se x = 0
segundo os vetores v1 = (0, 2) e v2 = (1, 2) em a = (0, 0).
11/49

12. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
1 As figuras apresentam as linhas de n´ıvel de 3 fun¸c˜oes.
Qual o sinal das derivadas direcionais das fun¸c˜oes segundo
a dire¸c˜ao do vetor v = (1, 2) e w = (2, 1) nos pontos
marcados?
12/49

13. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Derivadas segundo um vetor para
fun¸c˜oes vetoriais
Defini¸c˜ao
Seja
f : Df ⊂ Rn −→ Rm
x −→ y = f (x) = (f1(x), ..., fm(x))
e a ∈ int(Df ) ent˜ao
fv (a) = f1v (a), ..., fmv (a)
representa a derivada de f segundo o vetor v no ponto a
(no caso dos limites existirem).
Nota: No caso em que v = 1 esta derivada chama-se
derivada direcional de f , segundo o vetor v no ponto a.
13/49

14. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
Calcule
1 fv (a) para
f (x, y, z) = (x − z, 2y)
com v = (1, 2, 0) e a = (1, 1, 1).
14/49

15. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Defini¸c˜ao
`As derivadas direcionais segundo os vetores da base can´onica
de Rn, chamam-se derivadas parciais.
No caso de n=2... os vetores da base can´onica s˜ao (1, 0) e
(0, 1)...
Chama-se derivada parcial em ordem a x a
∂f
∂x
(a, b) = lim
λ→0
f (a + λ, b) − f (a, b)
λ
(´e a derivada direcional segundo o vetor (1,0)).
Chama-se derivada parcial em ordem a y a
∂f
∂y
(a, b) = lim
λ→0
f (a, b + λ) − f (a, b)
λ
(´e a derivada direcional segundo o vetor (0,1)).
15/49

16. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Notas:
Para calcular a derivada (parcial) num ponto: se, na
vizinhan¸ca (bola) desse ponto a fun¸c˜ao est´a definida por:
apenas uma express˜ao: Regras de deriva¸c˜ao.
mais do que uma express˜ao: Defini¸c˜ao de derivada
parcial.
Interpreta¸c˜oes:
∂f
∂x (a, b) indica o declive da recta tangente ao gr´afico de f
no ponto (a, b) que ´e paralela ao eixo dos xx.
∂f
∂x (a, b) indica a taxa de varia¸c˜ao, ou seja, a quantidade
de varia¸c˜ao por unidade de x, de f no ponto (a, b).
16/49

17. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Sejam u = f (x), v = g(x), k ∈ R.
k = 0 (sin(u)) = cos(u)u
x = 1 (cos(u)) = − sin(u)u
(u + v) = u + v (tan(u)) = sec2(u)u
(ku) = ku (cot(u)) = − csc2(u)u
(u.v) = u v + uv (sec(u)) = sec(u) tan(u)u
u
v =
u v − uv
v2
(arcsin(u)) =
u
√
1 − u2
(uα) = αuα−1u , α ∈ Q {0} (arccos(u)) = −
u
√
1 − u2
√
u =
u
2
√
u
(arctan(u)) =
u
1 + u2
(ln(u)) =
u
u
(arccot(u)) = −
u
1 + u2
(eu) = euu (|u|) =
|u|
u
u =
u
|u|
u
(au) = au ln(a)u , a ∈ R {1} (cosh(u)) = sinh(u)u
(uv ) = uv ln(u)v + vuv−1u (sinh(u)) = cosh(u)u
17/49

18. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
Calcule
∂f
∂x (1, 2) e ∂f
∂y (1, 2) onde f (x, y) = x2y + 2exy .
as derivadas parciais de f (x, y, z) = ex z + x sin(zy) + zx.
∂f
∂x (1, 1), ∂f
∂y (1, 1), ∂f
∂x (0, 0) e ∂f
∂y (0, 0) onde
f (x, y) =
x3+y3
x2+y2 se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
as derivadas parciais de f nos pontos (0,2) e (0,0) onde:
f (x, y) =
4
x2+y2 se x2 + y2 > 4
ey−2 se x2 + y2 ≤ 4
18/49

19. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Derivadas de ordem superior `a
primeira
Derivadas de 2a ordem... de 3a ordem...
Derivadas quadradas:
∂2f
∂x2
=
∂
∂x
∂f
∂x
∂2f
∂y2
=
∂
∂y
∂f
∂y
Derivadas cruzadas:
∂2f
∂x∂y
=
∂
∂y
∂f
∂x
∂2f
∂y∂x
=
∂
∂x
∂f
∂y
19/49

20. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
1 Calcule as derivadas at´e `a 3a ordem das fun¸c˜oes:
1 f (x, y) = 5xy3
+ 2x2
y2
2 f (x, y) = sin(x)y5
2 Estude se para f (x, y) = 16 − x2 − y2 e
g(x, y) = x ln(x) + yex se tem que
∂f
∂x
(1, 1)
2
−
∂2g
∂x∂y
(1, 14) +
∂g
∂x
(1, 1) = 0.
3 Verifique que para g(x, y) = xye
x
y se tem que
x
∂3g
∂x3
+ y
∂3g
∂y∂x2
= 0
20/49

21. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Teorema de Schwarz:
Seja f : Df ⊂ R2 −→ R, e (a, b) ∈ intDf tal que
∂f
∂x , ∂f
∂y e ∂2f
∂x∂y existem numa vizinhan¸ca (bola) de (a, b);
∂2f
∂x∂y ´e cont´ınua em (a, b).
Ent˜ao
∂2f
∂y∂x
(a, b) =
∂2f
∂x∂y
(a, b).
21/49

22. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Defini¸c˜ao
Seja A um conjunto aberto contido no dom´ınio de f .
Uma fun¸c˜ao f diz-se de classe Ck (k ∈ N0) em A se e s´o se f
admite derivadas at´e `a ordem k (inclusive) em A cont´ınuas e
escreve-se
f ∈ Ck
(A)
22/49

23. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Fun¸c˜ao (definida em R2
)
diferenci´avel
Defini¸c˜ao (diferenci´avel)
Seja f : Df ⊂ R2 −→ R e (a, b) ∈ intDf .
Diz-se que f ´e diferenci´avel em (a, b) se existem as suas
derivadas parciais (em x e em y) neste ponto e se
lim
(h,k)→(0,0)
f (a + h, b + k) − f (a, b) − ∂f
∂x (a, b)h − ∂f
∂y (a, b)k
√
h2 + k2
= 0
23/49

24. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Proposi¸c˜ao:
Se f e g s˜ao fun¸c˜oes diferenci´aveis ent˜ao f + g, f − g, f × g,
f
g , (g(x) = 0, ∀x) e f ◦ g s˜ao diferenci´aveis.
Exemplos de fun¸c˜oes
DIFERENCI´AVEIS no seu dom. N˜AO DIFERENCI´AVEIS
• polin´omios • m´odulo (em 0)
• fun¸c. alg´ebricas • mantissa (n˜ao ´e cont´ınua)
• fun¸c. trigonom´etricas • por vezes as “uni˜oes” nas
• fun¸c. trigonom´etricas inversas fun¸c˜oes definidas por ramos
• fun¸c. logar´ıtmicas e exponenc. ...
...
24/49

25. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
Estude a diferenciabilidade das seguintes fun¸c˜oes nos pontos
indicados:
1 f (x, y) = x2 + y2 no ponto (1, 2).
2 Seja
f (x, y) =
√
xy se xy > 0
0 se xy ≤ 0
no ponto (0, 0).
3 Seja
f (x, y) =
x3
x2+y2 se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
no ponto (0, 0).
25/49

26. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Fun¸c˜ao escalar diferenci´avel
Defini¸c˜ao (diferenci´avel)
Seja f : Df ⊂ Rn −→ R e a ∈ intDf .
Diz-se que f ´e diferenci´avel em a se existem as suas derivadas
parciais neste ponto e se
lim
(h1,...,hn)→(0,...,0)
f (a + h) − f (a) − ∂f
∂x1
(a)h1 − ... − ∂f
∂xn
(a)hn
h2
1 + ... + h2
n
= 0
26/49

27. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Propriedades das fun¸c˜oes
diferenci´aveis
Seja f : D ⊂ Rn −→ R, a ∈ intDf .
f diferenci´avel em a ⇒ f cont´ınua em a.
f tem n − 1 der. parc. cont. em a
existem todas as der. parc. na B a
⇒ f dif. em a.
f ∈ C1(a) ⇒ f ´e diferenci´avel em a.
f ´e diferenci´avel em a ⇒ f admite derivada segundo
qualquer dire¸c˜ao em a.
ou seja,
f n˜ao ´e cont´ınua em a ⇒ f n ´e diferenci´avel em a.
f tem n − 1 der. parc. cont. em a
existem todas as der. parc. em a
⇒ f dif. em a.
f ∈ C1(a) ⇒ f ´e diferenci´avel em a.
f n˜ao admite derivada segundo alguma dire¸c˜ao em
a ⇒ f n˜ao ´e diferenci´avel em a.
27/49

28. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
Estude a diferenciabilidade das seguintes fun¸c˜oes nos pontos
indicados:
1 Seja
f (x, y) =
2x−3y
x+y se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
no ponto (0, 0).
2 Seja
f (x, y) =
x4
x2+y2 se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
no ponto (0, 0).
3 Seja
f (x, y) =
y3
x2+y2 se (x, y) = (0, 0)
0 se (x, y) = (0, 0)
no ponto (0, 0).
28/49

29. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Plano tangente
29/49

30. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Vamos procurar determinar o plano tangente ao gr´afico de
f : R2 −→ R no ponto (a, b).
Equa¸c˜ao do plano que passa no ponto (a, b, c):
A(x − a) + B(y − b) + C(z − c) = 0
Este plano vai passar no ponto (a, b, c) em que c = f (a, b), ou
seja,
A(x − a) + B(y − b) + C(z − f (a, b)) = 0
z − f (a, b) = −
A
C
(x − a) −
B
C
(y − b)
chamando λ1 = −A
C e λ2 = −B
C temos
z − f (a, b) = λ1(x − a) + λ2(y − b)
30/49

31. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Quando “cortamos” em y = b obtemos
z − f (a, b) = λ1(x − a)
que ´e a recta tangente ao gr´afico de f que ´e paralela ao eixo
dos xx’s, portanto o seu declive ´e ∂f
∂x (a, b) = λ1.
Analogamente, quando “cortamos” em x = a obtemos
z − f (a, b) = λ2(y − b)
que ´e a recta tangente ao gr´afico de f que ´e paralela ao eixo
dos yy’s, portanto o seu declive ´e ∂f
∂y (a, b) = λ2. Assim, a
equa¸c˜ao ´e
z − f (a, b) =
∂f
∂x
(a, b)(x − a) +
∂f
∂y
(a, b)(y − b)
31/49

32. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Resumindo:
A equa¸c˜ao do plano tangente ao gr´afico de f no ponto
(a, b, f (a, b)) ´e:
z − f (a, b) =
∂f
∂x
(a, b)(x − a) +
∂f
∂y
(a, b)(y − b)
Exerc´ıcio: Determine o plano tangente:
1 ao gr´afico da fun¸c˜ao f (x, y) = 2x2 + y2 em P=(1,1,3).
2 `a superf´ıcie de equa¸c˜ao z − 2x2 − 4y2 = 0 em P=(1,2,18).
3 `a superf´ıcie de equa¸c˜ao z = 1 − x2 em P=(0,0,1). (ver
fig.)
32/49

33. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Nota: Repare que se f ´e diferenci´avel no ponto (a, b)
lim
(h,k)→(0,0)
f (a + h, b + k) − f (a, b) − ∂f
∂x (a, b)h − ∂f
∂y (a, b)k
√
h2 + k2
= 0
como lim(h,k)→(0,0)
√
h2 + k2 = 0 tem-se que (ainda com
“mais for¸ca”)
lim
(h,k)→(0,0)
f (a + h, b + k) − f (a, b) −
∂f
∂x
(a, b)h −
∂f
∂y
(a, b)k = 0
donde, para h e k pequenos
f (a + h, b + k) − f (a, b) −
∂f
∂x
(a, b)h −
∂f
∂y
(a, b)k ≈ 0
ou seja:
f (a + h, b + k) ≈ f (a, b) +
∂f
∂x
(a, b)h +
∂f
∂y
(a, b)k
33/49

34. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
f (a + h, b + k) ≈ f (a, b) +
∂f
∂x
(a, b)h +
∂f
∂y
(a, b)k
fazendo x = a + h e y = b + k
tem-se, para (x, y) pr´oximos de (a, b), que
f (x, y) ≈ f (a, b) +
∂f
∂x
(a, b)(x − a) +
∂f
∂y
(a, b)(y − b)
Ou seja, f (x, y) ´e aproximadamente igual ao plano tangente
para (x, y) pr´oximos de (a, b).
Portanto podemos usar o plano tangente como uma
aproxima¸c˜ao (por um polin´omio de grau 1) ao gr´afico de f
numa vizinhan¸ca (bola) do ponto.
34/49

35. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Diferencial
Se f ´e diferenci´avel em (a, b)
f (x, y) − f (a, b) ≈
∂f
∂x
(a, b)(x − a) +
∂f
∂y
(a, b)(y − b)
∆f (a,b)→diferencial de f no ponto (a,b)
para x “pr´oximo” de a
e y “pr´oximo” de b.
35/49

36. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
36/49

37. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios
1 Calcule um valor aproximado de e1.1×0.9.
2 Calcule um valor aproximado de 9 × (1.95)2 + (8.01)2.
3 Seja g ∈ C1(R2) tal que
x=2.00 x=2.01
y=3.00 7.56 7.42
y=3.02 7.61
Calcule o valor em falta. (Sugest˜ao: use estimativas para
∂g
∂x (2, 3))
37/49

38. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
O gradiente
Defini¸c˜ao
Seja f : Df ⊂ Rn −→ R e a ∈ intDf . Define-se o gradiente de
f no ponto a por:
f (a) =
∂f
∂x1
(a), · · · ,
∂f
∂xn
(a)
Exerc´ıcio: Calcule f (1, 2) onde f (x, y) = y ln(x) + xy2.
http://www.slu.edu/classes/maymk/banchoff/GradientContours.html
38/49

39. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Aplica¸c˜ao do gradiente: derivada
segundo a dire¸c˜ao de v
Proposi¸c˜ao
Se f : Df ⊂ Rn −→ R ´e diferenci´avel em a ∈ int(D) e v ´e um
vetor de Rn ent˜ao a derivada de f segundo a dire¸c˜ao de v ´e
dada por
fv (a) = f (a)|v
onde | significa produto interno.
39/49

40. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios:
Calcule:
1 A derivada de f (x, y) = x2e−2y no ponto A = (2, 0),
segundo o vetor v = (1, 2).
2 A derivada direcional de f (x, y) = x3 + xy segundo o
vetor v = (1, 3) no ponto (1, 2).
3 A derivada de f (x, y) = 3x2 − 2y2 no ponto A = (−2, 1),
na dire¸c˜ao de P = −3
4, 0 para Q = (0, 1).
4 Determine a taxa de varia¸c˜ao de
f (x, y) = 2x2
+ 3xy − 2y2
no ponto (1, −2) na dire¸c˜ao do ponto dado `a origem.
40/49

41. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Nota: Se o vetor v ´e unit´ario (tem norma 1), a derivada
direcional de f no ponto a segundo a dire¸c˜ao do vetor u:
fu(a) = f (a)|u = f (a) u cos(θ) = f (a) cos(θ)
onde θ ´e o menor ˆangulo formado pelos vetores f (a) e u.
41/49

42. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Ent˜ao:
fu(a) ´e m´axima quando θ = 0, ou seja, quando f (a) e v
s˜ao dois vetores com a mesma dire¸c˜ao e sentido, e o seu
valor ´e f (a) . Assim a dire¸c˜ao de crescimento
m´aximo de f ´e dada por f (a).
fu(a) ´e m´ınima quando θ = π, ou seja, quando f (a) e v
s˜ao dois vetores com a mesma dire¸c˜ao e sentidos
contr´arios, e o seu valor ´e − f (a) . Assim a dire¸c˜ao
de crescimento m´ınimo (m´aximo negativo) de f ´e
dada por − f (a).
fu(a) ´e nula quando v e f (a) s˜ao perpendiculares.
Como sobre as linhas de n´ıvel fv (a) = 0 ent˜ao o vetor
gradiente ´e perpendicular `as linhas de n´ıvel.
42/49

43. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Em que dire¸c˜ao aponta o vetor gradiente nos pontos: (5, −5) e
(0, −5)? Verifique calculando.
43/49

44. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Em que dire¸c˜ao aponta o vetor gradiente nos pontos: (0, −5) e
(π
2 , −5)? Verifique calculando.
44/49

45. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Em que dire¸c˜ao aponta o vetor gradiente nos pontos: (1, 1)?
Verifique calculando.
45/49

46. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios I
1 Seja f (x, y) = 2x2y + exy uma fun¸c˜ao diferenci´avel no seu
dom´ınio.
1 Determine o gradiente de f no ponto (1,0) e represente-o
graficamente.
2 Calcule f(1,1)(1, 0).
3 Determinar um vetor unit´ario u de modo que
fu (−1, 0) = 1
2 .
4 Qual o valor m´aximo da derivada direcional de f no ponto
(1, 1)?
2 Considere o campo escalar f (x, y) = ex2+y − 2xy.
1 Calcule as fun¸c˜oes derivadas parciais de primeira ordem de
f e justifique que f ∈ C1
(R2
).
2 Determine os vetores segundo o qual a taxa de varia¸c˜ao de
f no ponto (1,-1) ´e nula.
46/49

47. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios II
3 Numa placa semi-circular x2 + y2 ≤ 4, com x ≥ 0 a
temperatura ´e dada pela lei
T(x, y) = 3yx2
− x3
+ 60
Determine um vetor no ponto P = (1, 1) tangente `a
isot´ermica que passa nesse ponto.
4 Considere o campo escalar definido em R2 por
f (x, y) = x2
e−2y
e o ponto P = (−2, 0). Determine
1 A dire¸c˜ao segundo a qual a fun¸c˜ao cresce mais
rapidamente em P.
2 O valor m´aximo da derivada direcional no ponto P.
3 A dire¸c˜ao segundo a qual fv (2, 0) = 0
47/49

48. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Exerc´ıcios III
5 Represente o vetor gradiente nalguns pontos.
48/49

49. AM2/C2
An´alise
Matem´atica
2/ C´alculo 2
Derivadas
direcionais
Derivadas
parciais
Derivadas de
ordem superior
T. Schwarz
Classe Ck
(A)
Diferenciabil.
Plano tang.
Diferencial
Gradiente
Autora:
Sandra Gaspar Martins
Com base no trabalho de:
Nuno David Lopes
e
Cristina Janu´ario
49/49