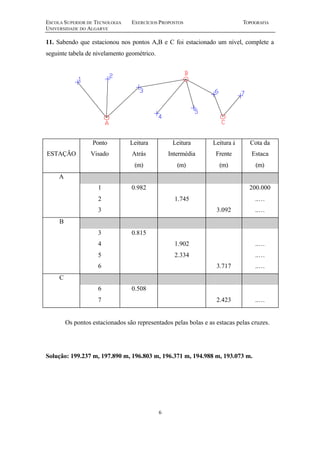
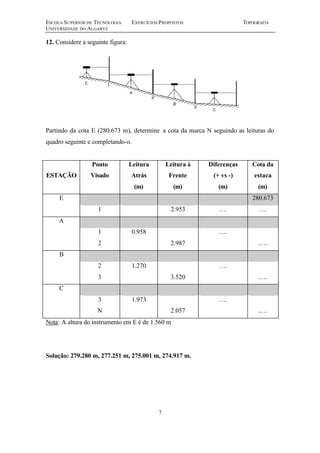
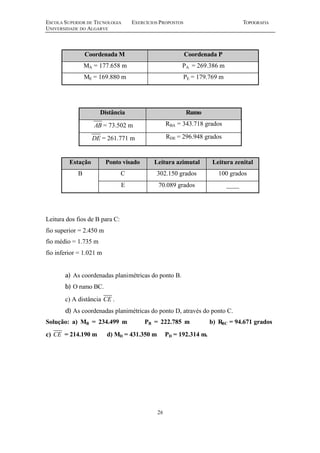
Este documento apresenta 15 exercícios de topografia sobre distâncias, escalas, altimetria, nivelamento, poligonais e coordenadas planas. Os exercícios envolvem cálculos trigonométricos e geométricos para resolver problemas topográficos como determinar distâncias, áreas, cotas e coordenadas de pontos.