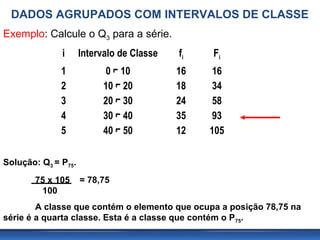
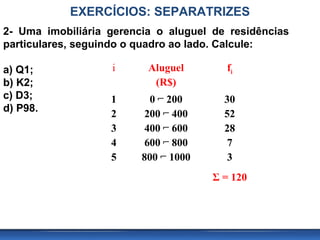
O documento aborda medidas separatrizes na estatística, explicando conceitos como mediana, quartis, quintis, decis e percentis, que dividem conjuntos de dados em partes iguais. São apresentados métodos para calcular essas medidas para dados agrupados e não agrupados, além de exemplos práticos. O texto inclui exercícios para fixação do conteúdo apresentado.

1. AULA 17
ESTATÍSTICA
Professor: João Alessandro
MEDIDAS SEPARATRIZES

2. MEDIDAS SEPARATRIZES
São números que dividem a seqüência ordenada
de dados em partes que contêm a mesma
quantidade de elementos da série.
Desta forma, a mediana que divide a
seqüência ordenada em dois grupos, cada um
deles contendo 50% dos valores da seqüência, é
também uma medida separatriz.
Além da mediana, as outras medidas
separatrizes que destacaremos são: quartis,
quintis, decis e percentis.

3. QUARTIS
Se dividirmos a série ordenada em quatro partes, cada uma
ficará com seus 25% de seus elementos.
Os elementos que separam estes grupos são chamados de
quartis.
Assim, o primeiro quartil, que indicaremos por Q1, separa a
seqüência ordenada deixando 25% de seus valores à esquerda e
75% de seus valores à direita.
O segundo quartil, que indicaremos por Q2, separa a seqüência
ordenada deixando 50% de seus valores à esquerda e 50% de seus
valores à direita.
Note que o Q2 é a Mediana da série.
O terceiro quartil Q3 obedece a mesma regra dos anteriores.
Q1 Q2 Q3 Q4
25% 25% 25% 25%

4. QUINTIS
Se dividirmos a série ordenada em cinco partes, cada
uma ficará com seus 20% de seus elementos.
Os elementos que separam estes grupos são
chamados de quintis.
Assim, o primeiro quintil, que indicaremos por K1,
separa a seqüência ordenada deixando 20% de seus valores
à esquerda e 80% de seus valores à direita.
De modo análogo são definidos os outros quintis.
Q1 Q2 Q3 Q4 Q5
20% 20% 20% 20% 20%

5. DECIS
Se dividirmos a série ordenada em dez partes, cada
uma ficará com seus 10% de seus elementos.
Os elementos que separam estes grupos são
chamados de decis.
Assim, o primeiro decil, que indicaremos por D1,
separa a seqüência ordenada deixando 10% de seus valores
à esquerda e 90% de seus valores à direita.
De modo análogo são definidos os outros decis.
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10
10% 10% 10% 10% 10% 10% 10% 10% 10% 10%

6. PERCENTIS
Se dividirmos a série ordenada em cem partes,
cada uma ficará com 1% de seus elementos.
Os elementos que separam estes grupos são
chamados de centis ou percentis.
Assim, o primeiro percentil, que indicaremos por
P1, separa a seqüência ordenada deixando 1% de seus
valores à esquerda e 99% de seus valores à direita.
De modo análogo são definidos os outros
percentis.
P1 P2 A P100
1% 99%

7. PERCENTIS
Se observarmos que os quartis, quintis e decis são
múltiplos dos percentis, então basta estabelecer a fórmula de
cálculo de percentis. Todas as outras medidas podem ser
identificadas como percentis. Ou seja:
QUARTIS- PERCENTIS QUINTIS-PERCENTIS DECIS - PERCENTIS
Q1 = P25 K1 = P20 D1 = P10
Q2 = P50 K2 = P40 D2 = P20
D3 = P30
Q3 = P75 K3 = P60
D4 = P40
K4 = P80 D5 = P50
D6 = P60
D7 = P70
D8 = P80
D9 = P90

8. DADOS NÃO-AGRUPADOS
Identificamos à medida que queremos obter com o percentil
correspondente, Pi.
Calculamos i% de n para localizar a posição do percentil i
no Rol, ou seja:
ixn
100
Em seguida, identificamos o elemento que ocupa esta
posição.
Note que se o elemento for um número inteiro, então Pi que
estamos procurando identificar é um dos elementos da seqüência
ordenada.
Se não for um número inteiro, isto significa que Pi é um
elemento intermediário entre os elementos que ocupam as
posições aproximadas por falta ou por excesso do valor calculado.
Neste caso, Pi é definido como sendo a média dos valores que
ocupam estas posições aproximadas.

9. DADOS NÃO-AGRUPADOS - EXEMPLOS
Dada a série de valores, Calcule Q1
1, 2, 5, 5, 5, 8, 10, 11, 12, 12, 13, 15.
Solução: Q1 = P25.
Calculamos 25% de 12 que é o número de elementos da série
obtendo:
25 x 12 =3
100
Este valor indica a posição do P25 no Rol, isto é, o P25 é o
terceiro elemento do Rol. Observando o terceiro elemento do Rol
obtém-se 5.
Portanto Q1 = P25 = 5.
Interpretação: 25% dos valores desta seqüência são valores
menores que 5 e 75% dos valores desta seqüência são valores
maiores que 5.

10. DADOS AGRUPADOS SEM INTERVALOS DE CLASSE
Identificamos à medida que queremos obter com o
percentil correspondente, Pi.
Calculamos i% de n(Σfi) para localizar a posição do
percentil i no Rol, ou seja:
i x Σfi
100
Exemplo: Calcule o D4 para a série
xi fi Fi
2 3 3
4 5 8
5 8 16
7 6 22
10 2 24
Σfi = 24

11. DADOS AGRUPADOS SEM INTERVALOS DE CLASSE
xi fi Fi Solução: D4 = P40.
2 3 3 Calculamos 40% de 24 que é o
4 5 8 número de elementos da série
5 8 16 obtendo:
7 6 22 40 x 24 = 9,6
10 2 24 100
Σfi = 24 Este valor indica a
posição do P40 é um valor
compreendido entre o nono e o
décimo elemento da série.
Observamos que o nono e o décimo elementos é o número 5. Assim:
D4 = 5
Interpretação: 40% dos valores desta seqüência são valores menores
ou iguais que 5 e 60% dos valores desta seqüência são valores
maiores ou iguais que 5.

12. DADOS AGRUPADOS COM INTERVALOS DE CLASSE
Para obtermos a fórmula geral para o cálculo dos percentis,
vamos generalizar a fórmula de mediana:
i x n - F(ant) x h
Pi = li + 100
fi
Sendo:
Pi – Percentil i (1, 2, 3, ..., 99);
li - limite inferior da classe que contém o percentil;
n – número de elementos da série (Σfi);
F(ant) – freqüência acumulada da classe anterior à classe
que contém o percentil;
fi - freqüência simples da classe que contém o percentil;
h - amplitude do intervalo da classe mediana

13. DADOS AGRUPADOS COM INTERVALOS DE CLASSE
Exemplo: Calcule o Q3 para a série.
i Intervalo de Classe fi Fi
1 0 ⌐ 10 16 16
2 10 ⌐ 20 18 34
3 20 ⌐ 30 24 58
4 30 ⌐ 40 35 93
5 40 ⌐ 50 12 105
Solução: Q3 = P75.
75 x 105 = 78,75
100
A classe que contém o elemento que ocupa a posição 78,75 na
série é a quarta classe. Esta é a classe que contém o P75.

14. DADOS AGRUPADOS COM INTERVALOS DE CLASSE
Substituindo os valores na fórmula obtém-se:
75 x 105 - 58 x 10
P75 = 30 + 100 = 35,93
35
Portanto Q3 = P75 = 35,93.
Interpretação: 75% dos valores desta seqüência são
valores menores ou iguais a 35,93 e 25% dos valores
desta seqüência são valores maiores ou iguais que
35.93.

15. EXERCÍCIOS: SEPARATRIZES
1- Se uma série ordenada possui 180 elementos, dê o
número aproximado de elementos que situam:
a) Acima do P20;
b) Abaixo do K3;
c) Acima do Q3;
d) Abaixo do P90;
e) Entre o P10 e o P90;
f) Entre o Q1 e o Q3;
g) Entre o Q3 e o P80.

16. EXERCÍCIOS: SEPARATRIZES
2- Uma imobiliária gerencia o aluguel de residências
particulares, seguindo o quadro ao lado. Calcule:
a) Q1; i Aluguel fi
b) K2; (R$)
c) D3; 1 0 ⌐ 200 30
d) P98.
2 200 ⌐ 400 52
3 400 ⌐ 600 28
4 600 ⌐ 800 7
5 800 ⌐ 1000 3
Σ = 120

17. EXERCÍCIOS: SEPARATRIZES
i Consumo fi 3- A distribuição de valores
por nota de 54 notas fiscais emitidas
(R$)
na mesma data,
1 0 ⌐ 50 10 selecionadas em uma loja
2 50 ⌐ 100 28 de departamentos. Calcule:
3 100 ⌐ 150 12
4 150 ⌐ 200 2
a) Q3;
5 200 ⌐ 250 1
b) K4;
6 250 ⌐ 300 1
c) D7;
Σ = 54 d) P75.

18. EXERCÍCIOS: SEPARATRIZES
4 - Tomando como base o exercício anterior, o gerente
desta loja decidiu premiar a nível promocional com um
brinde diário, 10% dos fregueses que mais consumirem,
nos próximos 30 dias. A partir de qual valor de consumo
da nota fiscal os clientes seriam premiados?

19. EXERCÍCIOS: SEPARATRIZES
i Preço fi 5- A tabela ao lado
unitário (R$) representa a venda de livros
1 0 ⌐ 10 4.000 didáticos em uma editora na
2 10 ⌐ 20 13.500 primeira semana de março.
3 20 ⌐ 30 25.600 Calcule:
4 30 ⌐ 40 43.240
a) Q1;
5 40 ⌐ 50 26.800
b) Q3;
6 50 ⌐ 60 1.750
c) P90;
Σ = 54 d) P10.

20. DÚVIDAS?
joao.alessandro@grupointegrado.br
jalmat@hotmail.com