Este documento apresenta conceitos fundamentais sobre curvas paramétricas em R2 e R3, incluindo: 1) Definição de curvas paramétricas através de funções vetoriais; 2) Exemplos de representação geométrica de várias curvas; 3) Noção de orientação, origem e extremidade de uma curva.

1. AM2
Linha
Vector
tangente e
recta tangente
Comprimento
Integrais de Linha
de uma linha
An´lise Matem´tica 2
a a
Integral de
linha de
campo escalar
Sandra Gaspar Martins
sandra.martins@adm.isel.pt
2o Semestre 2011/12
vers˜o de 16 de Maio de 2012
a
1/24

2. AM2 Quais destas linhas s˜o gr´ficos de fun¸˜es?
a a co
(Cada objecto tem uma s´ imagem.)
o
Linha
Vector
tangente e
recta tangente
Comprimento
de uma linha
Integral de
linha de
campo escalar
2/24

3. AM2
Equa¸oes param´tricas da curva C
c˜ e
Linha de R2
Vector
tangente e
recta tangente
Defini¸˜o
ca
Comprimento Seja C uma curva/linha de R2 tal que
de uma linha
Integral de
linha de x = f (t)
campo escalar , t ∈ I = [a, b] ⊂ R,
y = g (t)
com f e g fun¸˜es cont´
co ınuas em I. A t chama-se a vari´vel ou
a
parˆmetro.
a
A orienta¸˜o da curva C corresponde ao sentido definido pelos
ca
valores crescentes de t no intervalo I .
Ao ponto (x, y ) correspondente a t = 0 chama-se origem ou
ponto de partida e ao correspondente a t = b chama-se
extremidade ou ponto de chegada da curva.
2/24

4. AM2 Outra forma de descrever a curva C ´ utilizando fun¸˜es
e co
vectoriais:
Linha
r : I = [a, b] −→ R2
Vector
tangente e t −→ r (t) = (f (t), g (t))
recta tangente
Comprimento
r (a) ´ a origem ou ponto de partida e
e
de uma linha r (b) ´ a extremidade ou ponto de chegada de C.
e
Integral de
linha de
campo escalar
Exemplo: Represente geometricamente a curva C:
r : [−1, 1] −→ R2
t −→ r (t) = (t, t 2 )
ou seja,
x =t
, t ∈ I = [−1, 1]
y = t2
ou seja,
r (t) = (t, t 2 ), t ∈ [−1, 1] 3/24

5. AM2
Exerc´
ıcios
Linha
Vector
tangente e
recta tangente
Represente geometricamente as curvas:
Comprimento
de uma linha
1 r (t) = (t, t 2 ), t ∈ [0, 2]
Integral de 2 r (t) = (t, sin(t)), t ∈ [0, π]
linha de √
campo escalar 3 r (t) = (t, t), t ∈ [0, 9]
4 r (t) = (t, t + 3), t ∈ [0, 5]
5 r (t) = (t, t), t ∈ [0, 2]
6 r (t) = (t, −t), t ∈ [0, 2]
7 r (t) = (1 + 2t, 2 + t), t ∈ [0, 1]
8 r (t) = (t − 1, 3t + 2), t ∈ [0, 2]
9 r (t) = (t + 1, t 2 + 3), t ∈ [0, 2]
4/24

6. AM2
Exerc´
ıcios
Linha
Vector
tangente e
recta tangente
Represente geometricamente as curvas:
Comprimento
de uma linha
1 r (t) = (3 cos(t), 3 sin(t)), t ∈ [0, 2π]
Integral de 2 r (t) = (2 cos(t), 4 sin(t)), t ∈ [0, π]
linha de
campo escalar 3 r (t) = (cos(t) − 2, sin(t) + 3), t ∈ [0, π ]
2
4 r (t) = (sin(t), cos(t)), t ∈ [0, 2π]
5 r (t) = (5 cos(t), 4 sin(t)), t ∈ [π, 2π]
6 r (t) = (cos(t), sin(t)), t ∈ [−π, π ]
3
7 r (t) = (cos(t) − 4, sin(t) + 2), t ∈ [− π , 0]
2
8 r (t) = (2 sin(t), 2 cos(t)), t ∈ [0, π]
9 r (t) = (sin(t) − 1, cos(t) + 3), t ∈ [ π , 2π]
2
5/24

7. AM2
Defini¸˜o
ca
Linha
Uma parametriza¸˜o de um segmento de recta com origem
ca
Vector
em A e extremidade em B, pode ser:
tangente e
recta tangente
Comprimento r (t) = A + t(AB), t ∈ [0, 1].
de uma linha
Integral de
linha de Defini¸˜o
ca
campo escalar
Seja C uma curva dada pelo caminho r (t), t ∈ [a, b] com
origem em A = r (A) e extremidade em B = r (B). A curva −C
(com origem em B e extremidade em A) ´ dada pelo caminho
e
inverso de r , r ∗ , obt´m-se se r substituindo t por −t, ou seja,
e
r ∗ (t) = r (−t), t ∈ [−b, −a]
.
Exemplo: Parametrize o segmento de recta de R2 que come¸a
c
em (0,1) e termina em (2,3) e o caminho inverso.
6/24

8. AM2
Exerc´
ıcios I
Linha
Vector
tangente e
recta tangente
Comprimento
de uma linha Parametrize as seguintes curvas e as curvas inversas:
Integral de
linha de
1 O segmento de recta que come¸a em (1,2) e termina em
c
campo escalar
(-1,-3).
2 A parte da recta y = 2x para x ∈ [−2, 3].
2
3 A parte do gr´fico da fun¸˜o f (x) = e x − 1 para
a ca
x ∈ [0, 1].
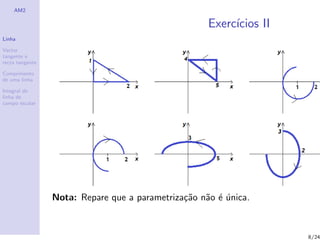
4 As linhas que se seguem:
7/24

9. AM2
Exerc´
ıcios II
Linha
Vector
tangente e
recta tangente
Comprimento
de uma linha
Integral de
linha de
campo escalar
Nota: Repare que a parametriza¸˜o n˜o ´ unica.
ca a e ´
8/24

10. AM2
Equa¸oes param´tricas da curva C
c˜ e
Linha de R3
Vector
tangente e
recta tangente Defini¸˜o
ca
Comprimento
de uma linha Seja C uma curva/linha de R3 tal que
Integral de 
linha de
campo escalar  x = f (t)
y = g (t) , t ∈ I = [a, b] ⊂ R,
z = h(t)

ou seja,
r : I = [a, b] −→ R3
t −→ r (t) = (f (t), g (t), h(t))
ou seja,
r (t) = (f (t), g (t), h(t)), t ∈ [a, b]
9/24

11. AM2
Exerc´
ıcios
Linha
Vector
tangente e
recta tangente
Represente geometricamente as curvas:
Comprimento
de uma linha
1 r (t) = (0, 2, 2t), t ∈ [−1, 1]
Integral de
linha de
campo escalar
2 r (t) = (0, t, 2t + 1), t ∈ [0, 3]
3 r (t) = (t, 5, t − 3), t ∈ [−2, 2]
4 r (t) = (cos(t), sin(t), 2), t ∈ [0, 2π]
5 H´lice circular:
e
r (t) = (cos(t), sin(t), t), t ∈ [0, 4π]
6 H´lice el´
e ıptica:
r (t) = (2 cos(t), 3 sin(t), t), t ∈ [0, 4π]
10/24

12. AM2
Exerc´
ıcios
Linha
Vector Parametrize as linhas de R3 indicadas na figura seguinte que
tangente e
recta tangente representa o cilindro
Comprimento
de uma linha
{(x, y , z) ∈ R3 : x 2 + y 2 = 9, 0 ≤ z ≤ 5}
Integral de
linha de
campo escalar
11/24

13. AM2
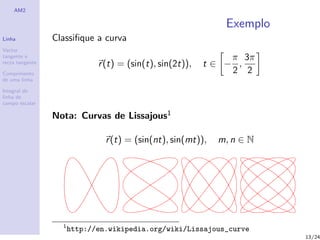
Classifica¸˜o de curvas
ca
Linha
Vector
tangente e Defini¸˜o
ca
recta tangente
Seja C uma curva dada por r (t), t ∈ [a, b].
Comprimento
de uma linha A curva C diz-se fechada se a origem coincide com a
Integral de
linha de
extremidade, ou seja, r (a) = r (b). Caso contr´rio a curva
a
campo escalar diz-se aberta.
A curva C diz-se simples se n˜o se intersecta a si pr´pria
a o
(excluindo a origem e a extremidade).
12/24

14. AM2
Exemplo
Linha Classifique a curva
Vector
tangente e π 3π
recta tangente r (t) = (sin(t), sin(2t)), t∈ − ,
Comprimento 2 2
de uma linha
Integral de
linha de
campo escalar
Nota: Curvas de Lissajous1
r (t) = (sin(nt), sin(mt)), m, n ∈ N
1
http://en.wikipedia.org/wiki/Lissajous_curve
13/24

15. AM2
Vector tangente e recta tangente
Linha
Vector
tangente e Defini¸˜o
ca
recta tangente
Comprimento
Seja C uma curva de Rn dada por r (t), t ∈ [a, b].
de uma linha Designa-se por vector tangente ` curva C no ponto
a
Integral de
linha de
P0 = r (t0 ) a derivada
campo escalar
r (t0 + h) − r (t0 )
r (t0 ) = lim , t0 ∈]a, b[
h→0 h
quando existe e ´ n˜o nula.
e a
A recta tangente ` curva em P0 = r (t0 ) ´ dada por:
a e
rT (t) = r (t0 ) + tr (t0 ), t∈R
14/24

16. AM2
1 Considere o caminho, r (t), que leva de A = (1, 0) para
B = (−1, 0), ao longo de uma circunferˆncia de equa¸˜o
e ca
Linha
Vector
x2 + y2 = 1
tangente e
recta tangente
em sentido directo (anti-hor´rio). Determine a equa¸˜o da
a ca
Comprimento
de uma linha recta tangente ` curva no ponto (0,1).
a
Integral de
linha de
2 Considere o caminho, r (t), que leva de A = (1, 0) para
campo escalar B = (0, 2), ao longo de uma elipse de equa¸˜o
ca
y2
x2 + =1
4
em sentido directo (anti-hor´rio). Determine a equa¸˜o da
a ca
recta tangente ` curva no ponto correspondente a t = π .
a 4
3 Determine a recta tangente ` curva representada pela
a
fun¸˜o
ca
r (t) = (2 cos(t), 2 sin(t), t)
no ponto t0 = π .
4
15/24

17. AM2
Defini¸˜o
ca
Linha Uma curva C de Rn dada por r (t), t ∈ [a, b] diz-se regular
Vector se a derivada r (t) existe e ´ cont´
e ınua (o que significa que
tangente e
recta tangente r (t) ∈ C 1 ) e n˜o nula em ]a, b[.
a
Comprimento
de uma linha
C ´ seccionalmente regular se se puder dividir num n´mero
e u
Integral de
linha de finito de curvas regulares.
campo escalar
Nota: Se um caminho ´ regular, a curva por ele descrita n˜o
e a
apresenta bicos nem esquinas angulosas pois a derivada evolui
sem varia¸˜es bruscas de direc¸˜o ou sentido.
co ca
16/24

18. AM2
Aplica¸oes
c˜
Linha
Se r (t) der origem a uma curva que traduz o movimento de
Vector
tangente e um corpo ou part´ ıcula, r (t) corresponder´ ao vector
a
recta tangente
velocidade, ou seja,
Comprimento
de uma linha
Integral de
linha de
v (t) = r (t).
campo escalar
O vector acelera¸˜o ser´
ca a
a(t) = v (t) = r (t).
Exemplo: Considere um objecto que se move ao longo de uma
curva C dada por
r (t) = (t − 2, t 2 ).
Determine os vectores velocidade e acelera¸˜o nos instantes
ca
t = 0 e t = 1. Represente-os.
17/24

19. AM2
Comprimento de uma linha
Linha
Vector
tangente e
recta tangente Defini¸˜o
ca
Comprimento
de uma linha
Seja C uma curva dada por r (t), t ∈ [a, b].
Integral de
Chamamos comprimento da linha/curva C com origem em
linha de
campo escalar
A = r (a) e extremidade B = r (b) ao integral
b
lC = r (t) dt
a
Defini¸˜o
ca
Uma curva diz-se rectific´vel se tiver comprimento finito.
a
18/24

20. AM2
Exerc´
ıcios
Linha 1 Prove que o per´
ımetro de uma circunferˆncia de raio R ´
e e
Vector
tangente e
2πR.
recta tangente 2 Determine k de modo que o comprimento da recta
Comprimento
de uma linha y = −2x + 1 entre 0 e k seja 2.
Integral de
3 Considere
linha de
campo escalar r (t) = 4 sin(t)e1 + 3t e2 + 4 cos(t)e3 , t ∈ [0, π]
Esboce a curva e calcule o seu comprimento. (R : 5π)
4 Determine o comprimento da curva C de equa¸˜es
co
param´tricas
e
x = e t cos(t) π
, t ∈ 0,
y = e t sin(t) 2
5 Determine o comprimento do arco de curva dado por
 x = ae t cos(t)

y = ae t sin(t)
z = ae t

√ 19/24

21. AM2
Defini¸˜o
ca
Seja C uma curva dada por r (t), t ∈ [a, b].
Linha Seja f : Df ⊂ Rn −→ R um campo escalar cont´ ınuo cujo
Vector
tangente e
dom´ Df cont´m todos os pontos da curva C
ınio e
recta tangente Chamamos integral de linha do campo escalar f ao longo da
Comprimento
de uma linha
curva C ao integral
Integral de b
linha de
campo escalar f dS = f (r (t)) r (t) dt
C a
Notas:
S ´ o comprimento infinit´simo do arco, ou seja,
e e
dS
S= r (t) dt logo dt = r (t) portanto
dS = r (t) dt
Quando a curva ´ fechada o integral de linha representa-se
e
por
f dS
C
e designa-se por circula¸˜o.
ca
Este integral n˜o depende da parametriza¸˜o escolhida
a ca 20/24

22. AM2
Propriedades
Linha
Vector
tangente e
recta tangente Propriedades dos integrais de linha de campos escalares:
Comprimento
de uma linha
Seja f e g campos escalares cont´ınuos com Df , Dg ⊂ Rn e
Integral de
C curva regular totalmente contida em Df ∩ Dg .
linha de
campo escalar
C1 e C2 curvas regulares totalmente contidas em Df .
α, β ∈ R.
1
αf + βg dS = α f dS + β g dS
C C C
2
f dS = 1f dS + 2f dS
C1 ∪C2 C C
21/24

23. AM2
Exerc´
ıcios I
Linha
Vector
tangente e
1 Calcule C f dS onde C ´ a linha da figura:
e
recta tangente
Comprimento
de uma linha
Integral de
linha de
campo escalar
2 Calcule C y dS onde C ´ a meia circunferˆncia de raio 2
e e
centrada na origem percorrida desde o ponto (2,0) at´ ao
e
ponto (-2,0). (R: 8)
√
3 Calcule C 2 x − y dS onde C ´ o semento de recta com
e
√
origem em (0,0) e extremidade em (1,1). (R: 5 6 2 )
4 Calcule C x + z dS onde C ´ o segmento de recta que tem
e
√
origem em (0,2,3) e termina em (2,1,0). (R: 5 14
2 )
22/24

24. AM2
Exerc´
ıcios II
Linha
Vector
tangente e
recta tangente
Comprimento
de uma linha 5 Calcule C x + y + z dS onde C ´ a linha de equa¸˜o
e ca
Integral de
linha de param´trica
e 
campo escalar
 x = cos(t)
y = sin(t)
z =t

entre os pontos (1,0,0) e (1,0,2π).
23/24

25. AM2
Linha
Vector
tangente e
recta tangente
Comprimento
de uma linha
Integral de
linha de
campo escalar
Autora:
Sandra Gaspar Martins
Com base no trabalho de:
Nuno David Lopes
e
Cristina Janu´rio
a
24/24