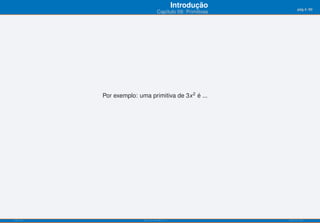
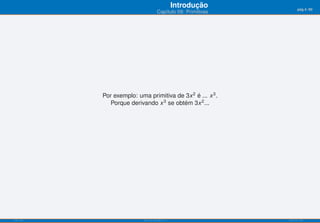
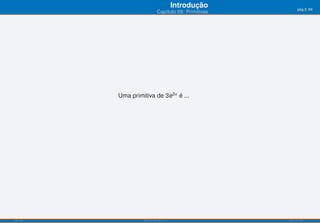
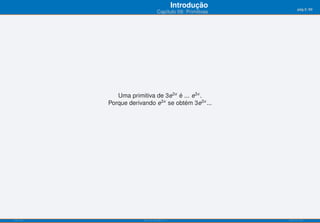
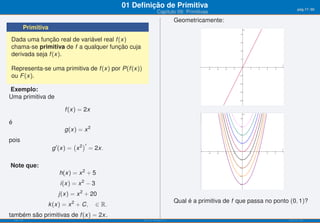
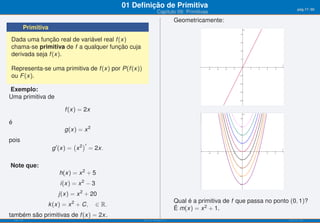
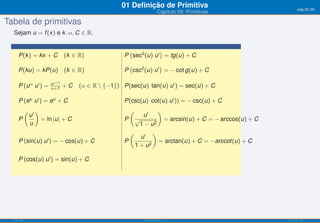
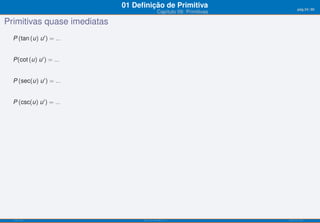
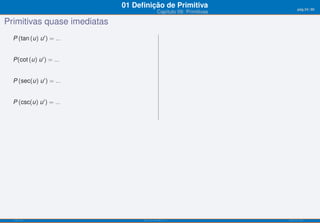
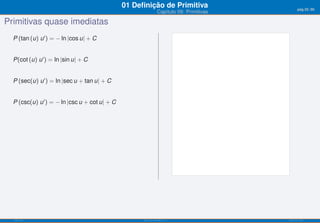
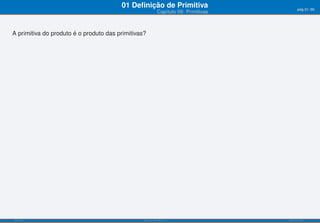
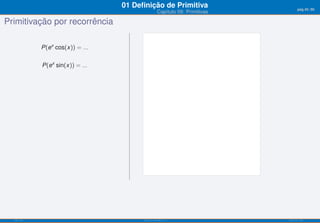
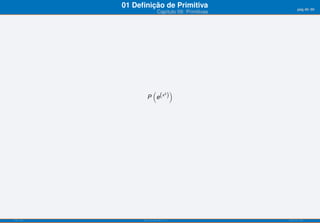
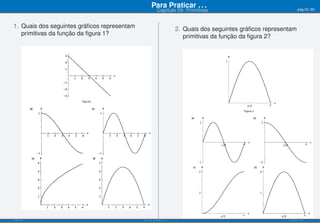
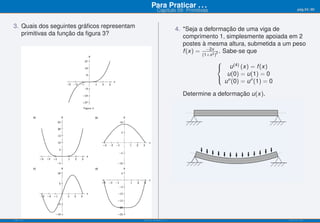
O documento apresenta o capítulo 09 sobre primitivas. Introduz o conceito de primitiva como a função cuja derivada é igual a uma dada função. Fornece exemplos de primitivas imediatas e explica que existem várias funções que podem ser primitivas da mesma função. Apresenta ainda objetivos de aprendizagem e uma tabela resumindo fórmulas para calcular primitivas de funções elementares.




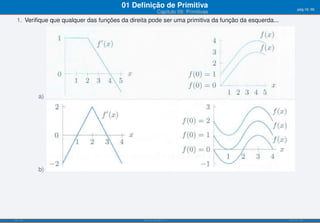














![Para Praticar . . . pág.55/90
Capítulo 09: Primitivas
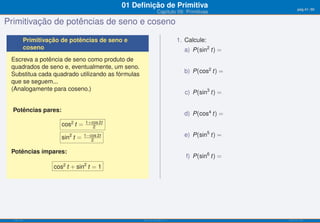
5. Considere um veículo que tem o seguinte 6. Considerando que a aceleração da força
comportamento de aceleração (m/s2 ) em gravítica é 9, 8m/s2 , e desprezando a
recta: resistência do ar, determine quanto tempo
⎧ √ demora uma massa a chegar ao chão, se for
12 t t ∈ [0, 1]
largada do topo de um prédio de 98m.
⎨
2
a(t) = 12 − 6(t − 1) t ∈]1, 2]
96
t ∈]2, +∞[
⎩
(t+2)2
a) Determine aproximadamente o tempo
necessário para o veículo atingir a
velocidade de 100km/h(≈ 28m/s).
b) Qual a velocidade máxima do veículo?
ISEL-IPL Análise Matemática 1 UIED-FCT-UNL](https://image.slidesharecdn.com/cap09-primitivas2-120702125504-phpapp01/85/Cap09-primitivas2-67-320.jpg)