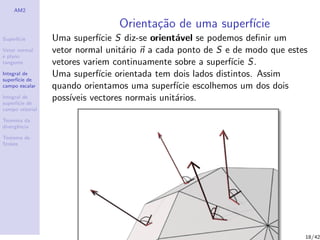
O documento aborda conceitos de superfícies em cálculo, incluindo a definição de parametrização, vetores normais, planos tangentes e integrais de superfícies de campos escalares e vetoriais. Ele também apresenta teoremas como o teorema da divergência e o teorema de Stokes, além de exercícios para aplicação prática dos conceitos discutidos. Há uma ênfase na parametrização de superfícies usando diferentes coordenadas e na determinação de equações relacionadas a superfícies específicas.

1. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Integrais de Superf´ıcie
An´alise Matem´atica 2/ C´alculo 2
2o Semestre 2013/14
vers˜ao de 5 de Junho de 2014
1/42

2. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Defini¸c˜ao
Chama-se parametriza¸c˜ao de uma superf´ıcie a uma aplica¸c˜ao:
R : ¯D ⊂ R2 −→ R3
(u, v) −→ (x(u, v), y(u, v), z(u, v))
com D um aberto conexo de R2.
2/42

3. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios I
Parametrize as superf´ıcies usando, se poss´ıvel, as projec¸c˜oes em
xOy, yOz e em xOz:
1
S = (x, y, z) ∈ R3
: x2
+ y2
= z, z ≤ 4
2
S = (x, y, z) ∈ R3
: x2
+ y2
= z2
, 1 ≤ z ≤ 4
3
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 9, z ≥ 0
4 *
S = (x, y, z) ∈ R3
: x2
+ y2
= 16, −1 ≤ z ≤ 3
3/42

4. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios II
5
S = (x, y, z) ∈ R3
: z = 1 − x2
, z ≥ 0, 0 ≤ y ≤ 3
6
S = (x, y, z) ∈ R3
: x + y + x = 1, x ≥ 0, y ≥ 0, z ≥ 0
7
S = (x, y, z) ∈ R3
: z = 1, x2
+ y2
≤ 4
8
S = (x, y, z) ∈ R3
: x = y, −1 ≤ z ≤ 3, 0 ≤ x ≤ 2
4/42

5. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios III
Parametrize as superf´ıcies usando coordenadas polares:
1
S = (x, y, z) ∈ R3
: x2
+ y2
= z, z ≤ 9
2
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 1, z ≤ 0
3
S = (x, y, z) ∈ R3
: x2
+ y2
= z2
, −3 ≤ z ≤ 0
4 *
S = (x, y, z) ∈ R3
: x2
+ y2
= 4, −1 ≤ z ≤ 4
5/42

6. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Qual o tipo de deforma¸c˜ao que ´e produzida pela parametriza¸c˜ao
em coordenadas polares e em coordenadas cartesianas?
6/42

7. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios IV
Parametrize as superf´ıcies:
1
S = (x, y, z) ∈ R3
: x2
+ y2
= 9 − z, 0 ≤ z < 5, x ≤ 0
2
S = (x, y, z) ∈ R3
: x2
+ y2
= z2
, −4 ≤ z ≤ 0, y ≤ x, x ≥ 0
3
S = (x, y, z) ∈ R3
: x2
+ y2
= 4, −2 ≤ z ≤ 3, y ≤ 0
4
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 9, x ≤ 0, y ≤ 0, z ≤ 0
7/42

8. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios V
Parametrize as superf´ıcies:
1
S = (x, y, z) ∈ R3
: (x − 2)2
+ (y + 1)2
= 9 − z, z ≥ 0
2
S = (x, y, z) ∈ R3
: y2
+ z2
= x2
, −4 ≤ x ≤ 0, z ≥ 0
3
S = (x, y, z) ∈ R3
:
x
3
2
+ y2
= 4, −1 ≤ z ≤ 5, y ≤ 0
4
S = (x, y, z) ∈ R3
: (x − 3)2
+
z
2
2
= y, x ≤ 3, y ≤ 4
8/42

9. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios VI
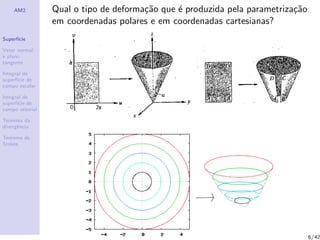
Parametrize, usando coordenadas esf´ericas, as superf´ıcies:
1
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 9, x ≤ 0, y ≤ 0, z ≤ 0
2
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 4, x ≥ 0, y ≥ 0, z ≤ 0
3
S = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 25, x ≥ 0, y ≤ 0, z ≤ 0
Coordenadas esf´ericas



x = ρ cos(θ) sin(ϕ)
y = ρ sin(θ) sin(ϕ)
z = ρ cos(ϕ)
, θ ∈ [0, 2π[, ϕ ∈ [0, π], ρ ∈ R+
9/42

10. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Seja S uma superf´ıcie parametrizada por
r(u, v) = (x(u, v), y(u, v), z(u, v)), (u, v) ∈ D
de classe C1(D).
∂r
∂u
(a, b, c)
´e um vetor tangente `a superf´ıcie S no ponto (a, b, c) .
∂r
∂v
(a, b, c)
´e um vetor tangente `a superf´ıcie S no ponto (a, b, c) .
10/42

11. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Vetor normal
Seja S uma superf´ıcie parametrizada por
r(u, v) = (x(u, v), y(u, v), z(u, v)), (u, v) ∈ D
de classe C1(D).
Um vetor normal `a superf´ıcie num ponto
P = (a, b, c) = (x(u0, v0), y(u0, v0), z(u0, v0)) ´e dado por
∂r
∂u
(u0, v0) ×
∂r
∂v
(u0, v0) =
e1 e2 e3
∂x
∂u
∂y
∂u
∂z
∂u
∂x
∂v
∂y
∂v
∂z
∂v
=
∂y
∂u
∂z
∂v
−
∂z
∂u
∂y
∂v
e1+
∂z
∂u
∂x
∂v
−
∂x
∂u
∂z
∂v
e2+
∂x
∂u
∂y
∂v
−
∂y
∂u
∂x
∂v
(desde que seja n˜ao nulo.) Ao vetor anterior chama-se vetor
produto fundamental.
11/42

12. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Notas:
1 n =
∂r
∂u
× ∂r
∂v
∂r
∂u
× ∂r
∂v
´e normal `a superf´ıcie e unit´ario.
2 O vetor ∂r
∂v × ∂r
∂u tamb´em ´e normal a S mas tem sentido
oposto a ∂r
∂u × ∂r
∂v .
3 Uma superf´ıcie com vetor normal (n˜ao nulo) em todos os
pontos diz-se regular (n˜ao apresenta regi˜oes pontiagudas).
4 Equa¸c˜ao cartesiana do plano que passa no ponto (a, b, c)
e ´e normal ao vetor n = (n1, n2, n3):
n1(x − a) + n2(y − b) + n3(z − c) = 0
12/42

13. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios
1 Determine a equa¸c˜ao do plano tangente ao parabol´oide
parametrizado por
r(u, v) = (u, v, u2
+ v2
)
no ponto (1, 2, 5).
2 Determine as equa¸c˜oes dos planos tangentes ao
parabol´oide dado pela equa¸c˜ao
x2
+ y2
= 4 − z
nos pontos (0,0,4) e (-1,1,2).
13/42

14. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Defini¸c˜ao (Integral de superf´ıcie de campo escalar)
Seja S ≡ r(D) uma superf´ıcie, r ∈ C1(D) e f : Ω −→ R um
campo escalar limitado com S ⊂ Ω.
Define-se o integral de superf´ıcie de f sobre S como:
S
f dS =
D
f (r(u, v))
∂r
∂u
×
∂r
∂v
(u, v) dudv
Nota:
´area de S =
S
1 dS
14/42

15. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Proposi¸c˜ao
O integral de superf´ıcie de campo escalar n˜ao depende da
parametriza¸c˜ao.
Se S e S1 s˜ao duas superf´ıcies que apenas diferem num
n´umero finito de linhas, ent˜ao:
S
f dS =
S1
f dS
Interpreta¸c˜ao:
S f dS d´a a quantidade total de f sobre a superf´ıcie S.
Por exemplo, se f (x, y, z) indicar a quantidade de humidade
em cada ponto (x,y,z), este integral indica a quantidade total
de humidade que est´a sobre a superf´ıcie S.
15/42

16. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios I
1 Calcule S f dS sendo f (x, y, z) = x2 + y2 + z2 + 5
S = (x, y, z) ∈ R3
: x2
+ y2
= z2
, 0 ≤ z ≤ 1 .
R: 6
√
2π
2 Calcule S (x + z) dS onde S ´e a parte do cilindro
y2 + z2 = 9 entre x = 0 e x = 4 contida no 1o octante.
R: 12π + 36
3 Calcule S f dS sendo f (x, y, z) = xy
z
S = (x, y, z) ∈ R3
: x2
+ y2
= z, 4 ≤ x2
+ y2
≤ 16 .
R: 65
3
2 −17
3
2
3
16/42

17. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios II
4 Calcule a ´area da superf´ıcie
S = (x, y, z) ∈ R3
: x2
+ y2
= z, 0 ≤ z ≤ 4
R: π
6 (
√
17
3
− 1)
5 Verifique que a ´area da superf´ıcie de uma esfera unit´aria ´e
4π.
Sug: Use coordenadas esf´ericas.
6 Calcule a ´area da superf´ıcie dada por
x2
+ y2
− z = 0 ∧ z ≤ 9
R: π
2
37
3
2 −1
3
17/42

18. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Orienta¸c˜ao de uma superf´ıcie
Uma superf´ıcie S diz-se orient´avel se podemos definir um
vetor normal unit´ario n a cada ponto de S e de modo que estes
vetores variem continuamente sobre a superf´ıcie S.
Uma superf´ıcie orientada tem dois lados distintos. Assim
quando orientamos uma superf´ıcie escolhemos um dos dois
poss´ıveis vectores normais unit´arios.
18/42

19. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Fita de Mobius
http://www.youtube.com/watch?v=BVsIAa2XNKc&NR=
1&feature=fvwp
19/42

20. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Garrafa de Klein
http://www.youtube.com/watch?v=E8rifKlq5hc
20/42

21. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Defini¸c˜ao (Integral de superf´ıcie de campo vetorial)
Seja S uma superf´ıcie orientada de parametriza¸c˜ao r e
orienta¸c˜ao n, isto ´e, (S, n).
Seja F : Ω −→ R3 um campo vetorial cont´ınuo, tal que
S ⊂ Ω.
Define-se
S
F · dS =
S
F · n dS =
D
F (r(u, v))|
∂r
∂u
×
∂r
∂v
dudv
Nota:
S
F · dS ´e o fluxo que atravessa S com velocidade F, ou
seja, ´e a quantidade de fluido que atravessa a superf´ıcie S por
unidade de tempo.
21/42

22. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Campo vetorial de velocidades (constantes em modulo), v de
um escoamento de agua num tubo infinitesimalmente pequeno.
Quais part´ıculas do fluido contribuir˜ao mais para o fluxo?
v1-Tem a contribui¸c˜ao m´axima poss´ıvel: v1 · n = f1
v3-N˜ao contribui: v1 · n = 0
v2-S´o tem contribui¸c˜ao da componente horizontal.1
1
Pedro Silva,IFMC,ISEL
22/42

23. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcio
Determine se ´e positivo, negativo ou nulo, o fluxo atrav´es das
superf´ıcies abaixo, de
F(x, y, z) = (0, 0, z),
G(x, y, z) = (x, 0, 0),
H(x, y, z) = (0, 1, 0),
J(x, y, z) = (0, 0, z − 2)
23/42

24. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios I
1 Calcule o fluxo de f (x, y, z) = (x, 0, 0) atrav´es das
superf´ıcies
S1 = (x, y, z) ∈ R3
: x = 2, 0 ≤ y ≤ 2, 0 ≤ z ≤ 2
e
S2 = (x, y, z) ∈ R3
: x = 0, 0 ≤ y ≤ 2, 0 ≤ z ≤ 2
segundo a normal com a primeira componente positiva. E
atrav´es da superf´ıcie
S3 = (x, y, z) ∈ R3
: z = 2, 0 ≤ x ≤ 2, 0 ≤ y ≤ 2
segundo a normal com a terceira componente positiva.
Comente o resultado.
24/42

25. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios II
2 Calcule
S
F · n dS sendo
F(x, y, z) = (x, y, 2x + 2y + 2z) e
S = (x, y, z) ∈ R3
: x2
+ y2
= z, z ≤ 4, x ≥ 0, y ≥ 0
segundo uma normal `a sua escolha.
3 Calcule o fluxo de f (x, y, z) = y2z, 0, 0 atrav´es da
superf´ıcie
S = (x, y, z) ∈ R3
: x2
+ y2
= z, z ≤ 4
segundo a normal “exterior”.
25/42

26. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcios III
4 Determine o fluxo de f (x, y, z) = (x, y, z) atrav´es da
superf´ıcie
S = (x, y, z) ∈ R3
: x2
+ y2
= 4 − z, z ≥ 0
orientada por um vector normal unit´ario apontado para
cima.
5 Calcule o fluxo de
f (x, y, z) = y√
x2+y2
, − y√
x2+y2
, 1√
x2+y2
atrav´es da
superf´ıcie
S = (x, y, z) ∈ R3
: z = 1 − x2
− y2
, 0 ≤ z ≤ 1
segundo a normal com a terceira componente positiva.
26/42

27. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Teorema (da Divergˆencia / de Gauss)
Considerem-se:
V um subconjunto limitado de R3 tal que a sua fronteira ´e
uma superf´ıcie S, orientada segundo a normal exterior
(ne).
F um campo vetorial de classe C1 num aberto que
contenha V.
Ent˜ao:
V
divFdx dy dz =
S
F · ne dS.
Nota:
Se F(x, y, z) = (F1, F2, F3) ent˜ao divF = ∂F1
∂x + ∂F2
∂y + ∂F3
∂z .
27/42

28. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Divergˆencia2
Se F(x, y, z) = (F1, F2, F3) ent˜ao divF = ∂F1
∂x + ∂F2
∂y + ∂F3
∂z .
A divergˆencia ´e um escalar que expressa se o campo vectorial
apresenta convergˆencia (contrac¸c˜ao do campo das velocidades)
ou divergˆencia (expans˜ao do campo das velocidades).
2
Pedro Silva,IFMC,ISEL
28/42

29. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Quando:
divF > 0 diz-se que existem fontes de campo, pois o
fluxo que sai da superf´ıcie excede o que entra;
divF < 0 diz-se que existem sumidouros de campo, pois
o fluxo que sai ´e menor que o que entra na superf´ıcie;
divF = 0 diz-se que o campo vectorial ´e solen´oidal.
29/42

30. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcio
Determine se ´e positiva, negativa ou nula a divergˆencia do
campo vectorial representado abaixo (representado no xOy pois
n˜ao tem componente em z e ´e independente de z) nos pontos
indicados.
negativa; negativa.
30/42

31. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
O Teorema da divergˆencia mostra que a divergˆencia pode ser
interpretada como o balan¸co de fluxo que entra e sai por
unidade de volume, atrav´es da superf´ıcie que o encerra.
https:
//www.khanacademy.org/math/multivariable-calculus/
divergence_theorem_topic/divergence_theorem/v/
3-d-divergence-theorem-intuition
31/42

32. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
1 Verifique o Teorema da Divergˆencia sendo
A = (x, y, z) ∈ R3
: x2
+ y2
≤ z, z ≤ 1
e F(x, y, z) = (0, 0, z).
2 Calcule, usando o T. Div., o integral A F · n dS onde
n ´e a normal com a terceira componente negativa,
F(x, y, z) = (x, z, y) e
A = (x, y, z) ∈ R3
: x2
+ y2
= z2
, 0 ≤ z ≤ 1 .
3 Usando o T.Div. calcule o fluxo de G(x, y, z) = (−z, y, y)
atrav´es de
A = (x, y, z) ∈ R3
: z = 9 − x2
− y2
, z ≥ 0, x ≤ 0
no sentido da normal com a terceira componente negativa.
32/42

33. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
4 Usando o T. Div. calcule o volume da regi˜ao
A = (x, y, z) ∈ R3
: y2
+ z2
≤ 9, z ≥ 0, |x| ≤ 5 .
5 Calcule o fluxo de G(x, y, z) = (2x, −y, 1 − z) atrav´es de
A = (x, y, z) ∈ R3
: z = 1 − x2
− y2
, y ≥ 0, z ≥ 0
no sentido da normal com a terceira componente positiva.
6 Considere as regi˜oes
A = (x, y, z) ∈ R3
: z = 2 − x2
− y2
, x ≥ 0, z ≥ 1
e
B = (x, y, z) ∈ R3
: z2
= x2
+ y2
, 0 ≤ z ≤ 1 .
Seja H(x, y, z) = (0, 0, z). Calcule o volume do interior de
S1 ∪ S2 usando o T. Div.
33/42

34. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Rotacional3
Sendo F(x, y, z) = (F1, F2, F3),
RotF =
e1 e2 e3
∂
∂x
∂
∂y
∂
∂z
F1 F2 F3
=
=
∂F3
∂y
−
∂F2
∂z
e1 +
∂F1
∂z
−
∂F3
∂x
e2 +
∂F2
∂x
−
∂F1
∂y
e3
=
∂F3
∂y
−
∂F2
∂z
,
∂F1
∂z
−
∂F3
∂x
,
∂F2
∂x
−
∂F1
∂y
3
Pedro Silva,IFMC,ISEL
34/42

35. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
As figuras seguintes apresentam um aparelho para medir a
circula¸c˜ao (moinho de p´as) e um campo vetorial.
Repare que se a vara do moinho estiver ”deitada”sobre o
campo vetorial o moinho n˜ao roda.
Se a vara estiver vertical o moinho roda.
O vetor RotF aponta no sentido da vara, segindo a dire¸c˜ao da
”regra da m˜ao direita”. ´E nulo se o campo vetorial n˜ao
produzir rota¸c˜ao.
35/42

36. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Regra da m˜ao direita
36/42

37. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Considere-se o campo de velocidades simplificado de um
escoamento numa conduta (escoamento no plano xy):
1) o ´unico termo do rotacional que ´e diferente de zero ´e
∂F1
∂y > 0, o que resulta num rotacional diferente de zero e
negativo,
RotF = −
∂F1
∂y
e3
2) tamb´em o ´unico termo do rotacional que ´e diferente de zero
´e ∂F1
∂y < 0 que resulta num rotacional diferente de zero e
positivo,
RotF =
∂F1
∂y
e3
3) uma vez que a velocidade n˜ao apresenta efeito de corte (´e
constante com y), n˜ao existe rota¸c˜ao; de facto, todos os
termos do rotacional s˜ao zero. 37/42

38. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Exerc´ıcio
Considere os campos vectoriais
(a)F(x, y, z) = (x, y, 0)
(b) F(x, y, z) = (y, −x, 0)
(c) F(x, y, z) = (−(y + 1), 0, 0)
A figura abaixo mostra a sua representa¸c˜ao (para qualquer z,
pois s˜ao independentes de z)
Calcule e interprete RotF(0, 0, 0).
38/42

39. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Teorema (de Stokes)
Considerem-se:
S uma superf´ıcie orient´avel dada por:
S ≡ r(u, v), (u, v) ∈ D com r de classe C2 num aberto
que contenha D ∪ ∂D;
∂S uma linha seccionalmente regular que ´e bordo de S
(transformado por r da fronteira de D: r(frD)).
n um vector unit´ario normal S com sentido em
concordˆancia com o sentido do ∂S segundo a “Regra da
m˜ao direita”.
F um campo vetorial de classe C1 num aberto que
contenha S ∪ ∂S.
Ent˜ao:
S
RotF · dS =
∂S
F · dr.
39/42

40. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Teorema de Stokes – Intui¸c˜ao
https://www.khanacademy.org/math/
multivariable-calculus/surface-integrals/stokes_
theorem/v/stokes--theorem-intuition
40/42

41. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
1 Verifique o Teorema de Stokes sendo
A = (x, y, z) ∈ R3
: x2
+ y2
= z, z ≤ 4
e F(x, y, z) = (1, 0, 1 − x).
(Use a parametriza¸c˜ao em coordenadas cartesianas e
polares.) R:4π
2 Usando o T. Stokes calcule S RotF · dS sendo
F(x, y, z) = (x + 1, 0, 0) e S a superf´ıcie
S = (x, y, z) ∈ R3
: x2
+ y2
= z2
, 0 ≤ z ≤ 9
que tem orienta¸c˜ao dada pela normal que tem a
componente em z negativa.
R:0
41/42

42. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
3 Usando o T. Stokes, calcule o trabalho realizado no
deslocamento de um ponto material ao longo do bordo de
A, percorrido uma s´o vez, no sentido direto por ac¸c˜ao de
G(x, y, z) = (0, x, 0), sendo
A = (x, y, z) ∈ R3
: x2
+ y2
= 9, x + y + z = 4
4 Sejam
A = (x, y, z) ∈ R3
: x2
+ y2
+ z2
= 1, z ≥ 0
e H(x, y, z) = (−y, x, 1). Usando o T. Stokes, calcule o
fluxo de RotF, atrav´es de A no sentido da normal com a
terceira componente positiva.
R:2π
42/42

43. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
5 Calcule o fluxo de RotF sendo F(x, y, z) = (z, x, y)
atrav´es de
A = (x, y, z) ∈ R3
: x2
+ y2
= 1, −1 ≤ z ≤ 2
segundo a normal que tem a componente em z negativa.
R:0
6 Usando o T. Stokes, calcule o trabalho realizado pelo
campo F(x, y, z) = (0, 0, x) ao longo da parte da linha
A = (x, y, z) ∈ R3
: x2
+ y2
= 1, z = 1
com origem em (1,0,1), extremidade em (0,-1,1) e que
passa por (0,1,1).
43/42

44. AM2
Superf´ıcie
Vetor normal
e plano
tangente
Integral de
superf´ıcie de
campo escalar
Integral de
superf´ıcie de
campo vetorial
Teorema da
divergˆencia
Teorema de
Stokes
Autora:
Sandra Gaspar Martins
Com base no trabalho de:
Nuno David Lopes
e
Cristina Janu´ario
44/42