Sandra Gaspar Martins, profile picture
Carregado porSandra Gaspar Martins
PDF, PPTX1,238 visualizações

02 Campos Escalares e Vectoriais

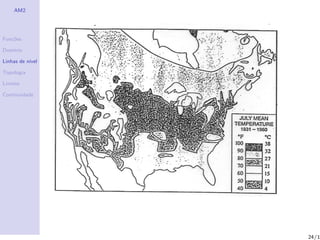
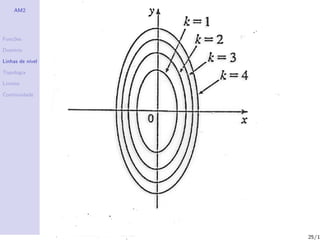
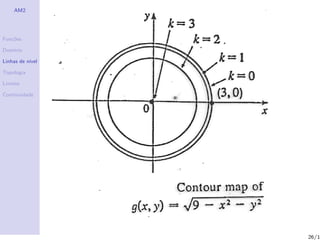
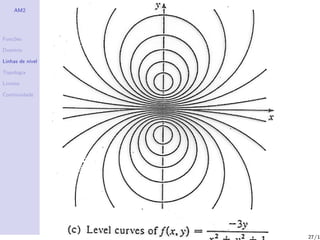
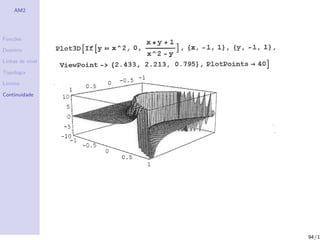
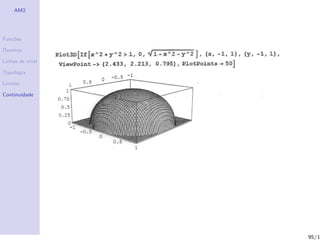
O documento aborda o estudo de funções de várias variáveis, focando em suas propriedades de continuidade, domínios e linhas de nível. Também são apresentados exemplos de campos escalares e vetoriais, além de definições importantes dentro da topologia e análise matemática. Exercícios práticos são incluídos para auxiliar na compreensão dos conceitos discutidos.

Incorporar apresentação

Transferir como PDF, PPTX
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Campos escalares e vectoriais - Parte 1 Topologia Limites An´lise Matem´tica 2 a a Continuidade 2o Semestre 2011/12 Vers˜o de 16 de Maio de 2012 a 1/1
AM2 Fun¸oes c˜ Fun¸˜es co Neste cap´ ıtulo trabalhamos com fun¸˜es co Dom´ ınio Linhas de n´ ıvel f : Rn −→ Rm (n, m ∈ N, n˜o simultˆneamente iguais a 1) a a Topologia Limites Se m = n = 1 estas fun¸˜es designam-se por fun¸˜es reais de co co Continuidade vari´vel real e foram estudadas em AM1. a f : R −→ R Se m = 1 estas fun¸˜es designam-se por campos escalares ou co fun¸˜es escalares. co f : Rn −→ R (n > 1) Se m > 1 estas fun¸˜es designam-se por campos vectoriais ou co fun¸˜es vectoriais. co f : Rn −→ Rm (n ≥ 1) 2/1
AM2 Exemplos: Fun¸˜es co Dom´ ınio 1 f : D ⊂ R3 −→ R tal que f (x, y , z) = x + y + z Linhas de n´ ıvel Topologia 2 f : D ⊂ R2 −→ R4 tal que Limites x Continuidade f (x, y ) = x + y , x − y , xy , y 3 f : D ⊂ R2 −→ R tal que f (latitude, longitude) = (altitude) 4 f : D ⊂ R2 −→ R3 tal que f (latitude, longitude) = (altitude, humidade, temperatura) 5 f : D ⊂ R2 −→ R2 tal que f (latitude, longitude) = vector que indica a direc¸˜o e intensidade do vento ca 6 f : D ⊂ R3 −→ R3 tal que f (x, y , z) = vector que indica a direc¸˜o de escoamento de um flu´ em ca ıdo movimento 3/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 4/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 5/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 6/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 7/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 8/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 9/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 10/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 11/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 12/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 13/1
AM2 Dado o campo vectorial Fun¸˜es co Dom´ ınio f : R2 −→ R4 Linhas de n´ ıvel Topologia x Limites f (x, y ) = xy , x 2 − y , x − 3y , √ Continuidade y ´ composto por 4 fun¸˜es componentes ou fun¸˜es e co co coordenadas que s˜o: a f1 (x, y ) = xy f2 (x, y ) = x 2 − y f3 (x, y ) = x − 3y x f4 (x, y ) = √ y Nota: estas fun¸˜es s˜o campos escalares. co a 14/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Fa¸a um esbo¸o do gr´fico das seguintes fun¸˜es: c c a co Linhas de n´ ıvel Topologia 1 f (x, y ) = 5 Limites 2 f (x, y ) = x Continuidade 3 f (x, y ) = x + y 4 f (x, y ) = y 2 5 f (x, y ) = 2 + cos(x) 6 f (x, y ) = x 2 + y 2 7 f (x, y ) = − x 2 + y 2 + 3 8 f (x, y ) = − x 2 + y 2 + 3 9 f (x, y ) = 9 − x2 − y2 √ 10 f (x, y ) = − 25 − x 2 15/1
AM2 Dom´ ınio Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o (Dom´ de uma fun¸˜o) ca ınio ca Limites Dada uma fun¸˜o f : Rn −→ Rm (n, m ≥ 1) define-se o ca Continuidade dom´ınio de f por Df = {x ∈ Rn : ∃1 y ∈ IR m , f (x) = y } Exemplo: x f : D ⊂ R2 −→ R4 tal que f (x, y ) = x + y , x − y , xy , y tem como dom´ D = {(x, y ) ∈ R2 : y = 0} ınio 16/1
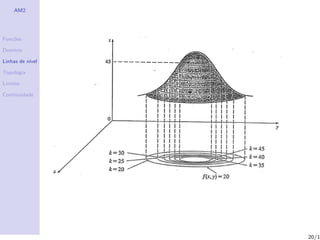
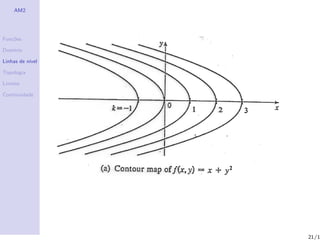
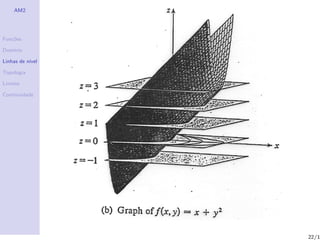
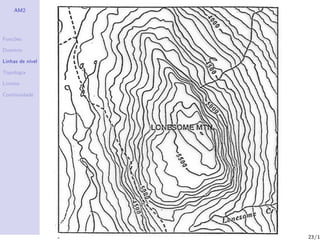
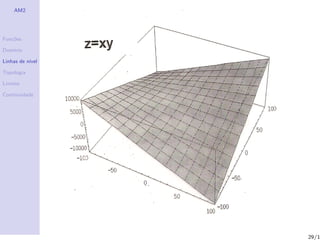
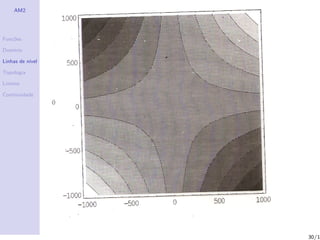
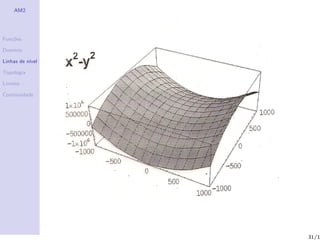
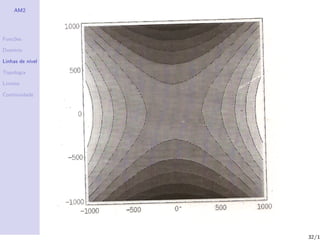
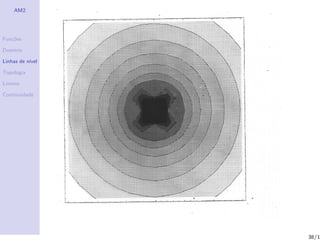
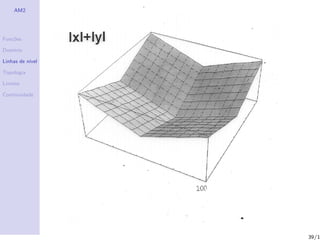
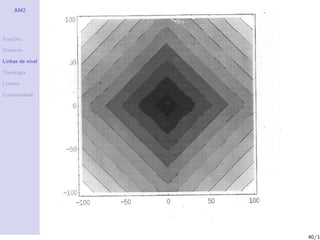
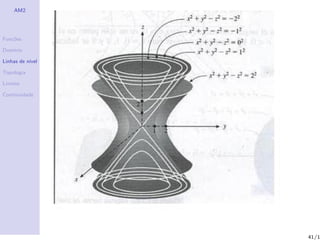
AM2 1 ⇒ a ∈ R {0} Fun¸˜es co a √ Dom´ ınio a ⇒ a ∈ R+ 0 Linhas de n´ ıvel ln(a) ⇒ a ∈ R+ Topologia Limites |a| ⇒ a ∈ R Continuidade an ⇒ a ∈ R (n ∈ N) cos(a) ⇒ a ∈ R sin(a) ⇒ a ∈ R π tan(a) ⇒ a ∈ R + kπ, k ∈Z 2 arccos(a) ⇒ a ∈ [−1, 1] arcsin(a) ⇒ a ∈ [−1, 1] arctan(a) ⇒ a ∈ R ... 17/1
AM2 Fun¸˜es co Determine o dom´ das seguintes fun¸˜es e represente-o ınio co Dom´ ınio geometricamente: Linhas de n´ ıvel 1 f (x, y ) = (ln(x), ln(y ), x − y ) Topologia x Limites 2 f (x, y ) = y Continuidade 3 f (x, y ) = √ 1 2 2 4−x −y √ 4 f (x, y ) = ( −x 2 + 1, 4 − y 2) −3 5 f (x, y , z) = ( √ , ze x , y ) x 2 +y 2 +z 2 −9 √ 6 f (x, y ) = arcsin( x ) + xy 2 7 f (x, y ) = ln( x−y ) 2x 8 f (x, y ) = y − 2x 2 18/1
AM2 Linhas e Superf´ ıcies de N´ ıvel Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Seja f : R2 −→ R chama-se curva ou linha de n´ k ao ıvel Limites Continuidade conjunto: Nk = {(x, y ) ∈ R2 : k = f (x, y ), (x, y ) ∈ Df } (k ∈ Df ) Se f : R3 −→ R chama-se superf´ de n´ k ao ıcie ıvel conjunto: Nk = {(x, y , z) ∈ R3 : k = f (x, y , z), (x, y , z) ∈ Df } (k ∈ Df ) http://www.flashandmath.com/mathlets/multicalc/contours/index.html 19/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 20/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 21/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 22/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 23/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 24/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 25/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 26/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 27/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Calcule algumas linhas de n´ das fun¸˜es que se seguem at´ ıvel co e Topologia conseguir fazer um esbo¸o do gr´fico da fun¸˜o: c a ca Limites 1 f (x, y ) = xy Continuidade 2 f (x, y ) = x 2 − y 2 3 f (x, y ) = y − cos(x) 1 4 f (x, y ) = e x 2 +y 2 5 f (x, y ) = ln(x 2 + y 2 ) 6 f (x, y ) = |x| + |y | 7 f (x, y , z) = x2 + y2 − z2 (ver figuras) 28/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 29/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 30/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 31/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 32/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 33/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 34/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 35/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 36/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 37/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 38/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 39/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 40/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 41/1
AM2 Distˆncia a Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o (Distˆncia) ca a Limites Continuidade Dados dois pontos de Rn , P = (x1 , ..., xn ) e P = (x1 , ...xn ) a distˆncia euclideana entre eles ´ dada por a e d(P, P ) = (x1 − x1 )2 + (x2 − x2 )2 + ... + (xn − xn )2 −→ − Nota: d(P, P ) = ||PP || ´ a norma ou comprimento do vector e −→ − PP . 42/1
AM2 Bola aberta ou Vizinhan¸a c Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Defini¸˜o (Bola aberta ou Vizinhan¸a) ca c Continuidade Diz-se vizinhan¸a ε de um ponto a ∈ Rn (Bola aberta de c centro em a e raio ε) ao conjunto Bε (a) = {x ∈ Rn : d(x, a) < ε} ou Bε (a) = {x ∈ Rn : ||x − a|| < ε}. 43/1
AM2 Fun¸˜es co Dom´ ınio Calcule: Linhas de n´ ıvel B5 (3) = Topologia Limites Continuidade B2 (2, −3) = B3 (1, 2, 3) = 44/1
AM2 Defini¸˜o ca Seja a ∈ Rn e X ⊂ Rn . Fun¸˜es co Dom´ ınio a ´ interior a X se e Linhas de n´ ıvel Topologia ∃ε : Bε (a) ⊂ X ; Limites Continuidade se existe uma Bola de centro em a toda contida em X . a ´ exterior a X se e ∃ε : Bε (a) ⊂ Rn X ; se existe uma Bola de centro a que n˜o tem pontos de X . a a ´ fronteiro a X se ∀ε > 0 e Bε (a) ∩ X = ∅ e Bε (a) ∩ (Rn X ) = ∅, se qualquer Bola de centro em a tem pontos de X e de Rn X . 45/1
AM2 Defini¸˜o ca Fun¸˜es co Seja a ∈ Rn e X ⊂ Rn . Dom´ ınio Linhas de n´ ıvel a ´ ponto de acumula¸˜o de X se e ca Topologia Limites ∀ε > 0, Bε (a) ∩ (X {a}) = ∅; Continuidade se qualquer vizinhan¸a de a tem infinitos pontos de X c distintos de a. a ´ ponto isolado de X se e ∃ε > 0, : Bε (a) ∩ X = {a}; se existe uma Bola de centro em a que o unico ponto que ´ tem de X ´ o pr´prio a. e o a ´ aderente a X se a ∈ X ou a ∈ fr (X ) e 46/1
AM2 Defini¸˜o ca Fun¸˜es co Interior de X : int(X ) ´ o conjunto dos pontos interiores e Dom´ ınio Linhas de n´ ıvel aX Topologia Exterior de X :ext(X ) ´ o conjunto dos pontos exteriores e Limites aX Continuidade Fronteira de X : fr (X ) ´ o conjunto dos pontos fronteiros e de X Derivado de X : X ´ o conjunto dos pontos de e acumula¸˜o de X ca ¯ e Aderˆncia de X : X ´ o conjunto dos pontos aderentes a e X Teorema int(X ) ∪ ext(X ) ∪ fr (X ) = Rn e s˜o disjuntos 2 a 2 a 47/1
AM2 Fun¸˜es co Defini¸˜o ca Dom´ ınio Um conjunto X de Rn ´ e Linhas de n´ ıvel Topologia aberto se X = int(X ) (⇔ X ∩ fr (x) = ∅) Limites ¯ fechado se X = X (⇔ fr (X ) ⊂ X ) Continuidade limitado se existir uma bola que o contenha. compacto se for limitado e fechado. Nota: Existem conjuntos que n˜o s˜o abertos nem fechados a a ∅ e Rn s˜o abertos e fechados. a 48/1
AM2 Seja X o conjunto de R2 colorido a vermelho: Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade Complete: { } ∈ int(X ) { } ∈ ext(X ) { } ∈ fr (X ) { }∈X { ¯ }∈X { } ∈ Pontos Isolados de X 49/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel 1 Classifique topologicamente os conjuntos: Topologia 1 A = (x, y ) ∈ R2 : −x 2 + 1 < y < −2x 2 + 2 Limites 2 B = (x, y ) ∈ R2 : |x| ≤ 1 ∧ |y | ≤ e x Continuidade 3 C = (x, y ) ∈ R2 : (x 2 + y 2 − 1)(4 − x 2 − y 2 ) > 0 2 Calcule o dom´ ınio, Df , das seguintes fun¸˜es. Represente co geometricamente e classifique topologicamente Df . 1 f (x, y ) = x(1 − |y |) x 2 +y 2 (x, y ) = (0, 0) 2 f (x, y ) = x−y 1 (x, y ) = (0, 0) x 3 f (x, y ) = ln( y ) + arcsin(x 2 + y 2 ) 4 f (x, y ) = ln(y − x) 9 − x 2 − (y + 1)2 50/1
AM2 Limite Fun¸˜es co Defini¸˜o (Limite de campo escalar definido em R2 ) ca Dom´ ınio Linhas de n´ ıvel Seja f : Df ⊆ R2 −→ R e (x0 , y0 ) um ponto de acumula¸˜o do ca Topologia dom´ Df . ınio Limites O limite de f (x, y ) quando (x, y ) tende para (x0 , y0 ) ´ l, e e Continuidade escreve-se lim f (x, y ) = l (x,y )→(x0 ,y0 ) se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀(x, y ) ∈ Df {(x0 , y0 )}, (x, y ) ∈ Bε (x0 , y0 ) =⇒ f (x, y ) ∈ Bδ (l) ou seja, (x − x0 )2 + (y − y0 )2 < ε =⇒ |f (x, y ) − l| < δ) 51/1
AM2 Geometricamente Fun¸˜es co Este limite implica que, Dom´ ınio para qualquer ponto (x, y ) = (x0 , y0 ) do dom´ de f , ınio Linhas de n´ ıvel no disco de raio ε, Topologia o valor de f (x, y ) esteja entre os planos de equa¸˜o z = l − δ e ca Limites z = l + δ, Continuidade ou seja, todos contidos no cilindro de raio ε e altura 2δ. 52/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 53/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 54/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 55/1
AM2 Exemplo: Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Vejamos se Topologia lim 5+4 x2 + y2 = 5 (x,y )→(0,0) Limites Continuidade ou seja, vejamos se ∀δ > 0, ∃ε(δ) > 0 : ∀(x, y ) ∈ Df {(0, 0)}, (x, y ) ∈ Bε (0, 0) =⇒ f (x, y ) ∈ Bδ (5) ou seja, (x − 0)2 + (y − 0)2 < ε =⇒ |f (x, y ) − 5| < δ) 1 1 Determine ε sendo δ = 10, δ = 10 , δ= 100 , δ qualquer... 56/1
AM2 Revis˜es: o |ab| = |a| |b| a |a| Fun¸˜es co = Dom´ ınio b |b| Linhas de n´ ıvel |a + b| ≤ |a| + |b| Topologia Limites Continuidade ab = |a|b √ |a| = a2 |a| ≤ a2 + b 2 a2 0≤ ≤1 a2 + b2 | sin(a)| ≤ 1 π | arctan(a)| ≤ 2 57/1
AM2 Exerc´ ıcios: I Fun¸˜es co Dom´ ınio Mostre, por defini¸˜o de limite, que: ca Linhas de n´ ıvel 1 lim f (x, y ) = 0 onde f (x, y ) = 3 x 2 + y 2 cos(xy ) (x,y )→(0,0) Topologia Limites Continuidade 2 lim f (x, y ) = 0 onde (x,y )→(0,0) f (x, y ) = 2 sin(x + y ) x 2 + y 2 3 lim f (x, y ) = 7 onde f (x, y ) = 2x + y (x,y )→(2,3) 4 lim x =2 (x,y )→(2,1) 5 lim 4xy = 0 (x,y )→(0,0) 58/1
AM2 Exerc´ ıcios: II Fun¸˜es co x 2y 2 6 lim = 0 (ver fig.) Dom´ ınio (x,y )→(0,0) x2 + y2 Linhas de n´ ıvel Topologia 4x 3 Limites 7 lim =0 Continuidade (x,y )→(0,0) x 2 + y2 1 8 lim = 0 (se poss´ - ver fig.) ıvel (x,y )→(0,0) x 2 + y2 x 4 + 2y 3 9 lim =0 (x,y )→(0,0) x 2 + y 2 y 10 lim xy sin( ) = 0 (x,y )→(0,0) x 59/1
AM2 Exerc´ ıcios: III Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 11 lim (x 2 + y 2 ) arctan(xy ) = 0 (x,y )→(0,0) 60/1
AM2 Limite Fun¸˜es co Dom´ ınio Defini¸˜o (Limite de campo escalar definido em Rn ) ca Linhas de n´ ıvel Seja f : Df ⊆ Rn −→ R e a um ponto de acumula¸˜o do ca Topologia dom´ Df . ınio Limites O limite de f (x) quando x tende para a ´ l, e escreve-se e Continuidade lim f (x) = l x→a se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀x ∈ Df {a}, x ∈ Bε (a) =⇒ f (x) ∈ Bδ (l) ou seja, (x1 − a1 )2 + ...(xn − an )2 < ε =⇒ |f (x) − l| < δ) 61/1
AM2 Proposi¸˜o (Propriedades dos limites) ca Fun¸˜es co Sejam f : Df ⊆ Rn −→ R e g : Dg ⊆ Rn −→ R duas fun¸˜es co Dom´ ınio escalares e a um ponto de acumula¸˜o de Df ∩ Dg . ca Linhas de n´ ıvel Se limx→a f (x) = l1 e limx→a g (x) = l2 ent˜o a Topologia Limites O limite ´ unico. e´ Continuidade lim (f (x) + g (x)) = l1 + l2 x→a lim (f (x).g (x)) = l1 .l2 x→a f (x) l1 lim = x→a g (x) l2 lim (cf (x)) = c.l1 x→a 62/1
AM2 Limite relativo Fun¸˜es co Dom´ ınio Defini¸˜o (Limite relativo a um conjunto) ca Linhas de n´ ıvel Topologia Seja S um subconjunto de Df , f : Df ⊆ Rn −→ R e a um Limites ponto de acumula¸˜o do dom´ Df . O limite de f (x) ca ınio Continuidade relativo a S quando x tende para a ´ l, e escreve-se e lim f (x) = l x→a x∈S se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀x ∈ S {a}, x ∈ Bε (a) =⇒ f (x) ∈ Bδ (l) No caso em que S = (x, y ) ∈ R2 : y = mx + b a estes limites chamam-se os limites direccionais. 63/1
AM2 Fun¸˜es co Dom´ ınio Proposi¸˜o ca Linhas de n´ ıvel Se o limite existir ent˜o o limite relativo a qualquer conjunto a Topologia existe e tem o mesmo valor. Limites Continuidade Exerc´ ıcio: Que pode concluir se encontrar dois limites relativos diferentes? iguais? 64/1
AM2 Exerc´ ıcios Fun¸˜es co Utilize limites relativos para estudar os limites: Dom´ ınio x2 1 lim (ver fig.) (x,y )→(0,0) x 2 + y 2 Linhas de n´ ıvel Topologia Limites xy Continuidade 2 lim (ver fig.) (x,y )→(0,0) x 2 + y2 x 3 lim (ver fig.) (x,y )→(0,0) x 2 + y2 x −y 4 lim (x,y )→(0,0) x + y 4xy 5 lim (x,y )→(0,0) x 2+ y2 xy 2 6 lim(x,y )→(0,0) (x+y 2 )2 65/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 66/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 67/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 68/1
AM2 Limites e propriedades Fun¸˜es co Dom´ ınio Defini¸˜o (Limites iterados ou sucessivos) ca Linhas de n´ ıvel Topologia Seja f : Df ⊂ R2 −→ R e (a, b) um ponto de acumula¸˜o do ca Limites dom´ Df , ent˜o os limites ınio a Continuidade lim lim f (x, y ) , lim lim f (x, y ) x→a y →b y →b x→a dizem-se limites iterados ou sucessivos. Nota: o caso geral, de uma fun¸˜o definida em Rn , ´ ca e limx1 →a1 (· · · (limxn →an f (x1 , · · · , xn ))). Proposi¸˜o ca Se dois limites iterados forem diferentes (existirem e forem finitos) ent˜o n˜o existe limite. a a 69/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Utilize limites iterados para estudar os limites: Continuidade x − 2y 1 lim (x,y )→(0,0) x + y 4xy 2 lim (x,y )→(0,0) (x 2 + y 2 )5 70/1
AM2 Exerc´ ıcios Globais de Limites I Fun¸˜es co Dom´ ınio Estude a existˆncia dos seguintes limites. e Linhas de n´ ıvel x 4 + 2y 2 Topologia 1 lim (x,y )→(0,0) x 2 + y 2 Limites Continuidade y2 2 lim (x,y )→(0,0) x 2 + y2 x 2y 3 lim (x,y )→(0,0) (x 2 + y 2 )2 y −2 4 lim (x,y )→(−3,2) x + 3 72/1
AM2 Exerc´ ıcios Globais de Limites II Fun¸˜es co xy + 3 5 lim Dom´ ınio (x,y )→(0,0) 1 − 2x 2 Linhas de n´ ıvel Topologia xy 2 Limites 6 lim (x,y )→(0,0) x 2 + y 4 Continuidade 1 7 lim x sin (x,y )→(0,0) y xy 8 lim (x,y )→(0,0) x 2 + 3y 2 x 2y 9 lim (x,y )→(0,0) (x 2 + y )2 73/1
AM2 Exerc´ ıcios Globais de Limites III Fun¸˜es co x 4y Dom´ ınio 10 lim (x,y )→(0,0) y 3 − x 6 Linhas de n´ ıvel Topologia Limites x 2y 11 lim Continuidade (x,y )→(0,0) (y + x 2 )2 x +y −2 12 lim (x,y )→(1,1) x −y 13 limite de f nos pontos (0, 0); (1, 1); (1, 0); (0, 1), sendo   1 − 2y + x se x + y < 1 f (x, y ) = 1 se x + y = 1 2 − x + y se x + 1 > 1.  74/1
AM2 Exerc´ ıcios Globais de Limites IV Fun¸˜es co Dom´ ınio 14 limite de f nos pontos (1, 1); (−1, 0); (0, 2), sendo Linhas de n´ ıvel  Topologia  x +y se x > 0 Limites f (x, y ) = 2 se x = 0 x − y + 2 se x < 0.  Continuidade 15 indique para que pontos da recta y = −x existe limite de f , sendo   1 − 2y + x se x + y < 0 f (x, y ) = 4 se x + y = 0 6−x +y se x + 1 > 0.  75/1
AM2 Exerc´ ıcios Globais de Limites V Fun¸˜es co Dom´ ınio 16 limite de f nos pontos (1, 2); (2, 1); (2, 2), sendo Linhas de n´ ıvel Topologia 2x − y se y < x f (x, y ) = Limites x2 se y ≥ x. Continuidade 17 lim g (x, y ) e lim g (x, y ) onde (x,y )→(0,0) (x,y )→(0,2)  4−x 2 −y 2  e se x 2 + y 4 ≥ 4 g (x, y ) = e se (x, y ) = (0, 0) 1 se x 2 + y 2 < 4  x 2 +y 2 76/1
AM2 Exerc´ ıcios Globais de Limites VI Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites 18 lim f (x, y ) onde Continuidade (x,y )→(0,−4) x2 x 2 +(y +4)2 se (x, y ) = (0, −4) f (x, y ) = 1 se (x, y ) = (0, −4) 77/1
AM2 Limite Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o (Limite de fun¸˜es vectoriais) ca co Topologia Seja Limites Continuidade f : Df ⊆ Rn −→ Rm x −→ y = f (x) = (f1 (x), ..., fm (x)) e a um ponto de acumula¸˜o do dom´ Df =D ca ınio . f1 ∩Df2 ∩...∩Dfm O limite de f (x) quando x tende para a ´ um vector de m e coordenadas onde cada uma corresponde ao limite da fun¸˜o ca coordenada respectiva. Assim lim f (x) = lim f1 (x), ... lim fm (x) x→a x→a x→a 78/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade Calcule: 1 lim f (x, y ) onde f (x, y ) = (x 2 , xy 2 ) (x,y )→(1,2) 3xy 2 lim f (x, y ) onde f (x, y ) = ln(4 − x 2 − y 2 ), x 2 +y 2 (x,y )→(0,0) 79/1
AM2 Fun¸˜o composta (campos ca Fun¸˜es co escalares) Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Sejam g : Dg ⊆ Rn −→ R e f : Df ⊆ R −→ R duas fun¸˜es co Limites escalares. Define-se a fun¸˜o composta de f com g como ca Continuidade f : D ⊆ Rn −→ R x −→ (f ◦ g )(x) = f (g (x)) sendo D = {x ∈ Rn : x ∈ Dg ∧ g (x) ∈ Df } 80/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites √ Continuidade 1 Seja f (t) = t e g (x, y ) = x 2 + y 2 + 2. Calcule (f ◦ g )(1, 3), (f ◦ g )(1, 1) e (f ◦ g )(x, y ). 2 Seja f (t) = t 3 e g (x, y ) = x − 4y . Calcule (f ◦ g )(1, 3), (f ◦ g )(1, 1) e (f ◦ g )(x, y ). 81/1
AM2 Fun¸˜o composta (campos ca Fun¸˜es co vectoriais) Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Sejam g : Dg ⊆ Rn −→ Rp e f : Df ⊆ Rp −→ Rm duas Limites fun¸˜es vectoriais. Define-se a fun¸˜o composta de f com g co ca Continuidade como f ◦ g : D ⊆ Rn −→ Rm x −→ (f ◦ g )(x) = f (g (x)) sendo D = x ∈ Rn : x ∈ Dg ∧ g (x) ∈ Df 82/1
AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites 1 Seja f (u, v ) = (e u , e v ) e g (x, y , z) = (x 2 + 2y 2 + z 2 , xyz). Continuidade Calcule, se existir, (f ◦ g )(1, 2, 3), (f ◦ g )(1, 1, 1), (f ◦ g )(x, y , z) e (g ◦ f )(x, y ). 2 Seja f (u, v ) = (u + v , u − v , uv ) e g (x, y , z) = (xy , yz). Calcule, se exisitir, (f ◦ g )(1, 2, 3), (f ◦ g )(1, 1, 1), (f ◦ g )(x, y , z) e (g ◦ f )(x, y ). 83/1
AM2 Continuidade Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o ca Limites Seja f : Df ⊂ Rn −→ R, e a um ponto de Df . Diz-se que f ´ e Continuidade cont´ınua em a se e s´ o ∃ lim f (x) e lim f (x) = f (a) x→a x→a Defini¸˜o ca f diz-se cont´ ınua num dado conjunto S se f ´ cont´ e ınua em todos os pontos de S. Nota: Se S = Df diz-se simplesmente que f ´ cont´ e ınua. 84/1
AM2 Propriedades das fun¸˜es co Fun¸˜es co cont´ ınuas Dom´ ınio Linhas de n´ ıvel Proposi¸˜o ca Topologia Limites Sejam f e g duas fun¸˜es escalares com dom´ contido em co ınio Continuidade Rn e cont´ ınuas em a. Ent˜o, a f f + g, f − g, f .g e (g (a) = 0) g s˜o cont´ a ınuas em a. Proposi¸˜o ca Sejam g : Dg ⊆ Rn −→ R cont´ ınua em a e f : Df ⊆ R −→ R cont´ ınua em g (a). Ent˜o a f ◦ g ´ cont´ e ınua em a. 85/1
AM2 Exerc´ ıcios I Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Estude quanto ` continuidade:1 (ver figuras) a Topologia 1 Limites x2 + sin(x + y ) − e cos(y ) f (x, y ) = Continuidade x −3 2  2xy se (x, y ) = (0, 0)  f (x, y ) = x2+ y2  0 se (x, y ) = (0, 0) 3 xy 2  se (x, y ) = (0, 0)  f (x, y ) = x2 + y2 0 se (x, y ) = (0, 0)  86/1
AM2 Exerc´ ıcios II Fun¸˜es co 4  xy x 2 − y 2  Dom´ ınio Linhas de n´ ıvel se (x, y ) = (0, 0) f (x, y ) = x2 + y2 Topologia 0 se (x, y ) = (0, 0)  Limites Continuidade 5   2x + 3y se x = y f (x, y ) = x −y  5 se x = y 6   xy + 1 se y = x 2 f (x, y ) = x2 − y  0 se y = x 2 7 1 − x 2 − y 2 se x 2 + y 2 ≤ 1 f (x, y ) = 0 se x 2 + y 2 > 1 87/1
AM2 Exerc´ ıcios III Fun¸˜es co 8 Dom´ ınio x +y se x = y Linhas de n´ ıvel f (x, y ) = 0 se x = y Topologia Limites 9 xy Continuidade se x 2 = y 2 f (x, y ) = x2 − y2 0 se x 2 = y 2 10 (x − 1)y 2  se (x, y ) = (1, 0)  f (x, y ) = (x − 1)2 + y 2 10 se (x, y ) = (1, 0)  11 x + y se y ≤ x 2 f (x, y ) = 3x − 1 se y > x 2 88/1
AM2 Exerc´ ıcios IV Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia 12 Limites e y − 2x se y ≤ 2x Continuidade f (x, y ) = ln(y − 2x) se y > 2x 13   1 − 2y + x se y + x < 0 f (x, y ) = 4 se y + x = 0 6−x +y se y + x > 0  1 Pode confirmar usando http://math.hws.edu/xFunctions/ 89/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 90/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 91/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 92/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 93/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 94/1
AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 95/1
AM2 Prolongamento cont´ ınuo Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Uma fun¸˜o f : Df ⊂ Rn −→ R diz-se prolong´vel por ca a Topologia continuidade ao ponto a ( a ∈ Df ), Limites se e s´ se o Continuidade a ∈ Df e existe lim f (x) . (x)→a O Prolongamento (cont´ ınuo) de f a a ´ e f (x) se x ∈ Df f (x) = lim f (x) se x = a x→a Nota: esta fun¸˜o ´ cont´ ca e ınua. 96/1
AM2 Exerc´ ıcios I Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Determine, se existirem, prolongamentos cont´ ınuos de: Limites 1 − 1 f (x, y ) = e x 2 +y 2 Continuidade 1 2 f (x, y ) = x 2 cos x 2 +y 2 x 2y 3 f (x, y ) = x 4 +y −sin(x) ao ponto (0, 0) x2 4 f (x, y ) = x 3 +y −tan(x) ao ponto (0, 0) x 3 cos(y )+y 3 cos(x) 5 f (x, y ) = x 2 +y 2 ao ponto (0, 0) 97/1
AM2 Continuidade de fun¸oes vectoriais c˜ Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Uma fun¸˜o vectorial ´ cont´ ca e ınua num ponto se e s´ se todas o Limites as suas fun¸˜es coordenadas forem cont´ co ınuas nesse ponto. Continuidade Exerc´ ıcios: Estude quanto ` continuidade a fun¸˜o vectorial a ca f (x, y ) = (f1 (x, y ), f2 (x, y )) onde x5  se (x, y ) = (0, 0)  f1 (x, y ) = x2 + y2 1 se (x, y ) = (0, 0)  e f2 (x, y ) = cos(x + y ) 98/1
AM2 Fa¸a um esbo¸o das seguintes regi˜es c c o Fun¸˜es co 1 (x, y , z) ∈ R3 : x 2 + y 2 ≤ 3, −1 ≤ z ≤ 3, z ≥ 0 Dom´ ınio Linhas de n´ ıvel 2 (x, y , z) ∈ R3 : −9 ≤ − x 2 + y 2 , y ≥ 0 Topologia 3 (x, y , z) ∈ R3 : x 2 + y 2 ≤ z ≤ 4, y ≤ 0 Limites Continuidade 4 (x, y , z) ∈ R3 : x 2 + y 2 + z 2 ≤ 16, z ≤ 0, x ≥ 0 5 (x, y , z) ∈ R3 : x 2 + y 2 + z 2 ≤ 25, x ≤ 0, y ≤ 0, z ≤ 0 6 (x, y , z) ∈ R3 : x2 + y2 ≤ z ≤ 2 − x 2 + y 2, y ≥ 0 7 (x, y , z) ∈ R3 : x 2 + y 2 ≤ z 2 + 3, y ≤ x 8 (x, y , z) ∈ R3 : x2 + y2 ≤ z ≤ 5 − x 2 + y 2, y ≥ 0 9 (x, y , z) ∈ R3 : x 2 + y 2 ≥ 4, z ≥ x 2 + y 2 , z ≤ 9, x ≤ 0 99/1

Mais conteúdo relacionado

PDF
05a-integrais de linha
porSandra Gaspar Martins
 
PDF
Campos escalares e vetoriais - Cálculo 2
porSandra Gaspar Martins
 
PDF
04a-integrais duplos
porSandra Gaspar Martins
 
PDF
03 calculo diferencial-parte2
porSandra Gaspar Martins
 
PDF
03 calculo diferencial-parte1
porSandra Gaspar Martins
 
PDF
06-integrais de superfície
porSandra Gaspar Martins
 
PDF
04b-integrais triplos
porSandra Gaspar Martins
 
PDF
Iezzi24 35
porCarlos Campani
 
05a-integrais de linha
porSandra Gaspar Martins
 
Campos escalares e vetoriais - Cálculo 2
porSandra Gaspar Martins
 
04a-integrais duplos
porSandra Gaspar Martins
 
03 calculo diferencial-parte2
porSandra Gaspar Martins
 
03 calculo diferencial-parte1
porSandra Gaspar Martins
 
06-integrais de superfície
porSandra Gaspar Martins
 
04b-integrais triplos
porSandra Gaspar Martins
 
Iezzi24 35
porCarlos Campani
 

Mais procurados

PDF
30 lei inducao-faraday
porCarlos Augusto Pitombeira
 
PDF
Lei De InduçãO De Faraday
pordalgo
 
PDF
Editdocument15107902255388
porAssis Nunes
 
DOC
Cordas vibrantes
porCarlos Magno de Brito
 
PDF
Aula 1 integrais du e tr c_po_cci_ces
porGabriela Di Mateos
 
PDF
Cederj máximos e minimos multiplicadores de lagrange
porIgor Titara
 
PDF
Regra de simpson
porVera Gomes
 
PDF
Tccfinal
porabbeg
 
PDF
Integral de linha
porPolyanna Ferreira
 
PDF
Funcoesvetorias
porWillian Santana Quirino
 
PDF
Tensão média e tensão eficaz
porRodrigo Thiago Passos Silva
 
PDF
Aula 2 PROFMAT Aplicacoes da Inducao
porAline Guedes
 
PDF
Tarefa7
porLuan Gabriel
 
PDF
Resumo MD
porPedro Dias
 
PDF
Operadores
porCamila Soares
 
PDF
Aula10 diagramasde bode
porRicardo Carvalho
 
PDF
4 alternativas-para-resolver-a-equacao-de-schrodinger
porMarcelo de Souza
 
PDF
Aspectos de modelagem e imageamento usando equação da onda
porGrupo de Geofísica Computacional, UNICAMP
 
PDF
P2 calculo i_ (6)
porAndrei Bastos
 
PDF
Aula 10 profmat - congruencias lineares e quadraticas - 10 11-17
porAline Guedes
 
30 lei inducao-faraday
porCarlos Augusto Pitombeira
 
Lei De InduçãO De Faraday
pordalgo
 
Editdocument15107902255388
porAssis Nunes
 
Cordas vibrantes
porCarlos Magno de Brito
 
Aula 1 integrais du e tr c_po_cci_ces
porGabriela Di Mateos
 
Cederj máximos e minimos multiplicadores de lagrange
porIgor Titara
 
Regra de simpson
porVera Gomes
 
Tccfinal
porabbeg
 
Integral de linha
porPolyanna Ferreira
 
Funcoesvetorias
porWillian Santana Quirino
 
Tensão média e tensão eficaz
porRodrigo Thiago Passos Silva
 
Aula 2 PROFMAT Aplicacoes da Inducao
porAline Guedes
 
Tarefa7
porLuan Gabriel
 
Resumo MD
porPedro Dias
 
Operadores
porCamila Soares
 
Aula10 diagramasde bode
porRicardo Carvalho
 
4 alternativas-para-resolver-a-equacao-de-schrodinger
porMarcelo de Souza
 
Aspectos de modelagem e imageamento usando equação da onda
porGrupo de Geofísica Computacional, UNICAMP
 
P2 calculo i_ (6)
porAndrei Bastos
 
Aula 10 profmat - congruencias lineares e quadraticas - 10 11-17
porAline Guedes
 

Destaque

PDF
Cap09 primitivas2
porSandra Gaspar Martins
 
PDF
Tecnica de integracao resumo
porJoão Bastos
 
PDF
Derivadas Em Fisica I
porElisiofisico
 
PDF
Integral Substituicao Trigonometrica
porbtizatto1
 
PDF
08 derivadas
porRodrigo Oliveira
 
PDF
Movimentos da terra
porkarolpoa
 
PDF
Tectônica de placas
porkarolpoa
 
PDF
Projeções
porkarolpoa
 
PPTX
EQUAÇÃO DE TORRICELLI
porElisiofisico
 
PDF
Coordenadas geográficas
porkarolpoa
 
PDF
Minerais e rochas
porkarolpoa
 
DOCX
Aplicação das derivadas
pormeirellles
 
DOC
Questões Corrigidas, em Word: Vetores - Conteúdo vinculado ao blog http...
porRodrigo Penna
 
PPSX
Movimento Uniformemente Variado - Equação de Torricelli
porMarco Antonio Sanches
 
PDF
Apostila de mecânica aplicada
porCaio Cesar Cardoso
 
PDF
Fis01 cinemática escalar
porLucianoMadeira
 
DOC
Questões Corrigidas, em Word: Algarismos Significativos e Grandezas - Conteúd...
porRodrigo Penna
 
PDF
Aula 1 resultante de um sistema de forças
porFrancisco Netto
 
PDF
Mecânica Vetorial Para Engenheiros ( Solucionário Dinâmica )
poriuryanderson
 
PDF
Mecanica aplicada-apostila 2
porcristianorodcastro
 
Cap09 primitivas2
porSandra Gaspar Martins
 
Tecnica de integracao resumo
porJoão Bastos
 
Derivadas Em Fisica I
porElisiofisico
 
Integral Substituicao Trigonometrica
porbtizatto1
 
08 derivadas
porRodrigo Oliveira
 
Movimentos da terra
porkarolpoa
 
Tectônica de placas
porkarolpoa
 
Projeções
porkarolpoa
 
EQUAÇÃO DE TORRICELLI
porElisiofisico
 
Coordenadas geográficas
porkarolpoa
 
Minerais e rochas
porkarolpoa
 
Aplicação das derivadas
pormeirellles
 
Questões Corrigidas, em Word: Vetores - Conteúdo vinculado ao blog http...
porRodrigo Penna
 
Movimento Uniformemente Variado - Equação de Torricelli
porMarco Antonio Sanches
 
Apostila de mecânica aplicada
porCaio Cesar Cardoso
 
Fis01 cinemática escalar
porLucianoMadeira
 
Questões Corrigidas, em Word: Algarismos Significativos e Grandezas - Conteúd...
porRodrigo Penna
 
Aula 1 resultante de um sistema de forças
porFrancisco Netto
 
Mecânica Vetorial Para Engenheiros ( Solucionário Dinâmica )
poriuryanderson
 
Mecanica aplicada-apostila 2
porcristianorodcastro
 

Semelhante a 02 Campos Escalares e Vectoriais

PDF
01 eac proj vest mat módulo 1 função afim
porcon_seguir
 
PDF
Funcoes de varias variaveis calculo 2
porKassiane Campelo
 
DOC
Limites, derivadas e suas aplicações
porAfonso Celso Siqueira Silva
 
PDF
Questões - Bases Matemáticas
porRodrigo Thiago Passos Silva
 
PDF
Apostila derivadas
porEmerson Nascimento
 
PDF
Ex algebra (14)
porAndrei Bastos
 
PDF
Livrocalculo2 miolo
porresolvidos
 
PPTX
Funções e Função Afim
porestudamatematica
 
PDF
Apostila 001 trigonometria funcoes
porcon_seguir
 
PDF
Ex algebra (11)
porAndrei Bastos
 
PDF
Tarefa semana cinco
porCarla Restier
 
PDF
Questesdematemtica ano2003
porComputação Depressão
 
PPTX
Funções e Função Afim
porestudamatematica
 
PDF
Calculo1 aula05
porÉlica Dias
 
PDF
Calculo1 aula05
porCleide Soares
 
PDF
Derivadas
porSilvia Estrela
 
PDF
Ex algebra (8)
porAndrei Bastos
 
PDF
Mat funcoes 002 exercicios
portrigono_metrico
 
PDF
Cálculo Diferencial em R
portintintest
 
ODT
QUESTOES DE CÁLCULO
porJonathan Souza
 
01 eac proj vest mat módulo 1 função afim
porcon_seguir
 
Funcoes de varias variaveis calculo 2
porKassiane Campelo
 
Limites, derivadas e suas aplicações
porAfonso Celso Siqueira Silva
 
Questões - Bases Matemáticas
porRodrigo Thiago Passos Silva
 
Apostila derivadas
porEmerson Nascimento
 
Ex algebra (14)
porAndrei Bastos
 
Livrocalculo2 miolo
porresolvidos
 
Funções e Função Afim
porestudamatematica
 
Apostila 001 trigonometria funcoes
porcon_seguir
 
Ex algebra (11)
porAndrei Bastos
 
Tarefa semana cinco
porCarla Restier
 
Questesdematemtica ano2003
porComputação Depressão
 
Funções e Função Afim
porestudamatematica
 
Calculo1 aula05
porÉlica Dias
 
Calculo1 aula05
porCleide Soares
 
Derivadas
porSilvia Estrela
 
Ex algebra (8)
porAndrei Bastos
 
Mat funcoes 002 exercicios
portrigono_metrico
 
Cálculo Diferencial em R
portintintest
 
QUESTOES DE CÁLCULO
porJonathan Souza
 

Último

DOCX
Atividade de Extensão 2026.1 Cruzeiro do Sul
porProjeto Zero
 
PDF
MONDIM II - APONTAMENTOS PARA A HISTÓRIA DE S.CRISTÓVÃO DE MONDIM.pdf
porTeixeiraLopes3
 
PPTX
LINGUAGEM, LINGUA E FALA. LÍNGUA PORTUGUESA PARA ENSINO FUNDAMENTAL
porexpoentecoordenacao
 
PDF
3a-SERIE-LINGUA-PORTUGUESA- atividades de leitura e interpretação de textos e...
pormariza ferreira
 
PDF
Jogos expressao dramtica................
porVeronicaNeto1
 
PPTX
Teoria dos Conjuntos diagramas e programação
porPabloFirmino2
 
PPTX
MAIORES TERREMOTOS JÁ REGISTRADOS NA HISTÓRIA
porHenrique Pontes
 
PDF
a primavera da lagarta. Livro de Ruth Rocha.
porprofessorafabianaedu
 
PDF
Propostas de redações 1º Bimestre 2026 (3).pdf
porRosangelaTeixeira16
 
DOCX
quando as raízes curam a alma, restaurando a alma.docx
porJucyBordados
 
PPT
Proteínas_bioquímica_celular_aminoacidos_proteinas
porBiologia na Prática
 
PPTX
Introdução à Metodologia Científica.pptx
porThasLeal7
 
PDF
Caderno-1°-ano-3-trimestre-AVA-Linguagens.docx.pdf atividades diversas.
porprofecellnazario
 
PPTX
29303_e30e550ca2aa714c00e64f99347df19c.pptx
porantoniodvilacardoso
 
PPTX
Primeiros Socorros e Suporte Básico de Vida.pptx
porleonormartinscarmo
 
PDF
ORGANIZADOR CURRICULAR - 2026 - Formação Geral Básica - ENSINO MÉDIO.pdf
porssuser7076a8
 
PDF
BNCC ARTE - Ensino Fundamental I (1° ao 5° ano) habilidade 02 linha.pdf
porSheila de Souza
 
PDF
Organizador Curricular Base Comum 2026 - Ciências .pdf
porssuser7076a8
 
PPTX
cultura digital: tecnologia e sociedade no mundo contemporaneo
porlilianamachadoprof
 
PDF
Educacao especial cartilha p professores
porDiegoOliveiradeLemos
 
Atividade de Extensão 2026.1 Cruzeiro do Sul
porProjeto Zero
 
MONDIM II - APONTAMENTOS PARA A HISTÓRIA DE S.CRISTÓVÃO DE MONDIM.pdf
porTeixeiraLopes3
 
LINGUAGEM, LINGUA E FALA. LÍNGUA PORTUGUESA PARA ENSINO FUNDAMENTAL
porexpoentecoordenacao
 
3a-SERIE-LINGUA-PORTUGUESA- atividades de leitura e interpretação de textos e...
pormariza ferreira
 
Jogos expressao dramtica................
porVeronicaNeto1
 
Teoria dos Conjuntos diagramas e programação
porPabloFirmino2
 
MAIORES TERREMOTOS JÁ REGISTRADOS NA HISTÓRIA
porHenrique Pontes
 
a primavera da lagarta. Livro de Ruth Rocha.
porprofessorafabianaedu
 
Propostas de redações 1º Bimestre 2026 (3).pdf
porRosangelaTeixeira16
 
quando as raízes curam a alma, restaurando a alma.docx
porJucyBordados
 
Proteínas_bioquímica_celular_aminoacidos_proteinas
porBiologia na Prática
 
Introdução à Metodologia Científica.pptx
porThasLeal7
 
Caderno-1°-ano-3-trimestre-AVA-Linguagens.docx.pdf atividades diversas.
porprofecellnazario
 
29303_e30e550ca2aa714c00e64f99347df19c.pptx
porantoniodvilacardoso
 
Primeiros Socorros e Suporte Básico de Vida.pptx
porleonormartinscarmo
 
ORGANIZADOR CURRICULAR - 2026 - Formação Geral Básica - ENSINO MÉDIO.pdf
porssuser7076a8
 
BNCC ARTE - Ensino Fundamental I (1° ao 5° ano) habilidade 02 linha.pdf
porSheila de Souza
 
Organizador Curricular Base Comum 2026 - Ciências .pdf
porssuser7076a8
 
cultura digital: tecnologia e sociedade no mundo contemporaneo
porlilianamachadoprof
 
Educacao especial cartilha p professores
porDiegoOliveiradeLemos
 

02 Campos Escalares e Vectoriais

  • 1.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Campos escalares e vectoriais - Parte 1 Topologia Limites An´lise Matem´tica 2 a a Continuidade 2o Semestre 2011/12 Vers˜o de 16 de Maio de 2012 a 1/1
  • 2.
    AM2 Fun¸oes c˜ Fun¸˜es co Neste cap´ ıtulo trabalhamos com fun¸˜es co Dom´ ınio Linhas de n´ ıvel f : Rn −→ Rm (n, m ∈ N, n˜o simultˆneamente iguais a 1) a a Topologia Limites Se m = n = 1 estas fun¸˜es designam-se por fun¸˜es reais de co co Continuidade vari´vel real e foram estudadas em AM1. a f : R −→ R Se m = 1 estas fun¸˜es designam-se por campos escalares ou co fun¸˜es escalares. co f : Rn −→ R (n > 1) Se m > 1 estas fun¸˜es designam-se por campos vectoriais ou co fun¸˜es vectoriais. co f : Rn −→ Rm (n ≥ 1) 2/1
  • 3.
    AM2 Exemplos: Fun¸˜es co Dom´ ınio 1 f : D ⊂ R3 −→ R tal que f (x, y , z) = x + y + z Linhas de n´ ıvel Topologia 2 f : D ⊂ R2 −→ R4 tal que Limites x Continuidade f (x, y ) = x + y , x − y , xy , y 3 f : D ⊂ R2 −→ R tal que f (latitude, longitude) = (altitude) 4 f : D ⊂ R2 −→ R3 tal que f (latitude, longitude) = (altitude, humidade, temperatura) 5 f : D ⊂ R2 −→ R2 tal que f (latitude, longitude) = vector que indica a direc¸˜o e intensidade do vento ca 6 f : D ⊂ R3 −→ R3 tal que f (x, y , z) = vector que indica a direc¸˜o de escoamento de um flu´ em ca ıdo movimento 3/1
  • 4.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 4/1
  • 5.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 5/1
  • 6.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 6/1
  • 7.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 7/1
  • 8.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 8/1
  • 9.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 9/1
  • 10.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 10/1
  • 11.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 11/1
  • 12.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 12/1
  • 13.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 13/1
  • 14.
    AM2 Dado o campo vectorial Fun¸˜es co Dom´ ınio f : R2 −→ R4 Linhas de n´ ıvel Topologia x Limites f (x, y ) = xy , x 2 − y , x − 3y , √ Continuidade y ´ composto por 4 fun¸˜es componentes ou fun¸˜es e co co coordenadas que s˜o: a f1 (x, y ) = xy f2 (x, y ) = x 2 − y f3 (x, y ) = x − 3y x f4 (x, y ) = √ y Nota: estas fun¸˜es s˜o campos escalares. co a 14/1
  • 15.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Fa¸a um esbo¸o do gr´fico das seguintes fun¸˜es: c c a co Linhas de n´ ıvel Topologia 1 f (x, y ) = 5 Limites 2 f (x, y ) = x Continuidade 3 f (x, y ) = x + y 4 f (x, y ) = y 2 5 f (x, y ) = 2 + cos(x) 6 f (x, y ) = x 2 + y 2 7 f (x, y ) = − x 2 + y 2 + 3 8 f (x, y ) = − x 2 + y 2 + 3 9 f (x, y ) = 9 − x2 − y2 √ 10 f (x, y ) = − 25 − x 2 15/1
  • 16.
    AM2 Dom´ ınio Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o (Dom´ de uma fun¸˜o) ca ınio ca Limites Dada uma fun¸˜o f : Rn −→ Rm (n, m ≥ 1) define-se o ca Continuidade dom´ınio de f por Df = {x ∈ Rn : ∃1 y ∈ IR m , f (x) = y } Exemplo: x f : D ⊂ R2 −→ R4 tal que f (x, y ) = x + y , x − y , xy , y tem como dom´ D = {(x, y ) ∈ R2 : y = 0} ınio 16/1
  • 17.
    AM2 1 ⇒ a ∈ R {0} Fun¸˜es co a √ Dom´ ınio a ⇒ a ∈ R+ 0 Linhas de n´ ıvel ln(a) ⇒ a ∈ R+ Topologia Limites |a| ⇒ a ∈ R Continuidade an ⇒ a ∈ R (n ∈ N) cos(a) ⇒ a ∈ R sin(a) ⇒ a ∈ R π tan(a) ⇒ a ∈ R + kπ, k ∈Z 2 arccos(a) ⇒ a ∈ [−1, 1] arcsin(a) ⇒ a ∈ [−1, 1] arctan(a) ⇒ a ∈ R ... 17/1
  • 18.
    AM2 Fun¸˜es co Determine o dom´ das seguintes fun¸˜es e represente-o ınio co Dom´ ınio geometricamente: Linhas de n´ ıvel 1 f (x, y ) = (ln(x), ln(y ), x − y ) Topologia x Limites 2 f (x, y ) = y Continuidade 3 f (x, y ) = √ 1 2 2 4−x −y √ 4 f (x, y ) = ( −x 2 + 1, 4 − y 2) −3 5 f (x, y , z) = ( √ , ze x , y ) x 2 +y 2 +z 2 −9 √ 6 f (x, y ) = arcsin( x ) + xy 2 7 f (x, y ) = ln( x−y ) 2x 8 f (x, y ) = y − 2x 2 18/1
  • 19.
    AM2 Linhas e Superf´ ıcies de N´ ıvel Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Seja f : R2 −→ R chama-se curva ou linha de n´ k ao ıvel Limites Continuidade conjunto: Nk = {(x, y ) ∈ R2 : k = f (x, y ), (x, y ) ∈ Df } (k ∈ Df ) Se f : R3 −→ R chama-se superf´ de n´ k ao ıcie ıvel conjunto: Nk = {(x, y , z) ∈ R3 : k = f (x, y , z), (x, y , z) ∈ Df } (k ∈ Df ) http://www.flashandmath.com/mathlets/multicalc/contours/index.html 19/1
  • 20.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 20/1
  • 21.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 21/1
  • 22.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 22/1
  • 23.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 23/1
  • 24.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 24/1
  • 25.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 25/1
  • 26.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 26/1
  • 27.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 27/1
  • 28.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Calcule algumas linhas de n´ das fun¸˜es que se seguem at´ ıvel co e Topologia conseguir fazer um esbo¸o do gr´fico da fun¸˜o: c a ca Limites 1 f (x, y ) = xy Continuidade 2 f (x, y ) = x 2 − y 2 3 f (x, y ) = y − cos(x) 1 4 f (x, y ) = e x 2 +y 2 5 f (x, y ) = ln(x 2 + y 2 ) 6 f (x, y ) = |x| + |y | 7 f (x, y , z) = x2 + y2 − z2 (ver figuras) 28/1
  • 29.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 29/1
  • 30.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 30/1
  • 31.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 31/1
  • 32.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 32/1
  • 33.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 33/1
  • 34.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 34/1
  • 35.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 35/1
  • 36.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 36/1
  • 37.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 37/1
  • 38.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 38/1
  • 39.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 39/1
  • 40.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 40/1
  • 41.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 41/1
  • 42.
    AM2 Distˆncia a Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o (Distˆncia) ca a Limites Continuidade Dados dois pontos de Rn , P = (x1 , ..., xn ) e P = (x1 , ...xn ) a distˆncia euclideana entre eles ´ dada por a e d(P, P ) = (x1 − x1 )2 + (x2 − x2 )2 + ... + (xn − xn )2 −→ − Nota: d(P, P ) = ||PP || ´ a norma ou comprimento do vector e −→ − PP . 42/1
  • 43.
    AM2 Bola aberta ou Vizinhan¸a c Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Defini¸˜o (Bola aberta ou Vizinhan¸a) ca c Continuidade Diz-se vizinhan¸a ε de um ponto a ∈ Rn (Bola aberta de c centro em a e raio ε) ao conjunto Bε (a) = {x ∈ Rn : d(x, a) < ε} ou Bε (a) = {x ∈ Rn : ||x − a|| < ε}. 43/1
  • 44.
    AM2 Fun¸˜es co Dom´ ınio Calcule: Linhas de n´ ıvel B5 (3) = Topologia Limites Continuidade B2 (2, −3) = B3 (1, 2, 3) = 44/1
  • 45.
    AM2 Defini¸˜o ca Seja a ∈ Rn e X ⊂ Rn . Fun¸˜es co Dom´ ınio a ´ interior a X se e Linhas de n´ ıvel Topologia ∃ε : Bε (a) ⊂ X ; Limites Continuidade se existe uma Bola de centro em a toda contida em X . a ´ exterior a X se e ∃ε : Bε (a) ⊂ Rn X ; se existe uma Bola de centro a que n˜o tem pontos de X . a a ´ fronteiro a X se ∀ε > 0 e Bε (a) ∩ X = ∅ e Bε (a) ∩ (Rn X ) = ∅, se qualquer Bola de centro em a tem pontos de X e de Rn X . 45/1
  • 46.
    AM2 Defini¸˜o ca Fun¸˜es co Seja a ∈ Rn e X ⊂ Rn . Dom´ ınio Linhas de n´ ıvel a ´ ponto de acumula¸˜o de X se e ca Topologia Limites ∀ε > 0, Bε (a) ∩ (X {a}) = ∅; Continuidade se qualquer vizinhan¸a de a tem infinitos pontos de X c distintos de a. a ´ ponto isolado de X se e ∃ε > 0, : Bε (a) ∩ X = {a}; se existe uma Bola de centro em a que o unico ponto que ´ tem de X ´ o pr´prio a. e o a ´ aderente a X se a ∈ X ou a ∈ fr (X ) e 46/1
  • 47.
    AM2 Defini¸˜o ca Fun¸˜es co Interior de X : int(X ) ´ o conjunto dos pontos interiores e Dom´ ınio Linhas de n´ ıvel aX Topologia Exterior de X :ext(X ) ´ o conjunto dos pontos exteriores e Limites aX Continuidade Fronteira de X : fr (X ) ´ o conjunto dos pontos fronteiros e de X Derivado de X : X ´ o conjunto dos pontos de e acumula¸˜o de X ca ¯ e Aderˆncia de X : X ´ o conjunto dos pontos aderentes a e X Teorema int(X ) ∪ ext(X ) ∪ fr (X ) = Rn e s˜o disjuntos 2 a 2 a 47/1
  • 48.
    AM2 Fun¸˜es co Defini¸˜o ca Dom´ ınio Um conjunto X de Rn ´ e Linhas de n´ ıvel Topologia aberto se X = int(X ) (⇔ X ∩ fr (x) = ∅) Limites ¯ fechado se X = X (⇔ fr (X ) ⊂ X ) Continuidade limitado se existir uma bola que o contenha. compacto se for limitado e fechado. Nota: Existem conjuntos que n˜o s˜o abertos nem fechados a a ∅ e Rn s˜o abertos e fechados. a 48/1
  • 49.
    AM2 Seja X o conjunto de R2 colorido a vermelho: Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade Complete: { } ∈ int(X ) { } ∈ ext(X ) { } ∈ fr (X ) { }∈X { ¯ }∈X { } ∈ Pontos Isolados de X 49/1
  • 50.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel 1 Classifique topologicamente os conjuntos: Topologia 1 A = (x, y ) ∈ R2 : −x 2 + 1 < y < −2x 2 + 2 Limites 2 B = (x, y ) ∈ R2 : |x| ≤ 1 ∧ |y | ≤ e x Continuidade 3 C = (x, y ) ∈ R2 : (x 2 + y 2 − 1)(4 − x 2 − y 2 ) > 0 2 Calcule o dom´ ınio, Df , das seguintes fun¸˜es. Represente co geometricamente e classifique topologicamente Df . 1 f (x, y ) = x(1 − |y |) x 2 +y 2 (x, y ) = (0, 0) 2 f (x, y ) = x−y 1 (x, y ) = (0, 0) x 3 f (x, y ) = ln( y ) + arcsin(x 2 + y 2 ) 4 f (x, y ) = ln(y − x) 9 − x 2 − (y + 1)2 50/1
  • 51.
    AM2 Limite Fun¸˜es co Defini¸˜o (Limite de campo escalar definido em R2 ) ca Dom´ ınio Linhas de n´ ıvel Seja f : Df ⊆ R2 −→ R e (x0 , y0 ) um ponto de acumula¸˜o do ca Topologia dom´ Df . ınio Limites O limite de f (x, y ) quando (x, y ) tende para (x0 , y0 ) ´ l, e e Continuidade escreve-se lim f (x, y ) = l (x,y )→(x0 ,y0 ) se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀(x, y ) ∈ Df {(x0 , y0 )}, (x, y ) ∈ Bε (x0 , y0 ) =⇒ f (x, y ) ∈ Bδ (l) ou seja, (x − x0 )2 + (y − y0 )2 < ε =⇒ |f (x, y ) − l| < δ) 51/1
  • 52.
    AM2 Geometricamente Fun¸˜es co Este limite implica que, Dom´ ınio para qualquer ponto (x, y ) = (x0 , y0 ) do dom´ de f , ınio Linhas de n´ ıvel no disco de raio ε, Topologia o valor de f (x, y ) esteja entre os planos de equa¸˜o z = l − δ e ca Limites z = l + δ, Continuidade ou seja, todos contidos no cilindro de raio ε e altura 2δ. 52/1
  • 53.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 53/1
  • 54.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 54/1
  • 55.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 55/1
  • 56.
    AM2 Exemplo: Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Vejamos se Topologia lim 5+4 x2 + y2 = 5 (x,y )→(0,0) Limites Continuidade ou seja, vejamos se ∀δ > 0, ∃ε(δ) > 0 : ∀(x, y ) ∈ Df {(0, 0)}, (x, y ) ∈ Bε (0, 0) =⇒ f (x, y ) ∈ Bδ (5) ou seja, (x − 0)2 + (y − 0)2 < ε =⇒ |f (x, y ) − 5| < δ) 1 1 Determine ε sendo δ = 10, δ = 10 , δ= 100 , δ qualquer... 56/1
  • 57.
    AM2 Revis˜es: o |ab| = |a| |b| a |a| Fun¸˜es co = Dom´ ınio b |b| Linhas de n´ ıvel |a + b| ≤ |a| + |b| Topologia Limites Continuidade ab = |a|b √ |a| = a2 |a| ≤ a2 + b 2 a2 0≤ ≤1 a2 + b2 | sin(a)| ≤ 1 π | arctan(a)| ≤ 2 57/1
  • 58.
    AM2 Exerc´ ıcios: I Fun¸˜es co Dom´ ınio Mostre, por defini¸˜o de limite, que: ca Linhas de n´ ıvel 1 lim f (x, y ) = 0 onde f (x, y ) = 3 x 2 + y 2 cos(xy ) (x,y )→(0,0) Topologia Limites Continuidade 2 lim f (x, y ) = 0 onde (x,y )→(0,0) f (x, y ) = 2 sin(x + y ) x 2 + y 2 3 lim f (x, y ) = 7 onde f (x, y ) = 2x + y (x,y )→(2,3) 4 lim x =2 (x,y )→(2,1) 5 lim 4xy = 0 (x,y )→(0,0) 58/1
  • 59.
    AM2 Exerc´ ıcios: II Fun¸˜es co x 2y 2 6 lim = 0 (ver fig.) Dom´ ınio (x,y )→(0,0) x2 + y2 Linhas de n´ ıvel Topologia 4x 3 Limites 7 lim =0 Continuidade (x,y )→(0,0) x 2 + y2 1 8 lim = 0 (se poss´ - ver fig.) ıvel (x,y )→(0,0) x 2 + y2 x 4 + 2y 3 9 lim =0 (x,y )→(0,0) x 2 + y 2 y 10 lim xy sin( ) = 0 (x,y )→(0,0) x 59/1
  • 60.
    AM2 Exerc´ ıcios: III Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 11 lim (x 2 + y 2 ) arctan(xy ) = 0 (x,y )→(0,0) 60/1
  • 61.
    AM2 Limite Fun¸˜es co Dom´ ınio Defini¸˜o (Limite de campo escalar definido em Rn ) ca Linhas de n´ ıvel Seja f : Df ⊆ Rn −→ R e a um ponto de acumula¸˜o do ca Topologia dom´ Df . ınio Limites O limite de f (x) quando x tende para a ´ l, e escreve-se e Continuidade lim f (x) = l x→a se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀x ∈ Df {a}, x ∈ Bε (a) =⇒ f (x) ∈ Bδ (l) ou seja, (x1 − a1 )2 + ...(xn − an )2 < ε =⇒ |f (x) − l| < δ) 61/1
  • 62.
    AM2 Proposi¸˜o (Propriedades dos limites) ca Fun¸˜es co Sejam f : Df ⊆ Rn −→ R e g : Dg ⊆ Rn −→ R duas fun¸˜es co Dom´ ınio escalares e a um ponto de acumula¸˜o de Df ∩ Dg . ca Linhas de n´ ıvel Se limx→a f (x) = l1 e limx→a g (x) = l2 ent˜o a Topologia Limites O limite ´ unico. e´ Continuidade lim (f (x) + g (x)) = l1 + l2 x→a lim (f (x).g (x)) = l1 .l2 x→a f (x) l1 lim = x→a g (x) l2 lim (cf (x)) = c.l1 x→a 62/1
  • 63.
    AM2 Limite relativo Fun¸˜es co Dom´ ınio Defini¸˜o (Limite relativo a um conjunto) ca Linhas de n´ ıvel Topologia Seja S um subconjunto de Df , f : Df ⊆ Rn −→ R e a um Limites ponto de acumula¸˜o do dom´ Df . O limite de f (x) ca ınio Continuidade relativo a S quando x tende para a ´ l, e escreve-se e lim f (x) = l x→a x∈S se e s´ se o ∀δ > 0, ∃ε(δ) > 0 : ∀x ∈ S {a}, x ∈ Bε (a) =⇒ f (x) ∈ Bδ (l) No caso em que S = (x, y ) ∈ R2 : y = mx + b a estes limites chamam-se os limites direccionais. 63/1
  • 64.
    AM2 Fun¸˜es co Dom´ ınio Proposi¸˜o ca Linhas de n´ ıvel Se o limite existir ent˜o o limite relativo a qualquer conjunto a Topologia existe e tem o mesmo valor. Limites Continuidade Exerc´ ıcio: Que pode concluir se encontrar dois limites relativos diferentes? iguais? 64/1
  • 65.
    AM2 Exerc´ ıcios Fun¸˜es co Utilize limites relativos para estudar os limites: Dom´ ınio x2 1 lim (ver fig.) (x,y )→(0,0) x 2 + y 2 Linhas de n´ ıvel Topologia Limites xy Continuidade 2 lim (ver fig.) (x,y )→(0,0) x 2 + y2 x 3 lim (ver fig.) (x,y )→(0,0) x 2 + y2 x −y 4 lim (x,y )→(0,0) x + y 4xy 5 lim (x,y )→(0,0) x 2+ y2 xy 2 6 lim(x,y )→(0,0) (x+y 2 )2 65/1
  • 66.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 66/1
  • 67.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 67/1
  • 68.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 68/1
  • 69.
    AM2 Limites e propriedades Fun¸˜es co Dom´ ınio Defini¸˜o (Limites iterados ou sucessivos) ca Linhas de n´ ıvel Topologia Seja f : Df ⊂ R2 −→ R e (a, b) um ponto de acumula¸˜o do ca Limites dom´ Df , ent˜o os limites ınio a Continuidade lim lim f (x, y ) , lim lim f (x, y ) x→a y →b y →b x→a dizem-se limites iterados ou sucessivos. Nota: o caso geral, de uma fun¸˜o definida em Rn , ´ ca e limx1 →a1 (· · · (limxn →an f (x1 , · · · , xn ))). Proposi¸˜o ca Se dois limites iterados forem diferentes (existirem e forem finitos) ent˜o n˜o existe limite. a a 69/1
  • 70.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Utilize limites iterados para estudar os limites: Continuidade x − 2y 1 lim (x,y )→(0,0) x + y 4xy 2 lim (x,y )→(0,0) (x 2 + y 2 )5 70/1
  • 72.
    AM2 Exerc´ ıcios Globais de Limites I Fun¸˜es co Dom´ ınio Estude a existˆncia dos seguintes limites. e Linhas de n´ ıvel x 4 + 2y 2 Topologia 1 lim (x,y )→(0,0) x 2 + y 2 Limites Continuidade y2 2 lim (x,y )→(0,0) x 2 + y2 x 2y 3 lim (x,y )→(0,0) (x 2 + y 2 )2 y −2 4 lim (x,y )→(−3,2) x + 3 72/1
  • 73.
    AM2 Exerc´ ıcios Globais de Limites II Fun¸˜es co xy + 3 5 lim Dom´ ınio (x,y )→(0,0) 1 − 2x 2 Linhas de n´ ıvel Topologia xy 2 Limites 6 lim (x,y )→(0,0) x 2 + y 4 Continuidade 1 7 lim x sin (x,y )→(0,0) y xy 8 lim (x,y )→(0,0) x 2 + 3y 2 x 2y 9 lim (x,y )→(0,0) (x 2 + y )2 73/1
  • 74.
    AM2 Exerc´ ıcios Globais de Limites III Fun¸˜es co x 4y Dom´ ınio 10 lim (x,y )→(0,0) y 3 − x 6 Linhas de n´ ıvel Topologia Limites x 2y 11 lim Continuidade (x,y )→(0,0) (y + x 2 )2 x +y −2 12 lim (x,y )→(1,1) x −y 13 limite de f nos pontos (0, 0); (1, 1); (1, 0); (0, 1), sendo   1 − 2y + x se x + y < 1 f (x, y ) = 1 se x + y = 1 2 − x + y se x + 1 > 1.  74/1
  • 75.
    AM2 Exerc´ ıcios Globais de Limites IV Fun¸˜es co Dom´ ınio 14 limite de f nos pontos (1, 1); (−1, 0); (0, 2), sendo Linhas de n´ ıvel  Topologia  x +y se x > 0 Limites f (x, y ) = 2 se x = 0 x − y + 2 se x < 0.  Continuidade 15 indique para que pontos da recta y = −x existe limite de f , sendo   1 − 2y + x se x + y < 0 f (x, y ) = 4 se x + y = 0 6−x +y se x + 1 > 0.  75/1
  • 76.
    AM2 Exerc´ ıcios Globais de Limites V Fun¸˜es co Dom´ ınio 16 limite de f nos pontos (1, 2); (2, 1); (2, 2), sendo Linhas de n´ ıvel Topologia 2x − y se y < x f (x, y ) = Limites x2 se y ≥ x. Continuidade 17 lim g (x, y ) e lim g (x, y ) onde (x,y )→(0,0) (x,y )→(0,2)  4−x 2 −y 2  e se x 2 + y 4 ≥ 4 g (x, y ) = e se (x, y ) = (0, 0) 1 se x 2 + y 2 < 4  x 2 +y 2 76/1
  • 77.
    AM2 Exerc´ ıcios Globais de Limites VI Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites 18 lim f (x, y ) onde Continuidade (x,y )→(0,−4) x2 x 2 +(y +4)2 se (x, y ) = (0, −4) f (x, y ) = 1 se (x, y ) = (0, −4) 77/1
  • 78.
    AM2 Limite Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o (Limite de fun¸˜es vectoriais) ca co Topologia Seja Limites Continuidade f : Df ⊆ Rn −→ Rm x −→ y = f (x) = (f1 (x), ..., fm (x)) e a um ponto de acumula¸˜o do dom´ Df =D ca ınio . f1 ∩Df2 ∩...∩Dfm O limite de f (x) quando x tende para a ´ um vector de m e coordenadas onde cada uma corresponde ao limite da fun¸˜o ca coordenada respectiva. Assim lim f (x) = lim f1 (x), ... lim fm (x) x→a x→a x→a 78/1
  • 79.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade Calcule: 1 lim f (x, y ) onde f (x, y ) = (x 2 , xy 2 ) (x,y )→(1,2) 3xy 2 lim f (x, y ) onde f (x, y ) = ln(4 − x 2 − y 2 ), x 2 +y 2 (x,y )→(0,0) 79/1
  • 80.
    AM2 Fun¸˜o composta (campos ca Fun¸˜es co escalares) Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Sejam g : Dg ⊆ Rn −→ R e f : Df ⊆ R −→ R duas fun¸˜es co Limites escalares. Define-se a fun¸˜o composta de f com g como ca Continuidade f : D ⊆ Rn −→ R x −→ (f ◦ g )(x) = f (g (x)) sendo D = {x ∈ Rn : x ∈ Dg ∧ g (x) ∈ Df } 80/1
  • 81.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites √ Continuidade 1 Seja f (t) = t e g (x, y ) = x 2 + y 2 + 2. Calcule (f ◦ g )(1, 3), (f ◦ g )(1, 1) e (f ◦ g )(x, y ). 2 Seja f (t) = t 3 e g (x, y ) = x − 4y . Calcule (f ◦ g )(1, 3), (f ◦ g )(1, 1) e (f ◦ g )(x, y ). 81/1
  • 82.
    AM2 Fun¸˜o composta (campos ca Fun¸˜es co vectoriais) Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Sejam g : Dg ⊆ Rn −→ Rp e f : Df ⊆ Rp −→ Rm duas Limites fun¸˜es vectoriais. Define-se a fun¸˜o composta de f com g co ca Continuidade como f ◦ g : D ⊆ Rn −→ Rm x −→ (f ◦ g )(x) = f (g (x)) sendo D = x ∈ Rn : x ∈ Dg ∧ g (x) ∈ Df 82/1
  • 83.
    AM2 Exerc´ ıcios Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites 1 Seja f (u, v ) = (e u , e v ) e g (x, y , z) = (x 2 + 2y 2 + z 2 , xyz). Continuidade Calcule, se existir, (f ◦ g )(1, 2, 3), (f ◦ g )(1, 1, 1), (f ◦ g )(x, y , z) e (g ◦ f )(x, y ). 2 Seja f (u, v ) = (u + v , u − v , uv ) e g (x, y , z) = (xy , yz). Calcule, se exisitir, (f ◦ g )(1, 2, 3), (f ◦ g )(1, 1, 1), (f ◦ g )(x, y , z) e (g ◦ f )(x, y ). 83/1
  • 84.
    AM2 Continuidade Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Defini¸˜o ca Limites Seja f : Df ⊂ Rn −→ R, e a um ponto de Df . Diz-se que f ´ e Continuidade cont´ınua em a se e s´ o ∃ lim f (x) e lim f (x) = f (a) x→a x→a Defini¸˜o ca f diz-se cont´ ınua num dado conjunto S se f ´ cont´ e ınua em todos os pontos de S. Nota: Se S = Df diz-se simplesmente que f ´ cont´ e ınua. 84/1
  • 85.
    AM2 Propriedades das fun¸˜es co Fun¸˜es co cont´ ınuas Dom´ ınio Linhas de n´ ıvel Proposi¸˜o ca Topologia Limites Sejam f e g duas fun¸˜es escalares com dom´ contido em co ınio Continuidade Rn e cont´ ınuas em a. Ent˜o, a f f + g, f − g, f .g e (g (a) = 0) g s˜o cont´ a ınuas em a. Proposi¸˜o ca Sejam g : Dg ⊆ Rn −→ R cont´ ınua em a e f : Df ⊆ R −→ R cont´ ınua em g (a). Ent˜o a f ◦ g ´ cont´ e ınua em a. 85/1
  • 86.
    AM2 Exerc´ ıcios I Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Estude quanto ` continuidade:1 (ver figuras) a Topologia 1 Limites x2 + sin(x + y ) − e cos(y ) f (x, y ) = Continuidade x −3 2  2xy se (x, y ) = (0, 0)  f (x, y ) = x2+ y2  0 se (x, y ) = (0, 0) 3 xy 2  se (x, y ) = (0, 0)  f (x, y ) = x2 + y2 0 se (x, y ) = (0, 0)  86/1
  • 87.
    AM2 Exerc´ ıcios II Fun¸˜es co 4  xy x 2 − y 2  Dom´ ınio Linhas de n´ ıvel se (x, y ) = (0, 0) f (x, y ) = x2 + y2 Topologia 0 se (x, y ) = (0, 0)  Limites Continuidade 5   2x + 3y se x = y f (x, y ) = x −y  5 se x = y 6   xy + 1 se y = x 2 f (x, y ) = x2 − y  0 se y = x 2 7 1 − x 2 − y 2 se x 2 + y 2 ≤ 1 f (x, y ) = 0 se x 2 + y 2 > 1 87/1
  • 88.
    AM2 Exerc´ ıcios III Fun¸˜es co 8 Dom´ ınio x +y se x = y Linhas de n´ ıvel f (x, y ) = 0 se x = y Topologia Limites 9 xy Continuidade se x 2 = y 2 f (x, y ) = x2 − y2 0 se x 2 = y 2 10 (x − 1)y 2  se (x, y ) = (1, 0)  f (x, y ) = (x − 1)2 + y 2 10 se (x, y ) = (1, 0)  11 x + y se y ≤ x 2 f (x, y ) = 3x − 1 se y > x 2 88/1
  • 89.
    AM2 Exerc´ ıcios IV Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia 12 Limites e y − 2x se y ≤ 2x Continuidade f (x, y ) = ln(y − 2x) se y > 2x 13   1 − 2y + x se y + x < 0 f (x, y ) = 4 se y + x = 0 6−x +y se y + x > 0  1 Pode confirmar usando http://math.hws.edu/xFunctions/ 89/1
  • 90.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 90/1
  • 91.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 91/1
  • 92.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 92/1
  • 93.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 93/1
  • 94.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 94/1
  • 95.
    AM2 Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Limites Continuidade 95/1
  • 96.
    AM2 Prolongamento cont´ ınuo Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Uma fun¸˜o f : Df ⊂ Rn −→ R diz-se prolong´vel por ca a Topologia continuidade ao ponto a ( a ∈ Df ), Limites se e s´ se o Continuidade a ∈ Df e existe lim f (x) . (x)→a O Prolongamento (cont´ ınuo) de f a a ´ e f (x) se x ∈ Df f (x) = lim f (x) se x = a x→a Nota: esta fun¸˜o ´ cont´ ca e ınua. 96/1
  • 97.
    AM2 Exerc´ ıcios I Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Topologia Determine, se existirem, prolongamentos cont´ ınuos de: Limites 1 − 1 f (x, y ) = e x 2 +y 2 Continuidade 1 2 f (x, y ) = x 2 cos x 2 +y 2 x 2y 3 f (x, y ) = x 4 +y −sin(x) ao ponto (0, 0) x2 4 f (x, y ) = x 3 +y −tan(x) ao ponto (0, 0) x 3 cos(y )+y 3 cos(x) 5 f (x, y ) = x 2 +y 2 ao ponto (0, 0) 97/1
  • 98.
    AM2 Continuidade de fun¸oes vectoriais c˜ Fun¸˜es co Dom´ ınio Linhas de n´ ıvel Defini¸˜o ca Topologia Uma fun¸˜o vectorial ´ cont´ ca e ınua num ponto se e s´ se todas o Limites as suas fun¸˜es coordenadas forem cont´ co ınuas nesse ponto. Continuidade Exerc´ ıcios: Estude quanto ` continuidade a fun¸˜o vectorial a ca f (x, y ) = (f1 (x, y ), f2 (x, y )) onde x5  se (x, y ) = (0, 0)  f1 (x, y ) = x2 + y2 1 se (x, y ) = (0, 0)  e f2 (x, y ) = cos(x + y ) 98/1
  • 99.
    AM2 Fa¸a um esbo¸o das seguintes regi˜es c c o Fun¸˜es co 1 (x, y , z) ∈ R3 : x 2 + y 2 ≤ 3, −1 ≤ z ≤ 3, z ≥ 0 Dom´ ınio Linhas de n´ ıvel 2 (x, y , z) ∈ R3 : −9 ≤ − x 2 + y 2 , y ≥ 0 Topologia 3 (x, y , z) ∈ R3 : x 2 + y 2 ≤ z ≤ 4, y ≤ 0 Limites Continuidade 4 (x, y , z) ∈ R3 : x 2 + y 2 + z 2 ≤ 16, z ≤ 0, x ≥ 0 5 (x, y , z) ∈ R3 : x 2 + y 2 + z 2 ≤ 25, x ≤ 0, y ≤ 0, z ≤ 0 6 (x, y , z) ∈ R3 : x2 + y2 ≤ z ≤ 2 − x 2 + y 2, y ≥ 0 7 (x, y , z) ∈ R3 : x 2 + y 2 ≤ z 2 + 3, y ≤ x 8 (x, y , z) ∈ R3 : x2 + y2 ≤ z ≤ 5 − x 2 + y 2, y ≥ 0 9 (x, y , z) ∈ R3 : x 2 + y 2 ≥ 4, z ≥ x 2 + y 2 , z ≤ 9, x ≤ 0 99/1