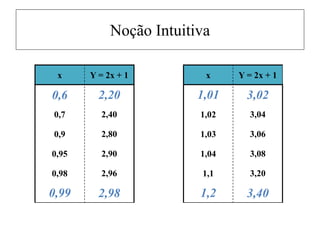
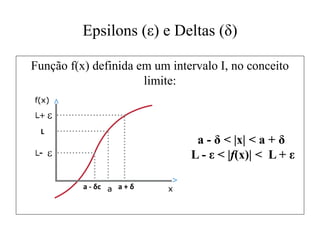
O documento apresenta uma introdução aos conceitos fundamentais do cálculo diferencial e integral. Em três frases ou menos, resume-se: O texto define limites de funções de forma intuitiva e por meio de símbolos, apresenta noções sobre derivadas, incluindo a taxa de variação instantânea e a condição de derivabilidade. Também aborda teoremas como o do valor médio e do valor extremo, importantes para a otimização de funções.

1. CENTRO SUPERIOR DE ESTUDOS DE
MANHUAÇU
Cálculo Diferencial e Integral
Matemática
M. Sc. Lima Deleon Martins (deleon_lima@hotmail.com)
Manhuaçu - MG
2011/2

3. Introdução intuitiva
Incógnita que "tende" a ser um determinado número, ou
seja, no limite, esta incógnita nunca vai ser o número,
mas vai se aproximar muito, de tal maneira que não se
consiga estabelecer uma distância que vai separar o
número da incógnita.
“número para o qual y = f(x) difere arbitrariamente
muito pouco quando o valor de x difere de x0
arbitrariamente muito pouco também”

4. Introdução intuitiva



1
2
lim
3
x
x
f(x) = 2x + 1

5. Noção Intuitiva
Daremos valores a x que se aproximem de 1, pela sua
direita (valores maiores que 1) e pela sua esquerda
(valores menores que 1) para calcularmos o valores
correspondentes de y:
f(x)= 2x + 1

6. Noção Intuitiva
x Y = 2x + 1 x Y = 2x + 1
0,6 2,20 1,01 3,02
0,7 2,40 1,02 3,04
0,9 2,80 1,03 3,06
0,95 2,90 1,04 3,08
0,98 2,96 1,1 3,20
0,99 2,98 1,2 3,40

7. Noção intuitiva
Se x=0,98 então: y = f(x) = 2,96
Se x=0,998 então: y = f(x ) = 2,996
Se x=0,9998 então: y = f(x) = 2,9996
Se x=0,99999 então: y = f(x )= 2,99998



1
2
lim
1
x
x
f(x) = 2x + 1

8. Noção Intuitiva
A medida que x se aproxima de 1, y se aproxima de 3,
ou seja, quando x tende para 1 (x → 1), y tende para
3 (y → 3), ou seja:
3
1
2
lim
3



x
x

9. Símbolos

11. Aproximação de x  f (x)
x f(x)= 2x + 4 x-2 y-8
1,9 7,8 -0,1 -0,2
1,99 7,98 -0,01 -0,02
1,999 7,998 -0,001 -0,002
⁞ ⁞ ⁞ ⁞
2,001 8,002 0,001 0,002
2,01 8,02 0,01 0,02
2,1 8,2 0,1 0,2

12. Aproximação de x  f (x)
|x-2| =0,1 |y-8| =0,2
|x-2| =0,01 |y-8| =0,02
|x-2| =0,001 |y-8| =0,002
⁞ ⁞
|x-2| =0,001 |y-8| =0,002
|x-2| =0,01 |y-8| =0,02
|x-2| =0,1 |y-8| =0,2
Quando x se aproxima cada vez mais de 2, f (x) aproxima-se
cada vez mais de 8.

13. Epsilons (ε) e Deltas (δ)
Observemos que podemos tornar f(x) tão próximos de 8
quanto desejarmos, bastando para isto tomarmos x
suficientemente próximo de 2.
De forma técnica a diferença entre f(x) e 8 ( |f(x) - 8|) é
reduzida, desde que o módulo da diferença entre x e 2 (
|x - 2 |) seja suficientemente pequeno.

14. Epsilons (ε) e Deltas (δ)
A matemática utiliza as letras gregas ε (epsilon) e δ
(delta) para indicar essas pequenas diferenças.
Assim, dado um número positivo δ, se desejarmos |f(x)
- 8| menor que ε, devemos tomar |x - 2| suficientemente
pequeno, isto é, devemos encontrar um número positivo
δ, suficientemente pequeno:

15. Epsilons (ε) e Deltas (δ)
Assim, dado um número positivo δ, se desejarmos |f(x)
- 8| menor que ε, devemos tomar |x - 2| suficientemente
pequeno, isto é, devemos encontrar um número positivo
δ, suficientemente pequeno:
|x - 2| < δ  |f(x) - 8| < ε
2 - δ < |x| < 2 + δ  8 - ε < |f(x)| < 8 + ε

16. Epsilons (ε) e Deltas (δ)
É importante perceber que δ depende do considerado
Na tabela vê: |x-2| =0,1  |y-8| =0,2
|x - 2| < δ  |f(x) - 8| < ε
2 - δ < |x| < 2 + δ  8 - ε < |f(x)| < 8 + ε
2 – 0,1 < |x| < 2 + 0,1  8 – 0,2 < |f(x)| < 8 + 0,2
1,9 < |x| < 2,1  7,8 < |f(x)| < 8,2

17. Epsilons (ε) e Deltas (δ)
Assim:
Para qualquer valor positivo de ε podemos encontrar um
valor apropriado para δ, tal que:
a - δ < |x| < a + δ  L - ε < |f(x)| < L + ε

18. Epsilons (ε) e Deltas (δ)
Assim:

19. Epsilons (ε) e Deltas (δ)
Função f(x) definida em um intervalo I, no conceito
limite:
a - δc a + δ
L
a - δ < |x| < a + δ
L - ε < |f(x)| < L + ε

20. Propriedades dos Limites
Suponha que,
então:
2
)
(
lim
1
)
(
lim L
x
g
L
x
f a
x
a
x 
 


21. Propriedades dos Limites
O limite de uma constante é a própria constante, onde E
pertence aos números Reais:

Exemplo:
k
k
a
x 

lim 12
12
lim 4 

x
32
4
*
8
lim
*
8
lim
*
8
lim
8
lim 4
4
4
4 


 


 x
x
x x
x
x
x

22. Propriedades dos Limites
O limite do produto de n funções e o produto do limite
de n funções:
  2
*
1
)
(
lim
*
)
(
lim
)
(
*
)
(
lim L
L
x
g
x
f
x
g
x
f a
x
a
x
a
x 
 



23. Propriedades dos Limites
O limite da k-ésima potência de qualquer função é igual
a k-ésima potência do limite dessa função:
Exemplo:
    k
k
a
x
k
a
x L
x
f
x
f 1
)
(
lim
)
(
lim 
 

    27
3
lim
lim 3
3
3
3
3 

 
 x
x x
x

24. Propriedades dos Limites
O limite da soma de duas funções é a soma do limite
destas funções:
Exemplo:
  2
1
)
(
lim
)
(
lim
)
(
)
(
lim L
L
x
g
x
f
x
g
x
f a
x
a
x
a
x 



 


    9
5
2
5
lim
lim
5
lim
lim
5
lim 2
2
2
2
2
2
2
2
2 






 



 x
x
x
x
x x
x
x

25. Propriedades dos Limites
O limite da diferença duas funções é a diferença do
limite destas funções:
Exemplo:
    2
2
2
2
lim
lim
2
lim
lim
2
lim 2
2
2
2
2
2
2
2
2 






 



 x
x
x
x
x x
x
x

26. Propriedades dos Limites
O limite do quociente de duas funções é o quociente do
limite destas funções:
Exemplo:
)
0
2
(
2
1
)
(
lim
)
(
lim
)
(
)
(
lim 




 L
com
L
L
x
g
x
f
x
g
x
f
a
x
a
x
a
x
6
2
12
1
lim
3
lim
1
3
lim
3
2
3
2
3 









x
x
x
x
x
x
x

27. Propriedades dos Limites
Resumo:

28. Propriedades dos Limites
Resumo:

30. Definição intuitiva e condição
Intuitivamente, dizemos que uma função é contínua num ponto a
do seu domínio se nesse ponto ela não dá “saltos” nem apresenta
“furos”.
Dizemos que uma função f é contínua em um ponto a se as
seguintes condições estiverem satisfeitas:
1ª) f(a) está definida
2ª)
3ª)
;
)
(
lim existe
x
f
a
x
.
)
(
)
(
lim x
f
x
f
a
x



31. Exemplos
A função f é contínua
em x = a

32. Exemplos
A função g é descontínua
em x = a;
(o gráfico dá um “salto”
nesse ponto)

33. Exemplo
A função h é
descontínua em x = a
(o gráfico apresenta
um “furo” nesse
ponto)

34. Exemplo
Atende as 3
condições de
continuidade.

35. Exemplo
Não atende a 1°
condição de
continuidade.

36. Exemplo
Não atende a 2°
condição de
continuidade.

37. Exemplo
Não atende a 3°
condição de
continuidade.

38. Exemplo

40. Objetivo
Algumas das aplicações mais importantes do cálculo
diferencial são os problemas de otimização, em que
devemos encontrar a maneira ótima (melhor maneira)
de fazer alguma coisa.

41. Teorema fundamental do cálculo
Base das duas operações centrais do cálculo,
diferenciação e integração, que são considerados como
inversos um do outro. Isto significa que se uma função
contínua é primeiramente integrada e depois
diferenciada, volta-se na função original.
Ver capítulo ...

42. Derivada
Uma função F é derivável (ou diferençável) se, próximo
de cada ponto a do seu domínio, a função f(x) − f(a) se
comportar aproximadamente como uma função linear,
ou seja, se o seu gráfico for aproximadamente uma reta.
O que?!

43. Derivada
Representa a taxa de variação instantânea de uma
função:
Representa-se o declive de uma tal reta da função f no
ponto a:
)
(a
dx
dy
)
(
' a
f

44. Condição de derivação
Quadro

45. Condição de derivação
Seja uma função f: D → R, e seja D’ o conjunto de
todos os valores x tal que exista f’(x).
Chama-se função derivada de f a função f’: D’→ R tal
que:

47. Notações para a função derivada
• y’ (derivada de y)
• y’x (derivada de y em relação a x)
• Df (derivada de f)
• f’(x) (derivada de x)
• (derivada de y em relação a x)
)
(a
dx
dy

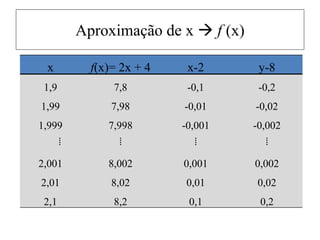
49. Teorema do Valor Médio
Existe quando:
função f seja contínua no intervalo fechado [a,b] e que f
'(x) exista no intervalo aberto a < x < b . Então, existe
pelo menos um valor c entre a e b , tal que:

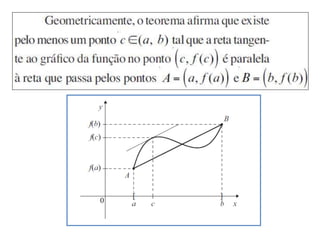
51. Teorema do Valor Médio
Existe quando:
função f seja contínua no intervalo fechado [a,b] e que f '(x)
exista no intervalo aberto a < x < b . Então, exista pelo menos um
valor c entre a e b ,
Pelos menos, professor ????
Mais o gráfico anterior apresenta apenas uma tangente
mais tem 2 pontos médios. E Ai ????

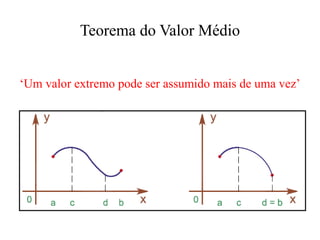
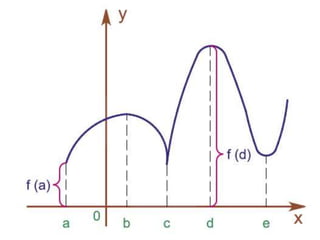
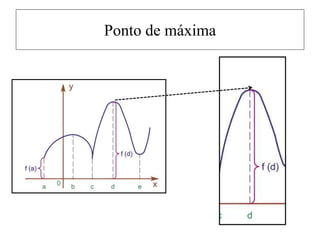
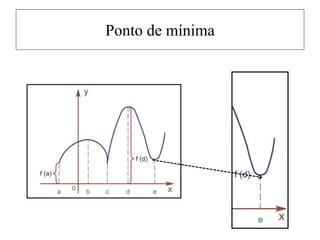
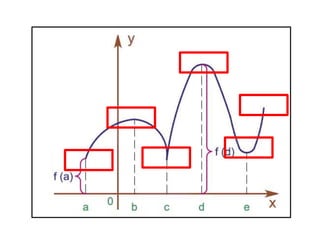
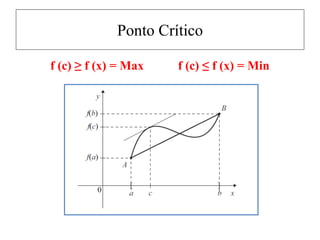
52. Teorema do Valor Médio
Se f for contínua em um intervalo fechado [a , b], então
f assume um valor máximo absoluto f (c) e um valor
mínimo absoluto f (d) em algum número c e d em [a ,
b].

53. Teorema do Valor Médio
‘Um valor extremo pode ser assumido mais de uma vez’

54. Teorema do Valor Extremo
Afirma que:
A função contínua em um intervalo fechado tem um
valor máximo e um mínimo, mas não diz como
encontrar estes valores extremos.
Vamos começar a examinar valores extremos locais!

56. Definição
Uma função f tem máximo absoluto em c se f (c) ≥ f (x)
para todo x em D, onde D é o domínio de f.
O número f (c) é chamado de valor máximo de f em D.
Analogamente, f tem um mínimo absoluto em c se f (c)
≤ f (x) para todo x em D, e o número f (c) é chamado de
valor mínimo de f em D.
Os valores máximo e mínimo de f são chamados de
valores extremos de f.

58. Ponto de máxima

59. Ponto de mínima

61. Ponto Crítico
Adota-se:
função f tem o máximo em c e o mínimo em d.
Nos pontos as retas tangentes são horizontais e
portanto cada uma tem inclinação zero.
Sabemos que a derivada é a inclinação da reta
tangente; assim f’(c) = 0 e f’(d) = 0.

62. Ponto Crítico
Então:
É qualquer ponto x no domínio de f tal que f’ (x) = 0 ou
f” (x) não exista.

63. Ponto Crítico

64. Ponto Crítico

65. Ponto Crítico

66. Ponto Crítico
f (c) ≥ f (x) = Max f (c) ≤ f (x) = Min

67. Teste Derivada da Primeira
Encontrar extremos relativos (Max e Min):
• 1º) Determine os pontos críticos de f.
• 2º) Determine o sinal de f ‘(x) à esquerda e à direita
de cada ponto crítico.

68. Entender os sinais
• Se f’(x) muda o sinal de negativo para positivo quando
nos movemos através do ponto crítico x = c, então f’(c)
é um mínimo relativo.
• Se f’(x) muda o sinal de positivo para negativo quando
nos movemos através do ponto crítico x = c, então f’(c)
é um máximo relativo.
• Se f ‘(x) não muda de sinal quando nos movemos através
do ponto crítico x =c, então f ‘(c) não é um extremo
relativo.

69. Exemplos
f (x) = x2 f’(x) = 2x
f’ (x) = 0 2x = 0
x = 0
(x): (-1) (0) (1)
F(x): (1) (0) (1)

70. Exemplos
f(x) = x3 – 3x2 -24x + 32
f’(x) = 3x2 – 6x – 24
x1= -2 e x2 = 4
f(-2) = (-2)3 – 3(-2)2 -24(-2) + 32 = 60 (máximo)
f(4) = (4)3 – 3(4)2 -24(4) + 32 = - 48 (mínimo)

71. Exercícios!!!

72. Concavidade de uma Função F
Seja uma função f diferençiavel no intervalo (a , b).
Então:
f é côncava para cima em (a , b) se f’ é crescente em
(a , b)
 f é côncava para baixo em (a , b) se f’ é decrescente
em (a , b)

73. Concavidade de uma Função F
Geometricamente, uma curva é côncava para cima se
está acima de suas retas tangentes (figura 1).
De maneira similar, uma curva é côncava para baixo se
está abaixo de suas retas tangentes (figura 2).

74. Exemplos de concavidade

75. F’’(x) para saber á concavidade
a) Se f’’(x) > 0 para cada valor de x em (a , b), então f é
côncava para cima em (a , b).
b) Se f’’(x) < 0 para cada valor de x em (a , b), então f é
côncava para baixo em (a , b).

76. F’’(x) para saber á concavidade
f(x) = x3 – 3x2 -24x + 32
f’(x) = 3x2 – 6x – 24
f’’(x) = 6x – 6
f’’(x) = 0   6x – 6 = 0
X = 1
x > 0, concavidade para cima. Mais só existe uma?

77. F’’(x) para saber á concavidade
• Concluímos que f é côncava para baixo no intervalo
(- ∞, 1) e é côncava para cima no intervalo (1, ∞).

78. Exercícios!!!
• f(x) = x4 − x2

79. Ponto de Inflexão
Um ponto no gráfico de uma função diferenciável f no
qual a concavidade muda é chamado um ponto de
inflexão.

80. Ponto de Inflexão
Um ponto (x0, f(x0)) do gráfico de uma função f é um
ponto de inflexão de f, se existe um pequeno intervalo
(a, b) ⊂ D tal que x0 ∈ (a, b) e:
1. f é côncava para cima em (a, x0) e côncava para baixo
em (x0, b), ou
2. f é côncava para baixo em (a, x0) e côncava para cima
em (x0, b).

82. Procedimento para encontrar pontos de inflexão.
1) Calcule f’’(x).
2) Determine os pontos no domínio de f para os quais
f’’(x) = 0 ou f’’(x) não existe
3) Determine o sinal de f’’(x) à esquerda e à direita de
cada ponto x = c encontrado no passo 2.
Se houver uma mudança no sinal de f’’(x) quando
passamos pelo ponto x = c, então (c , f(c)) é um ponto
de inflexão de f.

83. Exemplo
f (x) = - 0,01x3 + 1,5x2 + 200
f’(x) = -0,03x2 + 3x
f ’’ (x) = -0,06x + 3 f ’’ (x) = 0
-0,06x + 3 = 0   X = 50
• x < 50 (45) para f’’ > 0 (0,3)
• x > 50 (55) para f’’ < 0 (-0,3)

84. Exemplo
f (x) = - 0,01x3 + 1,5x2 + 200
Ponto de inflexão em X = 50
Coordenadas: (x; y)  substituir P.I. em f(x)
f (x) = y
y (P.I.: 50) = - 0,01(50)3 + 1,5(50)2 + 200
y (P.I.: 50) = 2700
Coordenadas do P.I. (x; y):(50;2700)

85. Exemplo
f (x) = - 0,01x3 + 1,5x2 + 200
(0 ≤ x ≤ 100)

86. Exercícios!!!
• f(x) = x4 − x2

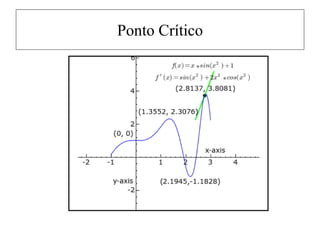
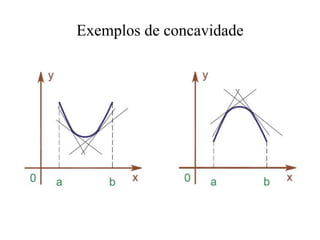
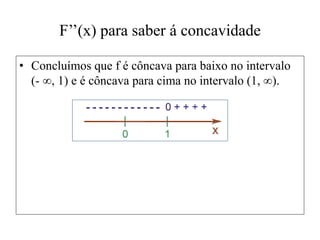
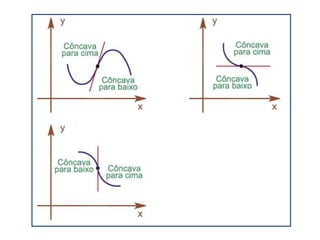
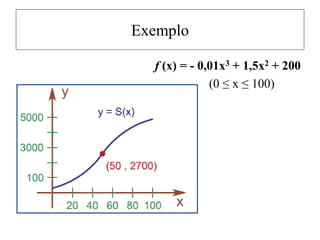
88. Fórmula de Taylor
A fórmula de Taylor é uma extensão do teorema do
valor médio
Seja f uma função tal que f e suas n primeiras derivadas
f’, f’’,..., f(n + 1) , f(n) sejam contínuas em [a,b] . Além
disso, f(n + 1)(x) existe para todo x no intervalo aberto
(a,b) .
Então, a fórmula de Taylor ou polinômio de Taylor de
ordem n , no ponto a , da função f é defina por:

89. Fórmula de Taylor
Este teorema permite aproximar uma função derivável
na vizinhança reduzida em torno de um ponto a: E (a, d)
mediante um polinômio cujos coeficientes dependem
das derivadas da função nesse ponto.

90. Exemplo
Seja f (x)=ln x , determine a fórmula ou o polinômio de
Taylor no ponto a = 1, de ordem 3:

92. Método de Newton
Newton descobriu um método para aproximar os
valores das raízes de uma equação numérica, aplicável
tanto para equações algébricas como para equações
transcendentes.
A variante desse método, hoje conhecido como Método
de Newton (Método Iterativo de Newton-Raphson), diz
o seguinte:

93. Método de Newton
"Se f (x) = 0 tem apenas uma raiz no intervalo [a, b] e se
nem f’(x) nem f’’(x) se anulam nesse intervalo,
escolhido x0 como aquele dos dois números a e b para o
qual f (x) e f’’(x) tem mesmo sinal, então:

94. Critério de convergência
Este cálculo, denominado de cálculo iterativo, é
realizado até que o critério de convergência seja
satisfeito:
ε = 1 x 10– 4

95. Dedução do método
A fórmula para o cálculo iterativo pode ser obtida
através da aproximação de uma função f(x1) em torno de
um ponto x0 por uma série de Taylor de 1° grau:

96. Dedução do método
• Se considerarmos que o valor de x = x1, está próximo
à raiz, então podemos considerar que f(x1) ≈ 0, de
modo que podemos escrever a equação na forma:

97. Exemplo
f (x) = x2 – 3
f (x) = 0   x2 – 3 = 0   x = √3
A raiz quadrada de 3 está situada entre 1 e 2.
Desta forma, tomaremos como uma aproximação inicial
x0 = 1,5.

98. Exemplo
f (x) = x2 – 3
f’(x) = 2x x0 = 1,5
x1 = 1,5 – f(1,5)/f’(1,5) = 1,75
E = |1,752 – 3| > 10– 4

99. Exemplo
 x2 = 1,75 – f(1,75)/f’(1,75) = 1,732142857
E = |1,7321428572 – 3| > 10– 4
 x3 = 1,732142857 – f(1,73)/f’(1,73) = 1,73205081
E = |1,732050812 – 3| <10– 4
Como E = |1,732050812 – 3| menor que 10– 4 paramos as iterações e tomamos
x3 como uma raiz aproximada √3, logo:
√3 = 1,73205081

100. Convergência de cálculo iterativo
E = |(ak)2 - n|
X (i + 1) Xi E
x1 1,5 1,75 -0,25
x2 1,75 1,732143 0,02
x3 1,732143 1,732051 9,2047 x 10-5