[1] O documento introduz conceitos básicos de inferência estatística, incluindo medidas de tendência central, medidas de variabilidade, distribuições de frequência e probabilidade. [2] É apresentado o software SPSS para aplicar esses conceitos em análises estatísticas de dados. [3] O documento fornece uma visão geral desses importantes conceitos estatísticos e como eles podem ser aplicados na prática usando softwares como o SPSS.

1. Inferência Estatística:
Conceitos Básicos I
Introdução, Medidas de Tendência Central, Medidas de
Variabilidade, Distribuições de Frequência e Probabilidade
Vitor Vieira Vasconcelos
Flávia da Fonseca Feitosa
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Junho de 2017

2. O Que Estudaremos na Aula de Hoje
• Populações e Amostras
• Medidas de Tendência Central: Média, Moda, Mediana
• Medidas de Variabilidade: Variância e Desvio Padrão
• Curva Normal
• Distribuições de Frequência e Probabilidade
• Escores padrão
• Cálculo da probabilidade sob a curva normal
• Prática no SPSS

3. Leitura de Referência
Capítulo 1
Tudo o que você sempre quis
saber sobre estatística
(bem, quase tudo)
(parcialmente, p. 31 – 42)

4. Como pesquisadores, estamos interessados em
investigar questões que se apliquem a toda uma
população de pessoas ou coisas
 A população pode ser geral (todos os seres
humanos) ou pequena (todos os edifícios de São
Caetano com mais de 15 andares)
 Raramente temos acesso aos dados de toda a
população, mas apenas de um subconjunto 
uma amostra, que utilizamos para inferir coisas
sobre toda a população
Populações & Amostras

5.  Quanto maior a amostra maior a probabilidade de
ela refletir a população inteira
 Amostras aleatórias da mesma população podem
fornecer resultados ligeiramente diferentes
 Em média, resultados de grandes amostras deverão
ser bastantes similares
Populações & Amostras

6. Método científico para tirar conclusões sobre os
parâmetros da população a partir da coleta,
tratamento e análise dos dados de uma amostra
recolhida dessa população
Inferência Estatística

7. Média como um modelo estatístico
Média do número de habitantes por domicílio
Nos ajuda a representar simplificadamente (modelar) este
aspecto particular da realidade
Digamos que eu tenha uma amostra de 5 domicílios, cada
qual com os seguintes números de habitantes:
Em média temos 2,6 habitantes por domicílio
1 2 3 3 4

8. Média como um modelo estatístico
Média do número de habitantes por domicílio
Em média temos 2,6 habitantes por domicílio
(considerando nossa amostra)
Mas é impossível ter 2,6 habitantes em um domicílio!!!
A média é um valor hipotético, um MODELO
criado para resumir nossos dados

9. Média como um modelo estatístico
Uma maneira útil de descrever um grupo como
um todo:
• Qual é a renda média das famílias residentes na
Mooca?
• Qual é a altura média dos edifícios em São
Caetano?
• Qual é o PIB médio dos municípios localizados
no arco do desmatamento?

10. Inferência Estatística se
resumindo a uma equação…
Saídai = (Modeloi) + erroi
Ou seja, os dados que observamos podem ser
previstos pelo modelo que escolhemos para
ajustar os dados mais um erro

11. Este modelo é preciso?
O quão diferente nossos dados reais são do
modelo criado?
Média (2,6)
Desvios
(erro do modelo)
Nr.dehabitantes
Domicílio
FIELD, A. Descobrindo a estatística
usando o SPSS. ARTMED, 2009

12. Erro total = soma dos desvios
Nr.dehabitantes
Domicílio
Zero???
Para evitar o problema do erro
direcionado (ou seja, positivo
ou negativo), elevamos cada
erro ao quadrado
Usando os desvios para estimar a
precisão do modelo
FIELD, A. Descobrindo a estatística
usando o SPSS. ARTMED, 2009

13. Usando os desvios para estimar a
precisão do modelo
Soma dos erros ao quadrado
(SS)
Nr.dehabitantes
Domicílio
Boa medida de acurácia do
nosso modelo!
Só que… quanto mais dados,
maior a SS.
FIELD, A. Descobrindo a estatística
usando o SPSS. ARTMED, 2009

14. Variância
Uma opção: Dividir SS pelo número de observações (N) 
média do quadrado do erro para a amostra
Essa medida é conhecida como VARIÂNCIA –
“média do quadrado dos desvios”
No entanto, como geralmente
queremos usar o erro na amostra para
estimar o erro na população,
dividiremos o SS pelo nr. de
observações menos 1 (graus de
liberdade).
Assim, aumentamos ligeramente a
variância amostral para produzir
estimativas não tendenciosas (mais
precisas) da variância populacional
Estimativa da variância da
população usando n amostras
aleatórias xi onde i = 1, 2, ..., n.

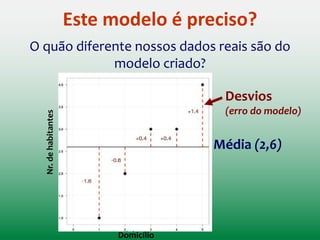
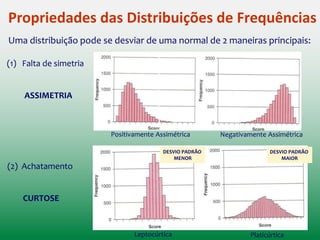
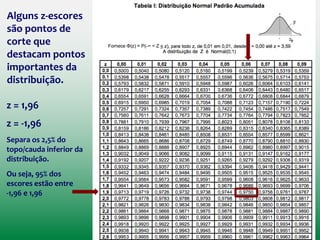
15. Um problema com o uso da variância como medida de erro: Ela é
expressa em unidades quadradas (colocamos cada erro ao
quadrado no cálculo)
No caso do exemplo, diríamos
que o quadrado da média do
erro do nosso modelo foi de
1,3 habitantes.
[Alteramos nossa unidade de medida!]
Estimativa da variância da
população usando n amostras
aleatórias xi onde i = 1, 2, ..., n.
Variância
Uma alternativa:
Tirar a raiz quadrada da variância 
DESVIO PADRÃO

16. É simplesmente a raiz quadrada da variância!
O desvio padrão (s) é uma medida de quão bem a média
representa os dados!  Média dos desvios a contar da média
Desvio Padrão
Que todos os escores são os mesmos!
Revela a dispersão dos dados em
relação à média.
s pequeno: observações estão próximas
da média
s grande: observações estão distantes da
média
s = 0 : O que significa?

17. Média com boa aderência aos dados
Médias iguais,
mas desvios padrão diferentes
Média com pobre aderência aos dados
Nr.dehabitantes
Domicílio
Nr.dehabitantes
Domicílio
Desvio Padrão = 0,5 Desvio Padrão = 1,8

19. Distribuições de Frequências
HISTOGRAMA: Gráfico com os valores observados no eixo
horizontal, com barras mostrando quantas vezes cada valor
ocorreu no conjunto de dados
Útil para avaliar as propriedades de um conjunto de valores
Moda
Escore que ocorre mais
frequentemente no
conjunto de dados
Frequência
Valores

20. Curva Normal
Maioria dos escores está em torno do centro da distribuição. A
medida que nos distanciamos do centro (média), a frequência
dos escores diminui.Frequência
Valores

23. Propriedades das Distribuições de Frequências
Uma distribuição pode se desviar de uma normal de 2 maneiras principais:
(1) Falta de simetria
ASSIMETRIA
(2) Achatamento
CURTOSE
Leptocúrtica Platicúrtica
Positivamente Assimétrica Negativamente Assimétrica
Frequência
Valores
Frequência
Valores
Frequência
Valores
Frequência
Valores
DESVIO PADRÃO
MAIOR
DESVIO PADRÃO
MENOR

24. Medidas de Tendência Central
MODA (Mo): Valor mais frequente em uma distribuição
MEDIANA (Me): Medida que separa a distribuição em duas partes iguais
MÉDIA (X): Soma de um conjunto de escores dividida pelo número total
de escores no conjunto
Medidas utilizadas para representar um conjunto de valores

25. Curva Normal
Simétrica. Média, mediana e moda coincidem!
Nem leptocúrtica, nem platicúrtica  Mesocúrtica
Do pico central, a curva cai gradualmente em ambas as extremidades,
chegando cada vez mais perto da reta básica, sem nunca tocá-la
É um modelo teórico ou ideal
que foi obtido por meio de uma
equação matemática e não de
pesquisa e coleta de dados
Entretanto, é útil para situação
reais de pesquisa pois a
distribuição de muitos
fenômenos de interesse de
pesquisa assume a forma da
curva normal
Frequência
Valores

26. Distribuições de Probabilidade
Distribuições de frequência podem ser usadas para obter uma
ideia aproximada da probabilidade de um escore ocorrer
(ou intervalo)
Exemplo da Aula Anterior: Considerando que a distribuição do
número de residentes por domicílio possui a forma de uma
distribuição normal, qual seria a probabilidade de termos, nos
dados, um domicílio com 4 habitantes ou menos?
PROBABILIDADE: NOÇÃO IMPORTANTE PARA A
TOMADA DE DECISÃO!!!

27. Distribuições de Probabilidade
Distribuições de frequência podem ser usadas para obter uma
ideia aproximada da probabilidade de um escore ocorrer
(ou intervalo)
Exemplo da Aula Anterior: Considerando que a distribuição do
número de residentes por domicílio possui a forma de uma
distribuição normal, qual seria a probabilidade de termos, nos
dados, um domicílio com 4 habitantes ou menos?
 Para facilitar nosso trabalho, estatísticos elaboraram uma
forma matemática que especifica versões idealizadas das
distribuições: DISTRIBUIÇÕES DE PROBABILIDADE

28. Distribuições de Probabilidade
A distribuição de probabilidades associa uma
probabilidade a cada resultado numérico de um
experimento, ou seja, dá a probabilidade de cada
valor (ou de intervalo de valores) de uma variável
aleatória.
 É análoga a uma distribuição de frequência, exceto por ser
baseada em teoria ao invés de dados empíricos
(observações do mundo real)
 As probabilidades representam a chance de cada escore
ocorrer, diretamente análoga às porcentagens em uma
distribuição de frequência.

29. A curva normal como uma
distribuição de probabilidade
 A curva normal é um ideal teórico
 No entanto, existem muitas distribuições de dados reais que
se aproximam da forma da curva normal
É sempre importante checar!!!!
Construir um histograma é um bom começo!
Algumas variáveis nas ciências sociais, não se enquadram
(renda e distribuição etária, por exemplo)

30. A curva normal como uma
distribuição de probabilidade

31. A curva normal como uma
distribuição de probabilidade
Exemplo Aula Anterior:
Residentes por Domicílio
Média = 2,6; s = 1,14
1,46 3,742,6

32. Voltando a nossa pergunta:
Considerando que a distribuição do número de residentes por
domicílio possui a forma de uma distribuição normal, qual seria a
probabilidade de termos, nos dados, um domicílio com 4
habitantes ou menos?
1,46 3,742,6
4
Residentes por Domicílio
Média = 2,6; s = 1,14

33. Distribuição Normal Padrão
 Já calcularam a probabilidade de certos escores ocorrerem
numa distribuição normal com Média = 0 & Desvio padrão = 1
DISTRIBUIÇÃO NORMAL PADRÃO

34. Distribuição Normal Padrão
MAS… a distribuição dos meus dados não apresenta
média = zero e desvio padrão = 1!
E aí????
QUALQUER CONJUNTO DE DADOS PODE SER
CONVERTIDO EM UM CONJUNTO QUE TENHA MÉDIA
ZERO E DESVIO PADRÃO 1 !
OBA!!!!
Como fazer:
(1) Para centrar dados em zero, pegamos cada escore e
subtraímos dele a média de todos os escores.
(2) Dividimos o escore resultante pelo desvio padrão
para assegurar os os resultados terão DP = 1
escores-z

35. Distribuição Normal Padrão
Voltando a nossa pergunta:
Considerando que a distribuição do número de residentes por
domicílio possui a forma de uma distribuição normal, qual seria a
probabilidade de termos, nos dados, um domicílio com 4
habitantes ou menos?
Considerando que a distribuição dos dados possa ser descrita como uma
distribuição normal, com média = 2,6 e desvio padrão = 1,14
escores-z
Primeiro Passo: Converter o valor 4 em
um escore-z  (4 - 2,6)/1,14 = 1,23

36. Distribuição Normal Padrão
1,23

37. Distribuição Normal Padrão
Voltando a nossa pergunta:
Considerando que a distribuição do número de residentes por
domicílio possui a forma de uma distribuição normal, qual seria a
probabilidade de termos, nos dados, um domicílio com 4
habitantes ou menos?
Considerando que a distribuição dos dados possa ser descrita como uma
distribuição normal, com média = 2,6 e desvio padrão = 1,14
escores-z
Primeiro Passo: Converter o valor 4 em
um escore-z  (4 - 2,6)/1,14 = 1,23
Segundo Passo: Verificar tabela

38. z = 1,23
A probabilidade
de termos um
domicílio com
até 4 habitantes
é de 0,8907
(89,07%)
Complementarmente,
a probabilidade de
termos um domicílio
com mais de 4
habitantes é de 0,1093
(10,93%)

39. z = 1,96
z = -1,96
Separa os 2,5% do
topo/cauda inferior da
distribuição.
Ou seja, 95% dos
escores estão entre
-1,96 e 1,96
Alguns z-escores
são pontos de
corte que
destacam pontos
importantes da
distribuição.

40. z = 1,96
z = -1,96
Separa os 2,5% do
topo/cauda inferior da
distribuição.
Ou seja, 95% dos
escores estão entre
-1,96 e 1,96
Alguns z-escores
são pontos de
corte que
destacam pontos
importantes da
distribuição.
1,96-1,96

41. z = -2,58
z = +2,58
99% dos escores estão
entre -2,58 e 2,58
z = -3,29
z = +3,29
99,9% dos escores estão
entre -3,29 e 3,29
Alguns z-escores
são pontos de
corte que
destacam pontos
importantes da
distribuição.

43. Prática
O Ambiente SPSS