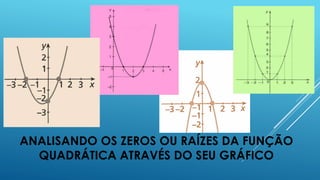
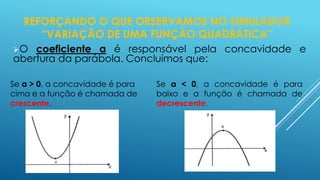
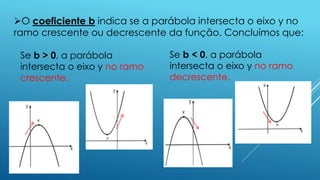
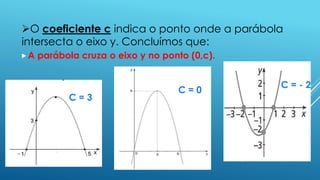
O documento apresenta os conceitos fundamentais sobre funções quadráticas, incluindo: (1) como identificar os coeficientes a, b e c; (2) como determinar os zeros ou raízes; (3) como determinar o vértice. Exemplos são fornecidos para ilustrar cada conceito.

1. Elaborado por:
Prof.ª Adriana de Araújo

2. CARACTERÍSTICAS

3. MAS NEM SEMPRE NOSSA EXPRESSÃO ALGÉBRICA
APARECERÁ ASSIM... VAMOS VERIFICAR EM OUTRAS
FORMAS SE VOCÊ CONSEGUE IDENTIFICAR OS VALORES
DOS COEFICIENTES a, b E c NAS FUNÇÕES
QUADRÁTICAS A SEGUIR.
f(x) = (x – 3)²
f(x) = ( x +2 )( x – 2 )
f(x) = 3x(x -1)

4. E AÍ CONSEGUIRAM? VAMOS VERIFICAR!

Com certeza quem se recordou de fatoração e produtos notáveis
conseguiu identificar os coeficientes. Vamos relembrar!
 f(x)
= (x + 3)² → é um quadrado da soma → (quadrado do 1º)+ (duas
vezes o 1º pelo 2º) + (quadrado do 2º), logo teremos:
f(x) = x² + 2. x. 3 + 3²
f(x) = x² + 6x + 9
onde
a = 1, b = 6 e c = 9
 f(x)
= (x +2)(x – 2) → é um produto da soma pela diferença → (quadrado
do 1º) – ( quadrado do 2º), logo teremos:
f(x) = x² + 2²
f(x) = x² + 4
onde a = 1 , b = 0 e c = 4
 f(x)
= 3x (x -1) → é uma multiplicação de monômio por polinômio →
multiplicamos o termo(monômio) de fora do parênteses pelas parcelas
de dentro(polinômio) e somamos os resultados, logo teremos:
f(x) = 3x. X + 3x .(-1)
f(x) = 3x² - 3x
onde a = 3, b = 3 e c = 0

5. REPRESENTAÇÃO ALGÉBRICA
f(x)
= ax² + bx + c
REPRESENTAÇÃO GRÁFICA
 é uma curva aberta
chamada parábola.
Uma Pará...o quê? Calma, para
entender melhor vamos assistir um
vídeo!

6. APRENDENDO MAIS SOBRE PARÁBOLAS!
ou acesse http://www.youtube.com/watch?v=yc164_2VvpI

7. ZEROS OU RAÍZES DE UMA
FUNÇÃO QUADRÁTICA
Os
zeros ou raízes da função
quadrática f(x) = ax² + bx =c são as
raízes da equação do 2º grau ax² +
bx + c = 0, ou seja, temos que
resolver a equação.

8. PODEMOS RESOLVER POR FATORAÇÃO
Exemplo:
f(x) = x² - 4, a equação correspondente é x² - 4 = 0, fatorando o
1º membro da equação temos:
x² - 4 = 0 → (x - 2)(x + 2) = 0 para que o produto seja zero, pelo
menos um dos fatores precisa ser zero. Logo, (x – 2) = 0 ou (x +
2) = 0
Se x – 2 = 0, então x = 2
Se x + 2 = 0, então x = - 2
Assim os zeros da função são – 2 e 2. verificando, teremos :
f(x) = x² - 4
→ (- 2)² - 4 = 4 – 4 = 0 e 2² - 4 = 4 – 4 = 0

9. OUTRO EXEMPLO:
f(x) = x² - 6x + 9, a equação correspondente é x² - 6x + 9 = 0,
fatorando o 1º membro da equação temos:
x² - 6x + 9 = 0 → (x - 3)² = 0 → (x - 3)(x – 3) = 0 para que o
produto seja zero, pelo menos um dos fatores precisa ser
zero. Logo, ( x – 3) = 0 ou (x - 3) = 0
Se x – 3 = 0, então x = 3
Se x - 3 = 0, então x = 3
Assim as raízes da função são iguais (dupla) = 3. verificando,
teremos :
f(x) = x² - 6x + 9 → 3² - 6.3 + 9 = 9 - 18 + 9 = - 9 + 9 = 0

10. PODEMOS RESOLVER PELA FÓRMULA DE
BÁSKARA
f(x) = x² - 7x + 6, fazemos:
f(x) = 0 → x² - 7x + 6 = 0 (equação do 2º grau)
Resolvendo: a = 1 , b = -7 e c = 6
𝒙=
𝑥
−𝒃±
𝒃 𝟐 −𝟒𝒂𝒄
𝟐𝒂
7± 49−24
=
2
7+5
12
′
𝑥 =
=
2
2
𝑥=
𝑥=
=6
− −7 ±
7±√25
2
"
𝑥 =
−7 2 −4.1.6
2.1
𝑥=
7−5
2
2
2
7±5
2
= =1
AS RAÍZES DA FUNÇÃO SÃO 1 E 6.

11. CONCLUINDO:
AS RAÍZES OU ZEROS DA FUNÇÃO:
ALGEBRICAMENTE – são os valores de x
tais que f(x) ou y seja zero.
GEOMETRICAMENTE – são os pontos
(abscissas) em que a parábola intercepta
o eixo x.

12. VAMOS REFORÇAR O QUE APRENDEMOS COM O
VÍDEO
ou acesse http://www.youtube.com/watch?v=uAiBrgiig-c

13. ANALISANDO OS ZEROS OU RAÍZES DA FUNÇÃO
QUADRÁTICA ATRAVÉS DO SEU GRÁFICO

14. IMPORTANTE !!!
A PARÁBOLA PODE INTERSECTAR O EIXO x EM UM, DOIS OU
NENHUM PONTO, DEPENDE DO VALOR DE ∆ = b² - 4ac DA
EQUAÇÃO CORRESPONDENTE. CONCLUÍMOS QUE:
∆ = 0 ,uma raiz real ∆ > 0, duas raízes reais ∆ < 0, nenhuma raiz
dupla (a parábola
diferentes (a parábola real (a parábola não
intersecta o eixo x
intersecta o eixo x em intersecta o eixo).
em um só ponto).
dois pontos).

15. AGORA VAMOS PRATICAR UM POUCO!
Determine, se existirem, os zeros das funções quadráticas
usando a fórmula:
a) F(x)=
x² - 3x
b) F(x)
= x² + 4x + 5
c) F(x)
= - x² + 2x + 8
d) F(x)
= x² + 10x + 25
(Extraídos do Livro Matemática Contextos e Aplicações, do autor Dante, Volume 1 Ensino
Médio, pág.162)

16. Estudando o efeito dos coeficientes a, b e c na
parábola que representa a função
f(x) = ax² + bx + c.
Para isso vamos utilizar a ajuda de um software
chamado VARIAÇÃO DA FUNÇÃO QUADRÁTICA,
acessando o endereço:
http://www.cdme.im.-uff.mat.br/quadratica/quadratica-html/QP1.html

17. REFORÇANDO O QUE OBSERVAMOS NO SIMULADOR
“VARIAÇÃO DE UMA FUNÇÃO QUADRÁTICA”
O
coeficiente a é responsável pela concavidade e
abertura da parábola. Concluímos que:
Se a > 0, a concavidade é para
cima e a função é chamada de
crescente.
Se a < 0, a concavidade é para
baixo e a função é chamada de
decrescente.

18. O coeficiente b indica se a parábola intersecta o eixo y no
ramo crescente ou decrescente da função. Concluímos que:
Se b > 0, a parábola
intersecta o eixo y no ramo
crescente.
Se b < 0, a parábola
intersecta o eixo y no ramo
decrescente.

19. O coeficiente c indica o ponto onde a parábola
intersecta o eixo y. Concluímos que:
A
parábola cruza o eixo y no ponto (0,c).
C=3
C=3
C=0
C=-2

20. AGORA VAMOS ESTUDAR MAIS UM PONTO
MUITO IMPORTANTE NO GRÁFICO DE UMA
FUNÇÃO QUADRÁTICA
Sabe que ponto é este? É o vértice da
parábola...isso mesmo o vértice é o ponto em
que a parábola faz a curva, ou seja, o ponto em
que a curva muda de direção.
O vértice permite determinar a Imagem da
função e também seu valor máximo ou mínimo.

21. DETERMINANDO O VÉRTICE DA PARÁBOLA
A
parábola é simétrica em relação ao eixo vertical, logo o valor do x do
vértice será a média aritmética entre os valores das raízes da função.
Exemplo:
Dada a função f(x) = x² - 7x + 6 , temos como raízes x’ = 1 e x” = 6
Xv = x’ + x” = 1 + 6 = 7 = 3,5 logo substituindo x = 3,5 na função teremos,
2
2
2
f(3,5) = 3,5² - 7 . 3,5 + 6 = 12,25 – 24,5 + 6 = - 6,25, esse é o valor do yv .
Conclusões: o vértice desta parábola é o ponto (3,5; -6,25);
O valor mínimo desta função é : - 6,25;
A imagem é definida por : Im = { y є IR/y > - 6,25 }

22. A
outra forma de determinar as coordenadas do
vértice da parábola é aplicando as fórmulas:
Xv = - b
e
yv = - ∆
2a
4a
Dada a mesma função anterior f(x) = x² - 7x + 6, teremos
utilizando as fórmulas:
Xv = - b = - ( - 7) = 3,5
2a
2.1
e
yv = - ∆ = - 25 = - 6,25
4a
4.1
VIRAM COMO ENCONTRAMOS OS MESMOS VALORES!

23. REFORÇAMOS QUE:
SE A CONCAVIDADE DA PARÁBOLA É PARA
CIMA ( a > 0), O yv SERÁ VALOR MÍNIMO DA
FUNÇÃO E Im = { y є IR/ y > yv}
SE A CONCAVIDADE DA PARÁBOLA É PARA
BAIXO (a < 0), O yv SERÁ O VALOR MÁXIMO
DA FUNÇÃO E Im = { y є IR/ y < yv}

24. EXERCITANDO UM POUCO:
1. Determine o ponto V(xv, yv), vértice da parábola que
representa o gráfico das seguintes funções:
a)
y = x² - 6x + 5
b)
y = 3x² - 4x
c)
y = x² - 4
d)
y = - 6x²
e)
y = - x² + x – 3
Exercícios extraídos do Livro: Matemática Fundamental – Uma Nova Abordagem, de
Giovanni, Bonjorno e Giovanni Jr.
Pág. 133

25. AGORA CHEGAMOS NA MELHOR HORA...

26. PARA CONHECER ALGUMAS APLICAÇÕES
VAMOS ASSISTIR AO VÍDEO
OU ACESSE http://m3.ime.unicamp.br/recursos/1160

27. VAMOS VER ALGUMAS APLICAÇÕES EM FÍSICA
Voltando e acessando o endereço abaixo que
é do Software de “Variação de uma Função
Quadrática”, teremos algumas atividades com
velocidade...
http://www.cdme.im.-uff.mat.br/quadratica/quadratica-html/QP1.html

28. OUTRAS APLICAÇÕES:
1.
Em nossa Escola será construída uma quadra poliesportiva, a área
disponível para esta construção é de 375m². Sabe-se que o
comprimento da quadra excede a largura em 10 unidades.Qual
será as dimensões desta quadra?
Plano de solução – vamos desenhar para entendermos melhor , vejamos:
largura = x
comprimento = x + 10
Essa medida que não conhecemos o valor será a nossa incógnita que chamaremos
de x. Devemos encontrar o valor de x. Sabemos que trata-se de uma quadra
retangular, pois os lados são diferentes, sabemos também que a área do retângulo
é dado por base x altura, ou comprimento x largura, logo teremos:
A = x (x + 10)
A = x. x + x .10
A = X² + 10 X
agora é só resolver a equação!

29. 2. Um diagramador está definindo as dimensões que terá uma revista. Necessita
que o comprimento de cada página seja igual à largura e que a superfície da
cada página seja de 324cm². Quais as medidas que cumprem as duas
condições?
3. O lucro, em reais, de uma empresa na venda de determinado produto é dado
pela função l(x) = – 2x2 + 300x – 16, onde l(x) é o lucro e x representa a quantidade
de produtos vendidos.Determine o lucro máximo obtido pela empresa na venda
desse produto.
4. Uma bola, ao ser chutada num tiro de meta por um goleiro, numa partida de
futebol, teve sua trajetória descrita pela equação h(t) = -2t² + 8t, onde t é o tempo
medido em segundos e h(t) é a altura em metros da bola no instante t. Determine:
a. O instante em que a bola retornará ao solo.
b. A altura máxima atingida pela bola.