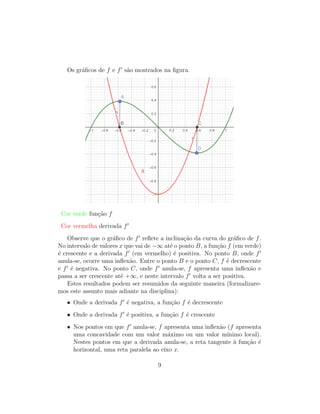
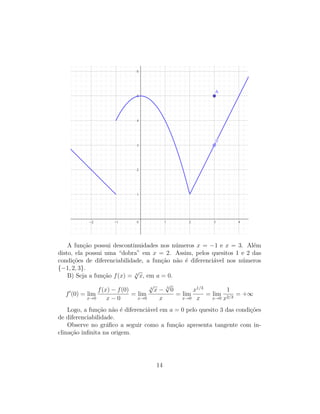
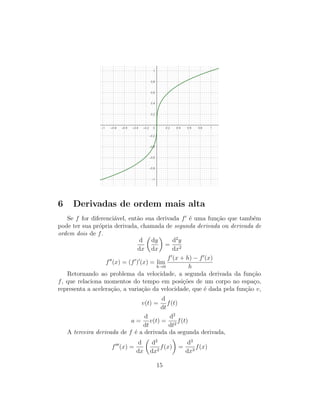
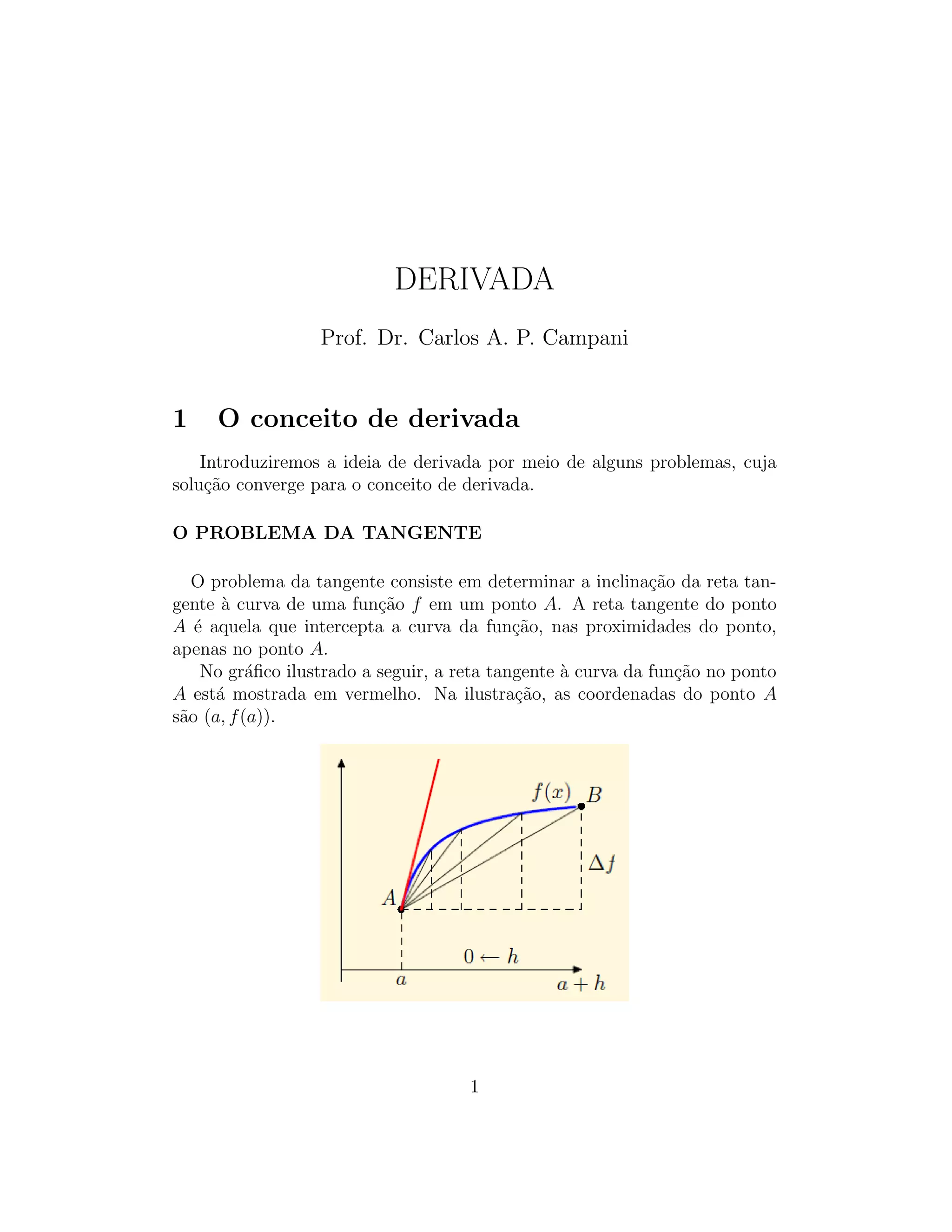
O documento introduz o conceito de derivada através de problemas como a tangente e a velocidade. A derivada de uma função f em um ponto a é definida como o limite da taxa de variação de f quando h tende a zero. A derivada representa a inclinação da reta tangente e pode ser usada para calcular taxas de variação instantâneas.

1. DERIVADA
Prof. Dr. Carlos A. P. Campani
1 O conceito de derivada
Introduziremos a ideia de derivada por meio de alguns problemas, cuja
solu¸c˜ao converge para o conceito de derivada.
O PROBLEMA DA TANGENTE
O problema da tangente consiste em determinar a inclina¸c˜ao da reta tan-
gente `a curva de uma fun¸c˜ao f em um ponto A. A reta tangente do ponto
A ´e aquela que intercepta a curva da fun¸c˜ao, nas proximidades do ponto,
apenas no ponto A.
No gr´afico ilustrado a seguir, a reta tangente `a curva da fun¸c˜ao no ponto
A est´a mostrada em vermelho. Na ilustra¸c˜ao, as coordenadas do ponto A
s˜ao (a, f(a)).
1

2. Podemos tomar um ponto B, diferente do ponto A, sobre a curva da
fun¸c˜ao, de coordenadas (x, f(x)) ou (a + h, f(a + h)), tomando x = a + h.
Os pontos A e B formam um triˆangulo retˆangulo cujo cateto oposto ´e ∆f =
f(x) − f(a) e o cateto adjacente ´e x − a ou h.
A inclina¸c˜ao do segmento de reta AB ´e dada por
mAB =
∆f
x − a
=
f(x) − f(a)
x − a
=
f(a + h) − f(a)
h
Observe que ao tomar o ponto B cada vez mais pr´oximo do ponto A, o
segmento de reta AB aproxima-se da inclina¸c˜ao da reta tangente do ponto
A, ou seja,
m = lim
B→A
mAB
e m ´e a inclina¸c˜ao da reta tangente.
Quando B → A temos x → a ou h → 0. Assim, podemos obter as duas
formula¸c˜oes da inclina¸c˜ao da reta tangente:
m = lim
x→a
f(x) − f(a)
x − a
ou
m = lim
h→0
f(a + h) − f(a)
h
desde que estes limites existam.
Assim, a equa¸c˜ao da reta tangente ao ponto (a, f(a)) ´e dada por
y − f(a) = m(x − a) ou y = m(x − a) + f(a)
EXEMPLO
Seja f(x) = 3
x
. Queremos determinar a inclina¸c˜ao da reta tangente e a
equa¸c˜ao da reta tangente que passa pelo ponto (3, 1). Ent˜ao,
m = lim
h→0
f(3 + h) − f(3)
h
= lim
h→0
3
3+h
− 1
h
= lim
h→0
3−3−h
3+h
h
= lim
h→0
−h
(3 + h)h
=
lim
h→0
−1
3 + h
= −
1
3
2

3. e a equa¸c˜ao da reta tangente `a fun¸c˜ao no ponto (3, 1) fica
y − 1 = −
1
3
(x − 3)
y = −
x
3
+ 2
O gr´afico da fun¸c˜ao e da reta tangente ´e mostrado na figura a seguir.
Observe que a inclina¸c˜ao ´e negativa, portanto a reta tangente indica que
a fun¸c˜ao ´e decrescente neste ponto.
O PROBLEMA DA VELOCIDADE
Imaginemos um ve´ıculo movimentando-se em uma via reta, assumindo
diferentes velocidades ao longo do trajeto.
3

4. Vamos supor que existe uma fun¸c˜ao f que determina, para cada instante
no tempo (por exemplo, em segundos), a posi¸c˜ao do ve´ıculo na via (por
exemplo, em metros),
y = f(t)
onde t ´e o tempo em segundos e y ´e a posi¸c˜ao na via em metros.
Sabemos que a velocidade m´edia de um corpo ´e dada pela raz˜ao entre o
deslocamento no espa¸co e o tempo transcorrido:
velocidade m´edia =
deslocamento no espa¸co
tempo transcorrido
Consideremos o deslocamento ocorrido entre os instantes de tempo t1 e
t2. Neste caso, a velocidade m´edia neste segmento do trajeto ´e
velocidade m´edia =
f(t2) − f(t1)
t2 − t1
Assumindo t2 = t1 + ∆t,
velocidade m´edia =
f(t1 + ∆t) − f(t1)
∆t
Mas esta velocidade ´e uma velocidade m´edia em um determinado seg-
mento do trajeto. Estamos interessados na velocidade instantˆanea v em um
determinado momento t1 do tempo. Isso pode ser obtido quando tomamos o
limite de t2 → t1 ou ∆t → 0,
v(t1) = lim
∆t→0
f(t1 + ∆t) − f(t1)
∆t
que ´e a inclina¸c˜ao da reta tangente `a curva da fun¸c˜ao f no instante t1.
EXEMPLO
Suponha uma bola abandonada no alto de uma torre de 300m de altura.
Qual sua velocidade ap´os 5s?
y = f(t) = 4, 9t2
v(5) = lim
h→0
f(5 + h) − f(5)
h
= lim
h→0
4, 9(5 + h)2
− 4, 9.52
h
=
lim
h→0
4, 9(52
+ 10h + h2
− 52
)
h
= lim
h→0
4, 9h(10 + h)
h
=
lim
h→0
[4, 9(10 + h)] = 4, 9.10 = 49 m/s
4

5. TAXAS DE VARIAC¸ ˜AO
Suponha uma quantidade que varie dependendo de outra quantidade. E-
xemplos disso s˜ao in´umeros:
• Pensemos na economia. Ent˜ao, d´ıvida p´ublica, desemprego, infla¸c˜ao,
PIB, s˜ao parˆametros que dependem uns dos outros.
• Uma popula¸c˜ao de bact´erias em um habitat, com rela¸c˜ao `a tempera-
tura. Espera-se que quanto maior a temperatura, maior a popula¸c˜ao
de bact´erias.
• Ocorrˆencia de doen¸cas endˆemicas, com rela¸c˜ao `a renda m´edia da po-
pula¸c˜ao que vive em uma determinada regi˜ao. Havendo aumento da
renda m´edia, h´a redu¸c˜ao na ocorrˆencia destas doen¸cas endˆemicas na
popula¸c˜ao.
Assumimos que temos uma fun¸c˜ao f que relaciona as duas quantidades
x e y, y = f(x). Consideremos os incrementos (ou varia¸c˜oes) de x e y:
∆x = x2 − x1
e
∆y = y2 − y1 = f(x2) − f(x1)
Entender o quanto uma quantidade varia em rela¸c˜ao `a varia¸c˜ao de outra
quantidade pode ser muito importante. Podemos definir a varia¸c˜ao m´edia de
y em rela¸c˜ao a x:
∆y
∆x
=
f(x2) − f(x1)
x2 − x1
Queremos determinar a taxa de varia¸c˜ao instantˆanea de y em rela¸c˜ao a
x, que ´e a inclina¸c˜ao da reta tangente da curva da fun¸c˜ao f:
taxa instantˆanea = lim
∆x→0
∆y
∆x
= lim
x2→x1
f(x2) − f(x1)
x2 − x1
5

6. 2 Defini¸c˜ao de derivada
A solu¸c˜ao dos problemas apresentados na se¸c˜ao anterior converge para o
conceito de derivada.
A derivada de uma fun¸c˜ao f em um n´umero a, denotada por f (a), ´e
definida como:
f (a) = lim
h→0
f(a + h) − f(a)
h
ou
f (a) = lim
x→a
f(x) − f(a)
x − a
desde que o limite exista.
EXEMPLOS
A) Encontre a derivada da fun¸c˜ao f(x) = x2
− 8x + 9 no n´umero a = 5.
Obtenha a equa¸c˜ao da reta tangente `a fun¸c˜ao f no mesmo ponto a.
f (a) = lim
h→0
f(a + h) − f(a)
h
= lim
h→0
(a + h)2
− 8(a + h) + 9 − a2
+ 8a − 9
h
=
lim
h→0
a2
+ 2ah + h2
− 8a − 8h + 9 − a2
+ 8a − 9
h
= lim
h→0
h2
+ 2ah − 8h
h
=
lim
h→0
(h + 2a − 8) = 2a − 8
Ent˜ao, f (5) = 2.5 − 8 = 2.
A equa¸c˜ao da reta tangente ao ponto a = 5 ´e dada por:
y − f(a) = f (a)(x − a)
f(5) = −6
y − (−6) = 2(x − 5)
y = 2x − 16
6

7. B) Determine a derivada da fun¸c˜ao g(x) =
√
x no n´umero a = 4. Deter-
mine tamb´em a equa¸c˜ao da reta tangente a este ponto.
g (a) = lim
h→0
√
a + h −
√
a
h
= lim
h→0
√
a + h −
√
a
h
√
a + h +
√
a
√
a + h +
√
a
=
lim
h→0
a + h − a
h(
√
a + h +
√
a)
= lim
h→0
1
√
a + h +
√
a
=
1
2
√
a
Ent˜ao g (4) = 1/4
A equa¸c˜ao da reta tangente `a curva da fun¸c˜ao g no ponto a = 4 ´e:
y − g(a) = g (a)(x − a)
y − 2 =
1
4
(x − 4)
y =
x
4
+ 1
C) Seja f(x) = x−1
x+1
. Determine a derivada da fun¸c˜ao em a = 2. Apresente
tamb´em a equa¸c˜ao da reta tangente a este ponto.
f (a) = lim
h→0
f(a + h) − f(a)
h
= lim
h→0
a+h−1
a+h+1
− a−1
a+1
h
=
lim
h→0
(a+1)(a+h−1)−(a+h+1)(a−1))
(a+h+1)(a+1)
h
=
lim
h→0
a2
+ ah − a + a + h − 1 − (a2
− a + ah − h + a − 1)
(a + h + 1)(a + 1)h
=
lim
h→0
a2
+ ah + h − 1 − a2
− ah + h + 1
(a + h + 1)(a + 1)h
= lim
h→0
2h
(a + h + 1)(a + 1)h
=
lim
h→0
2
(a + h + 1)(a + 1)
=
2
(a + 1)2
=
2
(2 + 1)2
=
2
32
=
2
9
Como f(2) = 2−1
2+1
= 1
3
, a reta tangente ao ponto (2, 1/3) ´e
y −
1
3
=
2
9
(x − 2)
y =
2
9
x −
1
9
7

8. D) Determine a derivada de f(x) = 1
x+1
em a = 3, usando a seguinte
formula¸c˜ao para o c´alculo de derivadas:
f (a) = lim
x→a
f(x) − f(a)
x − a
f (a) = lim
x→a
1
x+1
− 1
a+1
x − a
= lim
x→a
a+1−(x+1)
(x+1)(a+1)
x − a
= lim
x→a
a − x
(x + 1)(a + 1)(x − a)
=
lim
x→a
−
x − a
(x + 1)(a + 1)(x − a)
= lim
x→a
−
1
(x + 1)(a + 1)
= −
1
(a + 1)2
=
−
1
(3 + 1)2
= −
1
16
3 A derivada como uma fun¸c˜ao
Podemos mudar nosso ponto de vista e considerar, n˜ao a derivada em um
n´umero a, mas a derivada como uma fun¸c˜ao:
f (x) = lim
h→0
f(x + h) − f(x)
h
f ´e denominada de derivada de f.
EXEMPLOS
A) Seja a fun¸c˜ao f(x) = x3
− x. Determine f e compare os gr´aficos de f
e f .
f (x) = lim
h→0
f(x + h) − f(x)
h
= lim
h→0
(x + h)3
− (x + h) − x3
+ x
h
=
lim
h→0
x3
+ 3hx2
+ 3h2
x + h3
− x − h − x3
+ x
h
=
lim
h→0
3hx2
+ 3h2
x + h3
− h
h
= lim
h→0
(3x2
+ 3hx + h2
− 1) = 3x2
− 1
8

9. Os gr´aficos de f e f s˜ao mostrados na figura.
Cor verde fun¸c˜ao f
Cor vermelha derivada f
Observe que o gr´afico de f reflete a inclina¸c˜ao da curva do gr´afico de f.
No intervalo de valores x que vai de −∞ at´e o ponto B, a fun¸c˜ao f (em verde)
´e crescente e a derivada f (em vermelho) ´e positiva. No ponto B, onde f
anula-se, ocorre uma inflex˜ao. Entre o ponto B e o ponto C, f ´e decrescente
e f ´e negativa. No ponto C, onde f anula-se, f apresenta uma inflex˜ao e
passa a ser crescente at´e +∞, e neste intervalo f volta a ser positiva.
Estes resultados podem ser resumidos da seguinte maneira (formalizare-
mos este assunto mais adiante na disciplina):
• Onde a derivada f ´e negativa, a fun¸c˜ao f ´e decrescente
• Onde a derivada f ´e positiva, a fun¸c˜ao f ´e crescente
• Nos pontos em que f anula-se, f apresenta uma inflex˜ao (f apresenta
uma concavidade com um valor m´aximo ou um valor m´ınimo local).
Nestes pontos em que a derivada anula-se, a reta tangente `a fun¸c˜ao ´e
horizontal, uma reta paralela ao eixo x.
9

10. B) Determine a derivada de g(x) = 1√
x
.
g (x) = lim
h→0
g(x + h) − g(x)
h
= lim
h→0
1√
x+h
− 1√
x
h
= lim
h→0
√
x−
√
x+h
√
x+h
√
x
h
=
lim
h→0
√
x −
√
x + h
h
√
x + h
√
x
√
x +
√
x + h
√
x +
√
x + h
=
lim
h→0
x − (x + h)
h
√
x + h
√
x(
√
x +
√
x + h)
=
lim
h→0
−h
h
√
x + h
√
x(
√
x +
√
x + h)
=
lim
h→0
−
1
√
x + h
√
x(
√
x +
√
x + h)
= −
1
2x
√
x
C) Determine a derivada de f(x) = x +
√
x.
f (x) = lim
h→0
x + h +
√
x + h − (x +
√
x)
h
= lim
h→0
h +
√
x + h −
√
x
h
=
lim
h→0
1 +
√
x + h −
√
x
h
= 1 + lim
h→0
√
x + h −
√
x
h
=
1 + lim
h→0
√
x + h −
√
x
h
√
x + h +
√
x
√
x + h +
√
x
=
1 + lim
h→0
x + h − x
h(
√
x + h +
√
x)
= 1 + lim
h→0
h
h(
√
x + h +
√
x)
=
1 + lim
h→0
1
√
x + h +
√
x
= 1 +
1
2
√
x
10

11. 4 Nota¸c˜ao usada para representar derivadas
Seja y = f(x) uma fun¸c˜ao. Ent˜ao s˜ao nota¸c˜oes v´alidas para representar
a derivada de f:
1. y
2. f (x)
3. dy
dx
4. d
dx
f(x)
5. Df(x)
6. Dxf(x)
A derivada pode ser entendida como uma opera¸c˜ao que transforma uma
fun¸c˜ao em outra. Esta opera¸c˜ao ´e chamada de diferencia¸c˜ao e o c´alculo
toma o nome de c´alculo diferencial. D e d
dx
s˜ao chamados de operadores
diferenciais.
H´a uma grande vantagem nos operadores que tornam expl´ıcita a vari´avel
em rela¸c˜ao `a qual ser´a feita a opera¸c˜ao, como d
dx
e Dx, e isso fica evidente
em fun¸c˜oes com mais de uma vari´avel.
A nota¸c˜ao dy
dx
´e muito interessante e proveitosa quando usamos derivadas
para expressar taxas de varia¸c˜ao, basta ver que:
dy
dx
= lim
∆x→0
∆y
∆x
mas n˜ao devemos ser tentados a imaginar o operador d/dx como uma raz˜ao
ou fra¸c˜ao. ∆y/∆x ´e uma fra¸c˜ao de duas varia¸c˜oes, mas d/dx ´e um operador
diferencial.
5 Condi¸c˜ao para uma fun¸c˜ao ser diferenci´avel
Uma fun¸c˜ao f ´e diferenci´avel ou deriv´avel em a se f (a) existir. Uma
fun¸c˜ao f ´e diferenci´avel em um intervalo aberto (u, v) se for diferenci´avel em
cada ponto deste intervalo. Essa defini¸c˜ao tamb´em vale para os intervalos
(u, +∞), (−∞, u) e (−∞, +∞) = R.
Como um exemplo, vamos analisar a fun¸c˜ao f(x) = |x|.
Lembremos da defini¸c˜ao de valor absoluto:
|x| =
x se x ≥ 0
−x se x < 0
Vamos inicialmente desconsiderar o valor a = 0 do dom´ınio de f e analisar
a diferenciabilidade para R − {0}.
11

12. • Iniciemos analisando f para x < 0
lim
h→0
|x + h| − |x|
h
= lim
h→0
−(x + h) − (−x)
h
= lim
h→0
−x − h + x
h
=
lim
h→0
−h
h
= −1
desde que h seja suficientemente pequeno para que x+h < 0, e portanto
|x + h| = −(x + h).
• Agora vamos analisar a diferenciabilidade de f para x > 0
lim
h→0
|x + h| − |x|
h
= lim
h→0
x + h − x
h
= lim
h→0
h
h
= 1
desde que h seja suficientemente pequeno para que x+h > 0, e portanto
|x + h| = x + h.
Isso significa que a fun¸c˜ao f ´e diferenci´avel nos intervalos (−∞, 0) e
(0, +∞), mas ainda h´a a necessidade de analisar a diferenciabilidade de f
para o n´umero a = 0. Ser´a que esta fun¸c˜ao ´e diferenci´avel em a = 0?
Para isso devemos verificar se este limite existe para a = 0:
lim
h→0
|a + h| − |a|
h
• Assim, vamos come¸car pelo limite lateral esquerdo. Neste caso, x < 0
e o limite fica
lim
h→0−
|0 + h| − |0|
h
= lim
h→0−
−(0 + h) − 0
h
= lim
h→0−
−h
h
= −1
• O limite lateral direito, com x > 0, fica
lim
h→0+
|0 + h| − |0|
h
= lim
h→0+
0 + h − 0
h
= lim
h→0+
h
h
= 1
Logo, como os limites laterais s˜ao diferentes, o limite pontual n˜ao existe
e a fun¸c˜ao n˜ao ´e diferenci´avel em a = 0. Assim, a fun¸c˜ao f ´e diferenci´avel
em R − {0}.
12

13. CONDIC¸ ˜OES DE DIFERENCIABILIDADE
Teorema: Se uma fun¸c˜ao f for diferenci´avel (deriv´avel) em a, ent˜ao f ´e
cont´ınua em a.
Assim, podemos definir as seguintes condi¸c˜oes para determinar que uma
fun¸c˜ao f n˜ao ´e diferenci´avel em um n´umero a:
1. O teorema nos diz que se f apresenta descontinuidade em a, ent˜ao f
n˜ao ´e diferenci´avel em a.
2. Se o gr´afico da fun¸c˜ao f possuir uma “dobra” em a, n˜ao existir´a tan-
gente neste ponto e a fun¸c˜ao n˜ao ser´a diferenci´avel. Por exemplo,
f(x) = |x|, que apresenta uma dobra em a = 0, como mostra o gr´afico
a seguir.
3. Se existir uma reta tangente vertical em x = a, ou seja,
lim
x→a
|f (x)| = ∞
ent˜ao f n˜ao ´e diferenci´avel em a.
EXEMPLOS
A) Seja a fun¸c˜ao
f(x) =



−x se x ≤ −1
5 − x2
se − 1 < x ≤ 2
2x − 3 se 2 < x < 3
5 se x = 3
2x − 3 se x > 3
cujo gr´afico ´e mostrado na seguinte figura.
13

14. A fun¸c˜ao possui descontinuidades nos n´umeros x = −1 e x = 3. Al´em
disto, ela possui uma “dobra” em x = 2. Assim, pelos quesitos 1 e 2 das
condi¸c˜oes de diferenciabilidade, a fun¸c˜ao n˜ao ´e diferenci´avel nos n´umeros
{−1, 2, 3}.
B) Seja a fun¸c˜ao f(x) = 3
√
x, em a = 0.
f (0) = lim
x→0
f(x) − f(0)
x − 0
= lim
x→0
3
√
x − 3
√
0
x
= lim
x→0
x1/3
x
= lim
x→0
1
x2/3
= +∞
Logo, a fun¸c˜ao n˜ao ´e diferenci´avel em a = 0 pelo quesito 3 das condi¸c˜oes
de diferenciabilidade.
Observe no gr´afico a seguir como a fun¸c˜ao apresenta tangente com in-
clina¸c˜ao infinita na origem.
14

15. 6 Derivadas de ordem mais alta
Se f for diferenci´avel, ent˜ao sua derivada f ´e uma fun¸c˜ao que tamb´em
pode ter sua pr´opria derivada, chamada de segunda derivada ou derivada de
ordem dois de f.
d
dx
dy
dx
=
d2
y
dx2
f (x) = (f ) (x) = lim
h→0
f (x + h) − f (x)
h
Retornando ao problema da velocidade, a segunda derivada da fun¸c˜ao
f, que relaciona momentos do tempo em posi¸c˜oes de um corpo no espa¸co,
representa a acelera¸c˜ao, a varia¸c˜ao da velocidade, que ´e dada pela fun¸c˜ao v,
v(t) =
d
dt
f(t)
a =
d
dt
v(t) =
d2
dt2
f(t)
A terceira derivada de f ´e a derivada da segunda derivada,
f (x) =
d
dx
d2
dx2
f(x) =
d3
dx3
f(x)
15

16. No caso do problema da velocidade, a terceira derivada representa o so-
lavanco ou sacudida, que ´e a varia¸c˜ao da acelera¸c˜ao em rela¸c˜ao ao tempo.
EXEMPLO
Seja f(x) = 3x2
+ 1. Determine f e f .
f (x) = lim
h→0
3(x + h)2
+ 1 − (3x2
+ 1)
h
=
lim
h→0
3(x2
+ 2hx + h2
) + 1 − 3x2
− 1
h
= lim
h→0
3x2
+ 6hx + 3h2
− 3x2
h
=
lim
h→0
6hx + 3h2
h
= lim
h→0
(6x + 3h) = 6x
f (x) = lim
h→0
6(x + h) − 6x
h
= lim
h→0
6x + 6h − 6x
h
= lim
h→0
6h
h
= 6
16