Este documento apresenta um resumo do conteúdo de Matemática Aplicada à Economia ministrado pelo professor Francisco Leal Moreira. O documento aborda tópicos como funções de duas variáveis como domínio, imagem e curvas de nível; derivadas parciais de primeira e segunda ordem; máximos e mínimos de funções; integral indefinida e definida; e sua aplicação em conceitos econômicos como custo, produção, utilidade e demanda.

1. PONTIFÍCIA UNIVERSIDADE CATÓLICA
DO RIO GRANDE DO SUL
FACULDADE DE MATEMÁTICA
MATEMÁTICA APLICADA À ECONOMIA
Prof. Francisco Leal Moreira
2011/1

3. SUMÁRIO
1. FUNÇÕES DE DUAS VARIÁVEIS
1.1. FUNÇÕES HOMOGÊNEAS
1.2. CURVAS DE NÍVEL
1.3. SITE RELACIONADO
1.4. RESPOSTAS
2. DERIVADAS DE FUNÇÕES DE DUAS VARIÁVEIS
2.1. INTERPRETAÇÃO GEOMÉTRICA DAS DERIVADAS PARCIAIS
2.2. TAXAS DE VARIAÇÃO
2.3 ELASTICIDADE
2.4. DERIVADAS PARCIAIS DE SEGUNDA ORDEM
2.5. HESSIANO
2.6. REGRA DA CADEIA(RC)
2.7. FUNÇÃO IMPLÍCITA
2.8. DERIVAÇÃO IMPLÍCITA
2.9. TAXA MARGINAL DE SUBSTITUIÇÃO
2.10. SITES RELACIONADOS
2.11. RESPOSTAS
3. DIFERENCIAIS
3.1. INTERPRETAÇÃO GEOMÉTICA DA DIFERENCIAL
3.2. DERIVADA COMO UM QUOCIENTE
3.3. DIFERENCIAL TOTAL
3.4. RESPOSTAS
4. ANÁLISE DO COMPORTAMENTO DE UMA FUNÇÃO
4.1. PONTO CRÍTICO
4.2. FUNÇÃO CRESCENTE E FUNÇÃO DECRESCENTE
4.3. DETERMINAÇÃO DOS INTERVALOS DE CRESCIMENTO E DECRESCIMENTO
4.4. DETERMINAÇÃO DOS EXTREMOS RELATIVOS DE UMA FUNÇÃO
4.4.1. TESTE DA DERIVADA PRIMEIRA(TDP)
4.4.2. TESTE DA DERIVADA SEGUNDA(TDS)
4.5. CONCAVIDADE E INFLEXÃO
4.5.1. TESTE DA CONCAVIDADE
4.5.2. PONTO DE INFLEXÃO
4.6. TAXA DE VARIAÇÃO DE UMA TAXA DE VARIAÇÃO
4.7. WINPLOT
4.8. SITES RELACIONADOS
4.9. RESPOSTAS
5. MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS
5.1. PONTO CRÍTICO DE UMA FUNÇÃO DE DUAS VARIÁVEIS
5.2. CRITÉRIO PARA CARACTERIZAÇÃO DE PONTOS EXTREMANTES
5.3. MÁXIMOS E MÍNIMOS CONDICIONADOS
5.3.1. MÉTODO DA SUBSTITUIÇÃO
5.3.2. MÉTODO DOS MULTIPLICADORES DE LAGRANGE
5.4. SITES RELACIONADOS
5.5. RESPOSTAS
6. INTEGRAL INDEFINIDA
6.1. PRIMITIVA
6.2. INTERPRETAÇÃO GEOMÉTRICA DA INTEGRAL INDEFINIDA
6.3. REGRAS DE INTEGRAÇÃO
6.4. SITES RELACIONADOS
6.5. RESPOSTAS
7. INTEGRAL DEFINIDA
7.1. PROPRIEDADES BÁSICAS
7.2. INTERPRETAÇÃO GEOMÉTRICA DA INTEGRAL DEFINIDA
7.3. ÁREA DA REGIÃO ENTRE DUAS CURVAS
1
3
4
5
6
9
11
12
13
15
16
17
18
19
21
22
22
24
25
26
27
29
30
31
31
31
32
32
33
34
34
34
36
37
38
38
40
41
42
43
44
45
46
47
48
48
48
49
55
56
58
59
60
61

4. 7.4. EXCEDENTE DO CONSUMIDOR
7.5. EXCEDENTE DO PRODUTOR
7.6. SITES RELACIONADOS
7.7. RESPOSTAS
8. BIBLIOGRAFIA
9. APÊNDICE
1.CONJUNTO DOS NÚMEROS REAIS
2. OPERAÇÕES COM FRAÇÕES
3. SIMPLIFICAÇÃO DE FRAÇÕES
4. INTERVALOS
5. OPERAÇÕES COM CONJUNTOS
6. PRODUTOS NOTÁVEIS
7. FATORAÇÕES COMUM E DIFERENÇA DE DOIS QUADRADOS
8. RESOLUÇÃO DE EQUAÇÕES DE 1O GRAU
9. RESOLUÇÃO DE EQUAÇÕES DE 2O GRAU
10. PRODUTO NULO
11. RESOLUÇÃO DE INEQUAÇÕES DO 1O GRAU
12. RESOLUÇÃO DE SISTEMAS DE EQUAÇÕES DO 1O GRAU
13. POTÊNCIAS
14. EQUAÇÃO PONTO-DECLIVIDADE
15. IMAGEM DE UMA FUNÇÃO NUM PONTO
16. RESPOSTAS
17. DERIVADAS DE FUNÇÕES DE UMA VARIÁVEL
17.1. DERIVADA DE UMA FUNÇÃO OU FUNÇÃO DERIVADA
17.2. REGRAS DE DERIVAÇÃO
17.3. INTERPRETAÇÃO GEOMÉTRICA DA DERIVADA DE UMA FUNÇÃO NUM PONTO
17.4. APLICAÇÕES DE DERIVADAS
17.5. SITES RELACIONADOS
17.6. RESPOSTAS
18. BIBLIOGRAFIA
64
65
66
66
67
68
68
69
69
70
71
72
73
73
74
75
75
76
77
78
79
80
82
82
82
87
88
90
90
92

5. 1. FUNÇÕES DE DUAS VARIÁVEIS
Uma função f de duas variáveis é uma relação que a cada par ordenado de números reais (x,y) faz
corresponder um único número real f(x,y).
Exemplo:
Seja a função dada por f(x,y) = x 2
y 2 . Determine f(0,0), f(–1, –1), f(1,2), Dom f e Im f.
Solução:
a) f(0,0) = 0 2
02
0
b) f(–1, –1) = ( 1) 2
0
( 1) 2
c) f(1,2) = 12
2
d) O domínio de uma função de duas variáveis é o conjunto de pares ordenados do
tem sentido, neste caso, para os quais a f(x,y) = x 2
(x,y)
2
, o Dom f =
2
2
22
5
para os quais a função
y 2 é um número real. Como x2 +y2
0, para qualquer
.
e) A imagem de f é o conjunto formado pelas imagens de todos os elementos do domínio de f, neste caso, como a
imagem de qualquer (x,y)
2
O gráfico de f é a superfície do
par é dada por f(x,y) = x 2
3
y2
0, a im f =
.
que apareça abaixo.
z
y
x
Observação:
As funções de três ou mais variáveis não podem ser representadas graficamente.
1

6. E1) Seja a função dada f(x,y) = x2 + y2 (duas variáveis). Encontre:
1) f(1,2)
3) f(–3, –4)
2) f(0,0)
O gráfico de f é uma superfície do
3
4) Dom f
5) Im f
(parabolóide abaixo).
z
y
x
E2) Seja a função dada por f(x,y) =
1) f(1,0)
2) f(3, –7)
1
E3) Seja f(x,y) =
x
1) f(1,0)
2
3x
. Determine:
y x
3) f(1, –1)
4) Dom f
5) a representação gráfica do Dom f
4) Dom f
5) a representação gráfica do Dom f
. Determine:
y
2) f(3, –7)
3) f(1, –1)
E4) Represente graficamente os domínios das seguintes funções :
1) f(x,y)= x y 1
2) f ( x, y)
1
2x y 1
3) f(x,y)= ln (x2- y + 1)
4) f(x,y) =
ln x
x 1
E5) Uma loja vende apenas dois produtos, o primeiro a 50 u.m. a unidade e o segundo a 60 u.m. a unidade.
Sejam x e y as quantidades vendidas dos dois produtos. Determine:
a)função receita
b)a representação gráfica dos pontos (x,y) para os quais a receita é 300 u.m.
2

7. 1.1. FUNÇÕES HOMOGÊNEAS
Uma função z = f( x1, x 2...x n ) é dita homogênea de grau m se,
0, f( x 1 , x 2 ... x n ) =
m
f( x1, x 2...x n ).
Interpretação:
Se uma função f é homogênea de grau m, multiplicando-se as variáveis independentes por um certo
número real
(lambda) positivo, o valor da função f ficará multiplicado por
m
.
Exemplo:
Verifique se a função dada por f(x,y) = x 3
y 3 é homogênea, em caso afirmativo determine o grau.
Solução:
f (λx, λy)
(λx) 3
(λy) 3
λ3x3
λ3y3
λ 3 (x 3
y3 )
λ 3 (x 3
y3 )
λ 3 / 2 .f ( x, y)
Logo, a função f é homogênea de grau 3/2.
Observação:
Como f (λx, λy)
λ 3 / 2 .f ( x, y) , se multiplicarmos, por exemplo, x e y por 4, a f(x,y) ficará multiplicada
por 8, isto é, f(4x,4y) = 4 3 / 2.f ( x, y) 8.f ( x, y) .
E6) Uma função f é homogênea de grau 2. Se f(5) = 20, encontre f(15).
E7) Uma função f é homogênea de grau –1. Se f(2,3) = 4, encontre f(10.15).
E8) Uma função f é homogênea de grau –2. Se f(4,2) = 10, encontre f(2,1).
E9) Verifique se as funções abaixo são homogêneas, em caso afirmativo determine o grau.
1) f(x,y) = x – y
2) f(x) = 2x –1
3) f(x,y) = xy
4) f(x,y) = 2x + 3y
5) f(x,y) = xy – x2
6) f(x,y) = xy + 5x
7) f(x,y) = 2x 2 + 3xy – y2
8) f(x,y) =
11) f(x,y) = y3 + 4xy2 + 3x2
12) f(x,y) =
9) f(x,y) = x 4
2y 4
10) f(x,y) = 5 6 xy 2
2x
3y
10x 3y
2x 2
x
.
x 2y
1)Determine e represente graficamente o domínio da f;
E10) Seja a função dada por f(x,y) =
2)f é homogênea ? Em caso afirmativo determine o grau;
E11) Uma função P = f(x,y) é homogênea do grau –1. Por quanto devem ser multiplicados x e y para
que P seja multiplicada por 2 ?
3

8. 1.2. CURVAS DE NÍVEL
Ck = (x, y)
2
/ f ( x , y)
k
Exemplo:
Seja a função dada por z= x2 + y2 . Determine as curvas de nível para z = 1 , z =2 , z = 3 e z = 4.
Solução:
z=1
x2 + y2 = 1 (circunferência de centro C(0,0) e raio 1 )
z=2
x2 + y2 = 2 (circunferência de centro C(0,0) e raio
2 )
z=3
x2 + y2 = 3 (circunferência de centro C(0,0) e raio
3 )
z=4
x2 + y2 = 4 (circunferência de centro C(0,0) e raio 2 )
Mapa de curvas de nível
y
x
Observação: As curvas de nível nunca se interceptam.
Gráfico da Função (parabolóide)
z
y
x
4

9. E12) Esboce as curvas de nível das funções:
1) z = y – x2 para z = 0, z =1 e z =2
2) z = y – x para z = 0, z =2 e z =4
3) z = y – ln x para z = 0, z =1 e z =2
E13) Seja a função dada por z = 4 x 2
y 2 . Faça as curvas de nível para z = 0, z = 1 e z = 2
E14) Seja C(x,y) = 2x + 3y + 5 a função Custo Total para dois produtos de quantidades x e y. Faça as curvas
de nível para C = 11 , C = 17 , C = 23 e C = 29.
As curvas de nível da função Custo são denominadas curvas de isocusto, pois representam as combinações
de quantidades x e y que possuem o mesmo custo.
E15) Seja P(x,y) = x2.y a função Produção de uma empresa, onde x e y são quantidades de insumos(mão–
de-obra e capital). Faça as curvas de nível para P = 10 e P = 20.
As curvas de nível da função Produção são denominadas isoquantas, pois representam as combinações
de quantidades x e y que correspondem a mesma produção.
E16) Seja U(x,y) = xy a função que dá a utilidade de um consumidor que deseja adquirir dois produtos em
quantidades x e y. Faça as curvas de nível para U = 2 e U = 4.
As curvas de nível da função Utilidade são denominadas curvas de indiferença, pois representam as
combinações de quantidades x e y que fornecem o mesmo nível de utilidade ou satisfação ao consumidor.
E17) Seja q1( p1, p2 ) = –p12 + p2 + 2 a função Demanda de um produto em função do próprio preço p 1 e do
preço p2 de outro produto que lhe é substituto.
Faça as curvas de nível para q 1 = 0 , q1 = 2 e q1 = 4.
As curvas de nível da função Demanda são denominadas curvas de isodemanda, pois representam as
combinações de preços p1 e p2 que determinam a mesma demanda do produto de quantidade q 1.
1.3. SITE RELACIONADO
www.uel.br/revistas/geografia/V14N1/Artigo15.pdf
5

10. 1.4. RESPOSTAS
E1) 1) 5
2) 0
E2) 1) –3
2) -
E3) 1) 1
2)
3) 25
4)
2
5) [0,
)
9
10
3)
3
2
4) {( x, y)
2
/y
x}
1
4
3)
2
2
4) {( x, y)
2
/y
x 2}
E4) 1) {( x, y)
2
/y
x 1}
2) {( x, y)
3) {( x, y)
2
/y
x 2 1}
4) {( x, y)
2
2
/y
2x 1}
/x
0 e x 1}
y
5
E5) 1) R = 50x + 60y
2)
0
6
x
E6) 180
E7) 0,8
E8) 40
E9) 1) Sim, grau 1
2) Não
3) Sim, grau 2
4) Sim, grau 1
5) Sim, grau 2
6) Não
7) Sim, grau 2
8) Sim, grau 0
9) Sim, grau 2
E10) 1) {( x, y)
E11)
2
10) Sim, grau 0,6
/ x 2y
0}
11) Não
2) Sim, grau 0
1
2
6
12) Sim, grau –1

11. E12) 1)
2)
3)
y
y
y
x
x
E13)
y
x
E14)
y
x
E15)
7
x

12. y
x
E16)
y
x
E17)
p2
p1
8

13. 2. DERIVADAS DE FUNÇÕES DE DUAS VARIÁVEIS
f (x
Se y = f(x) é uma função de uma variável real, sua derivada f ’(x) = lim
x
x) f (x)
pode ser
x
0
interpretada como a taxa de variação de y em relação a x ou como a função declividade da reta tangente
ao gráfico de f.
Se z = f(x,y) é uma função de duas variáveis, podemos falar em duas derivadas, por isso, denominadas
derivadas parciais. Uma derivada parcial é obtida quando x varia e y permanece constante e, a outra, quando
y varia e x permanece constante.
As derivadas parciais de f em relação a x e a y são denotadas por fx ou
por fx(x,y) = lim
x
Nota:
f (x
0
x , y ) f ( x , y)
x
é uma variante da letra grega
e
fy(x,y) = lim
y
f ( x, y
0
f
e fy ou
x
f
e são definidas
y
y) f ( x, y)
y
(delta minúsculo).
Exemplo:
Seja a função dada por f(x,y) = x2 + y2 – 2x3y + 5xy4 – 1 . Determine as derivadas parciais de f.
Solução:
f
(x,y) = 2y – 2x3 + 20xy3
y
f
(x,y) = 2x – 6x2y + 5y4
x
E1) Determine as derivadas parciais
1) z = 4x2y – 5x3y2 + 2x – y
4) z =
x2
y2 1
7) z = (2x – y)exy
z
e
x
z
das funções:
y
2) z = x y
5) z =
2xy
3x 2 y
8) z = 2x2y.ln 2y
9
3) z = ln(xy2)
6) z =
9) z =
2 x 3y
x2
1
x
4y
1
+ ln exy
2y

14. E2)Sejam px = 8 – x e py = – 2y + 34 as equações da demanda para dois produtos de quantidades x e y.
Se C = 8 + 4x + 6y é a função Custo associada, determine a função Lucro e as funções Lucro Marginal.
E3) Seja z
x 0,75 .y 0,25 uma função Produção. Determine as funções Produção Marginal.
Nota: Dois produtos são chamados de produtos substitutos se o aumento da demanda de um resulta na
diminuição da demanda do outro. Produtos substitutos são competitivos, como manteiga e margarina. Dois
produtos são chamados de produtos complementares se o aumento da demanda de um resulta no aumento
da demanda do outro. É o caso, de câmaras fotográficas e filmes fotográficos. .
E4) Se qx = –px –2py + 10 a função que descreve a demanda de um produto em função do seu preço p x e do
do preço de outro produto. Esses produtos são substitutos ou complementares ? Por que ?
E5) A produção semanal de certa fabrica é dada pela função P(x,y) = 1200x + 500y + x 2y –x3 – y2 unidades,
onde x é o número de operários especializados e y o número de operários não-especializados no trabalho.
No momento, a mão-de-obra disponível é constituída por 30 operários especializados e 60 operários nãoespecializados.
1) Determine as funções produção marginal.
2) Use os métodos de análise marginal(uso de uma derivada parcial) para estimar a variação da produção
se mais um operário especializado for contratado.
3) Calcule a variação exata da produção, caso o operário especializado seja contratado.
E6) Um fabricante estima que a produção mensal de certa fábrica é dada pela função de Cobb-Duglas
P(K,L) = 50K0,4L0,6 , onde K é o capital imobilizado em milhares de reais e L é o volume de mão-de-obra
em homens-hora:
1) Determine as funções produtividade marginal, para um capital imobilizado de R$ 750.000,00 e um
volume de mão-de-obra de 991 homens-horas.
2) O fabricante deve aumentar o capital imobilizado ou o volume de mão-de-obra para aumentar mais
rapidamente a produção ?
10

15. 2.1. INTERPRETAÇÃO GEOMÉTRICA DAS DERIVADAS PARCIAIS
Considere a superfície abaixo, gráfico de uma função z = f(x,y).
Para y = k (constante) a função f se reduz a uma função de uma variável x, z = f(x,k).
z
t
z = f(x,y)
P
y1= k
0
y
x1
x
z= f(x,k)
Portanto, a derivada parcial de f em relação a x no ponto (x 1,y1) representa a declividade da superfície no
ponto (x1,y1) na direção paralela ao eixo x, isto é
f
(x1,y1) = at
x
Analogamente , a derivada parcial de f em relação a y no ponto (x 1,y1) representa a declividade da
superfície no ponto (x1,y1) na direção paralela ao eixo y, isto é
f
(x1,y1) = at
y
Exemplo:
Encontrar a declividade da reta tangente à curva resultante da intersecção de: f(x,y) = x 2 + y2 – 2x3y + 5xy4– 1
com o plano x = –1 no ponto (–1,1, –2).
Solução:
A intersecção do plano com o gráfico da f é uma curva com a direção do eixo y, logo at =
Como
f
(x1,y1).
y
f
f
(x,y) = 2y – 2x3 + 20xy3 e
(–1,1) = –16, a declividade da reta tangente é a = –16.
y
y
E7) Encontrar a declividade da reta tangente à curva resultante da intersecção de:
1) z = x2 + y2 com o plano x = 1, no ponto ( 1,2,5)
2) z = x2 + y2 com o plano y = 2, no ponto (2,2,8)
3) z = 34
9x 2
4 y 2 com o plano y = 2, no ponto (1,2,3)
11

16. 1
E8) Dada a função f(x,y) = y 2
x
2
, determine :
y2
1) o domínio de f
2) f x(3,4)
3) f y(3,4)
4) o coeficiente angular da reta tangente à curva que é a intersecção do gráfico de f com o plano x = 3 no
ponto em que y = 4.
E9) Seja a função dada por f(x,y) = x y
1)Represente graficamente o domínio da f.
2)Encontre
f
.
y
3) f é homogênea ? Em caso afirmativo determine o grau.
E10) Seja a função dada por f(x,y) =
x2
3xy y 2
y x
1) Determine e represente graficamente o domínio da f.
2) Verifique se f é homogênea, em caso afirmativo, determine o grau.
3) Encontre
f
x
2.2. TAXAS DE VARIAÇÃO
f
fornece a taxa de variação de f(x,y) em relação à x para y = k (constante), isto é, mede a taxa de variação
x
de f(x,y) quando (x,y) se move na direção do eixo x.
f
fornece a taxa de variação de f(x,y) em relação à y para x = k (constante), isto é, mede a taxa de variação
y
de f(x,y) quando (x,y) se move na direção do eixo y.
E11) Uma placa de metal aquecida está situada em um plano xy de modo que a temperatura T no ponto (x,y)
é dada por T(x,y) =10( x2 + y2 )2 . Determine a taxa de variação de T em relação à distância no ponto
P(1,2) na direção:
1) do eixo das abscissas
2) do eixo das ordenadas
12

17. 2.3 ELASTICIDADE
Seja y = f(x) uma função.
y
y+ y
f
y
0
Da figura acima, observa-se que uma variação
A variação relativa em x é
x+ x
x
x
x em x corresponde uma variação
y em y.
y
x
e a variação relativa em y é
.
x
y
y
y
y x
y x
.
. .
A variação relativa média em y por unidade de variação relativa em x é
(1)
x
y
x
x y
x
f(x Δx) f(x) x
. , cujo limite quando x tende
Como y = f(x+ x ) – f(x), podemos escrever a (1) como
Δx
y
f (x
a zero é lim
x
0
dy x
x) f (x) x
x
. .
. = f’(x). ou
x
y
y
dx y
Este limite fornece a variação percentual aproximada da função correspondente a uma variação de 1% em x.
Se y = f(x) representar a função demanda, onde x representa o preço unitário de venda do produto, então o
produto
dy x
é denominado elasticidade-preço da demanda e representado por e.
.
dx y
e=
dy x
.
dx y
Exemplo:
Seja q = 110 – 4p2 a equação da demanda para um certo produto, onde q é a quantidade demandada e
P é o preço unitário do produto. Determine:
a) a variação relativa da demanda quando o preço da unidade passa de 5 u.m. para 5,1 u.m.,
b) use o resultado anterior para obter uma aproximação da elasticidade da demanda para o preço de 5 u.m.,
c) calcule a elasticidade da demanda em relação ao preço de 5 u.m.
13

18. Solução:
a) A variação relativa da demanda é dada por
q
.
q
Para p =5, q = 10 e, para p = 5,1; q = 5,96, logo,
q = -4,04 e
q
4,04
=
= -0,404.
10
q
Portanto, a demanda terá um decréscimo de 40,4 %.
b) Um aumento de 2% no preço p, representa um decréscimo de 40,4% na demanda. Portanto, um aumento
de 1% no preço p, representará um decréscimo de
c) A elasticidade da demanda é dada por e =
Como
dq
dp
-8p
e = -8p.
40,4
= 20,2 % na demanda.
2
dq p
. .
dp q
p
8p 2
=
. Para p = 5 e q = 10, temos e = -20
q
q
Um acréscimo(ou decréscimo) de 1 % no preço no preço unitário 5, representará um decréscimo(ou aumento)
aproximado de 20% na demanda.
Seja q = f(p1,p2) a equação da demanda de um certo produto em função do seu preço p 1 e do preço p2 de
outro produto .
e
q p1
.
p1 q
ec
q p2
.
p2 q
A elasticidade e representa, aproximadamente, a variação percentual da demanda decorrente da variação
de 1% no preço .
Observação:
Quando a quantidade demandada de um produto é expressa em função do preço de outro produto, a
elasticidade é chamada de elasticidade cruzada.
14

19. Exemplo:
2
Seja q1 = p1
p 2 10 a função que descreve a demanda de um certo produto em função do seu preço p1 e do
Preço p2 de outro bem. Determine a elasticidade da demanda em relação ao preço p2, para p1 = 2 e p2 = 3 e
interprete o resultado obtido.
Solução:
Estamos interessados, nesse caso, na elasticidade cruzada, portanto: e c
q1
p2
1 , q1= – 22 – 3 + 10 = 3 e
p2
q1
3
3
ec
1.
3
3
q1 p 2
.
.
p 2 q1
1
Interpretação: Se o preço p2 aumentar 1%, a demanda do produto de quantidade q 1 vai cair aproximadamente
1%(produtos complementares).
E12) Seja q1 = 200 0,6p1
0,3p 2 a equação que descreve a demanda da manteiga em função do seu preço
p1 e do preço p2 da margarina. Suponha que os preços desses produtos são p 1 = 300 e p2 = 200.
1) Determine a elasticidade da demanda da manteiga em relação ao próprio preço.
2) Determine a elasticidade da demanda da manteiga em relação ao preço da margarina.
E13) Se qx = – px – 2py + 10 a função que descreve a demanda de um produto em função do seu preço p x e do
preço py de outro produto, determine a elasticidade da demanda em relação ao preço py .
2.4. DERIVADAS PARCIAIS DE SEGUNDA ORDEM
Derivadas puras:
x
f
x
2
x
Derivadas mistas ou cruzadas:
f
2
x
f xx ;
f
y
y
2
f
y
f
f yy
y2
2
f
x y
f yx ;
y
f
x
2
f
y x
f xy
Observação:
As derivadas parciais de segunda ordem mistas, são iguais para funções continuas com derivadas parciais
continuas.
15

20. Exemplo:
Encontrar as derivadas parciais de segunda ordem da função dada por f(x,y) = x 2 + y2 – 2x3y + 5xy4– 1
Solução:
2
f
f
x2
( x , y)
2 6y
(x,y) = 2x – 6x2y + 5y4
x
2
f
( x , y)
y x
2
f
(x,y) = 2y – 2x3 + 20xy3
y
f
y2
( x , y)
6x 2
20 y 3
2 60xy 2
2
f
( x , y)
x y
6x 2
20 y 3
E14) Determinar as derivadas parciais de segunda ordem das funções dadas por:
1) z = x2y – xy2 + 2x – y
5) z =
2y
x
xy2
2) z = xy
3) z = ln(xy)
4) z = e
6) z = x3y2
7) z = xe-y
8) z = xln exy
x
.
y
1) Encontre as derivadas parciais de segunda ordem da z.
E15) Seja a função dada por z =
2) A função f é homogênea ? Em caso afirmativo, determine o grau de homogeneidade.
2.5. HESSIANO
Chama-se Hessiano da função z = f(x,y) a função H(x,y) =
f xx ( x, y)
f xy ( x, y)
f yx ( x, y)
f yy ( x, y)
Exemplo:
Calcule o Hessiano da função dada por f(x,y) = 2x3y2 + 4x2y4– 3 no ponto (1, -1)
16

21. Solução:
f xx ( x, y) 12xy 2
fx(x,y) = 6x2y2 + 8xy4
f xy ( x, y) 12x 2 y 32xy 3
21xy 2
2
8y 4
12x y 32xy
4x 3
f yy ( x, y)
fy (x,y) = 4x3y + 16x2y3
H(x,y) =
8y 4
48x 2 y 2
f yx ( x, y) 12x 2 y 32xy 3
12x 2 y 32xy 3
3
4x
3
2
48x y
2
H(1,-1) =
29
44
44
44
= 1276-1936=-660
E16) Calcule o Hessiano da função dada por:
1)f (x,y) = x3 – y3 + 2xy – 1 no ponto (2, – 1)
2) f(x,y) = x2y3 + 2xy – 4x + 3y – 5 no ponto (– 1, – 1)
2.6. REGRA DA CADEIA(RC)
a) Se y = f(u) e u=g(x), isto é, u é função de x, então
b) Se z = f(x,y) , onde x = g(t) e y = h(t) então
dz
dt
dy
dx
dy du
.
du dx
f dx
.
x dt
f dy
.
y dt
Considere o seguinte problema:
Se z = x2y + 2xy2 , onde x = 2t e y = t2, encontre
dz
para t = 1.
dt
Como x e y dependem de t, podemos escrever z como função de uma única variável t .
z = 4t4 + 4t5 e daí,
Logo,
dz
= 16t3 + 20t4.
dt
dz
(1) = 36
dt
E17) Use a Regra da Cadeia para calcular
E18) Determine
dz
(1) do problema acima.
dt
dz
, sendo:
dt
1) z = x2 + xy – y2 , x = 1 – t , y = et
2) z = x2y + xy – 3 , x = – t , y = ln t
17

22. 2.7. FUNÇÃO IMPLÍCITA
Uma função dada na forma y = f(x) é chamada função explícita porque y está explicitado, isto é, isolado.
Por exemplo, as equações y = x2 –3 e y = –2x – 1 definem explícitamente duas funções.
y
y
x
x
Nem sempre uma função é definida explícitamente. Por exemplo, as equações y2 – x = 3, x2 + y2 = 4 e
x2 +2y3 = 3xy.
y
y
x
y
x
x
O gráfico da equação y2 – x = 3 pode ser pensado como os gráficos de, pelo menos, duas funções y = f(x).
Nesse caso, dizemos que estas funções são definidas implícitamente pela equação.
O gráfico da equação x2 + y2 = 4 pode ser pensado como os gráficos de, pelo menos, duas funções y = f(x).
Funções definidas implícitamente pela equação.
O gráfico da equação x2 +2y3 = 3xy pode ser pensado como os gráficos de, pelo menos, três funções y = f(x).
Funções definidas implícitamente pela equação.
Em determinadas condições, uma equação F(x,y) = 0 pode definir uma ou mais funções y = f(x). Nesse caso,
18

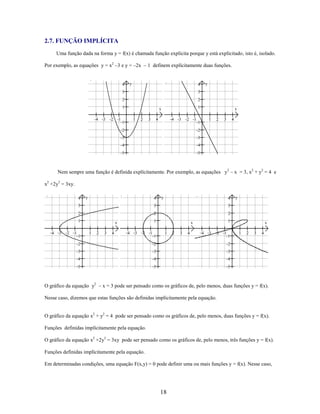
23. essas funções são denominadas funções implícitas definidas pela equação F(x,y) = 0. Do último exemplo,
podemos observar que nem sempre é possível explicitar y na equação, isto é, escrever a função na forma
explícita.
E19) Encontre uma função y = f(x) definida implicitamente por cada uma das equações abaixo.
2) x 2 + y2 – 4 = 0
1) 2x – xy +1 = 0
3) e y – x = 0
2.8. DERIVAÇÃO IMPLÍCITA
Vamos supor que numa aplicação, estamos interessados em analisar o comportamento de uma função
dy
y = f(x), definida implicitamente por uma equação F(x,y) = 0, isto é, precisamos da derivada
para estudar
dx
a função implícita f. Vamos admitir também, que seja impossível explicitar y na equação. Para resolver um
problema desse tipo observe o exemplo abaixo.
Exemplo:
Encontre
dy
de uma função y = f(x) definida implicitamente pela equação x2 +2y3 = 3xy.
dx
Solução:
Podemos encontrar a derivada
dy
= y’ de duas maneiras:
dx
1ª ) Derivação Implícita
Derivando ambos os membros: Dx( x2 + 2y3 ) = Dx3xy
Como Dx3xy é a derivada de um produto e Dx(y)p = Dx[f(x)]p = p.yp-1.y’, temos: 2x + 6y2.y’ = 3x.y’ + 3y
Isolando y’:. 6y2.y’ – 3x.y’ = 3y – 2x ou y’(6y2 – 3x) = 3y – 2x
Logo: y’ =
dy 3y 2 x
=
dx 6 y 2 3x
(1)
Esta fórmula é válida para todas as funções deriváveis que a equação x2 +2y3 = 3xy define implicitamente. Se
queremos, por exemplo, a derivada no ponto 1, devemos encontrar primeiro o correspondente valor de y na
equação x2 +2y3 = 3xy.
x=1
1 + 2y3 = 3y
Logo,
dy
3.1 - 2.1
(1) =
6.1 - 3.1
dx
2y3 – 3y + 1 = 0
y=1
1
3
19

24. 2ª ) regra da Cadeia
dz
dt
Se z = f(x,y) , onde x = g(t) e y = h(t) então
No caso, z = F(x,y) = 0 e y =h(x), segue que:
Como, neste caso,
dz
dx
0 , pois z = 0 e
dx
dx
dz
dx
f dy
.
y dt
f dx
.
x dt
F dx
.
x dx
1 , resulta: 0 =
F
=–
x
F dy
.
y dx
F
.1
x
F dy
.
y dx
F dy
.
y dx
F
dy
=– x
F
dx
y
Que é uma fórmula válida para todas as funções deriváveis que a equação F(x,y) = 0 define implicitamente.
Comparando com a situação anterior em que F(x,y) = x2 +2y3 – 3xy,
F
x
F
y
2x – 3y e
F
2 x 3y
3y 2 x
dy
=– x =– 2
=
F
dx
6 y 3x 6 y 2 3x
y
6y2 – 3x
(2)
Compare a (2) com a (1).
E20) Encontre as derivadas
1) 2xy – ln xy + 5 = 0
E21) Determine
dy
das funções y = f(x) definidas implicitamente pelas equações:
dx
2) 4x3y – 3xy2 – 6 = 0
3) 9x + 3y – 7xy2 – 8 = 0
dy
para a função ( 2x – 1 )4 + 10 = y2 + 20, dada em forma implícita.
dx
E22) Seja y = f(x) uma função dada implicitamente pela equação e xy + 3x = 3y3+ 4 . Encontre
dy
(1,0).
dx
E23) Seja y = f(x) uma função dada implicitamente pela equação ln (xy) = 2x – 2y2 . Encontre
dy
dx
20
(1,1).

25. 2.9. TAXA MARGINAL DE SUBSTITUIÇÃO
Se z = F(x,y) é uma função e z = k(constante) , a equação F(x,y) = k representa todas as combinações
de x e y que fornecem o mesmo valor k para a função F. Seja y = f(x) uma função definida implícitamente pela
equação F(x,y) = 0.
dy
TMS =
dx
F
x
F
y
A TMS representa, aproximadamente, a quantidade de y que pode ser substituída por uma unidade de x,
para que se tenha o mesmo valor k para a função.
Exemplo:
Encontre a TMS no ponto (4,3), onde U = 6xy + 9x +3y +3 é a função que dá a utilidade de um consumidor
de dois produtos de quantidades x e y. Interprete o resultado obtido.
Solução
U
= 6y + 9 e
x
U
= 6x + 3
y
U
x
U
y
dy
TMS =
dx
6y 9
, logo TMS(4,3) =
6x 3
27
= –1
27
Interpretação: A utilidade do consumidor no ponto (4,3), será aproximadamente a mesma se for substituída
uma unidade de y por uma unidade de x.
E24) Seja U = x2y a função utilidade de um consumidor que deseja adquirir dois produtos de quantidades x e y.
1) Calcule o valor da utilidade no ponto (4,5).
2) Encontre a TMS de x por y no ponto (4,5).
3) Qual a quantidade de y que pode ser substituída por uma unidade de x, em (4,5), usando y = f(x) ?
E25) Seja z =10x2y a função Produção de uma empresa que utiliza dois insumos em quantidades x e y.
Calcule a Taxa Marginal de Substituição no ponto (2,3).
21

26. 2.10. SITES RELACIONADOS
http://didisurf.googlepages.com/calculo2
http://didisurf.googlepages.com/calculo2
http://www.ucs.br/ccet/denq/prof/ana/deripar.htm
http://www.las.pucpr.br/anderson/arquivos/DERIVADAS%20PARCIAIS.pdf
http://www.pucrs.br/famat/demat/facin/calcb/material_200502/Topico_09_Derivadas_parciais.pdf
http://www.dmat.ufba.br/mat042/aula26/aula26.htm
http://www.sorocaba.unesp.br/professor/luiza/CDI-III/func3.pdf
http://www.esce.ips.pt/disciplinas/licenciatura/pe/materiais/Adm/Aulas%20Te%C3%B3ricas_elastic_T.Cons.pdf
http://www.uma.pt/ppereira/micro1200320042.ppt
http://books.google.com.br/books?id=lBQCU3svvFEC&pg=PA176&lpg=PA176&dq=taxa+marginal+de+substit
ui%C3%A7%C3%A3o&source=web&ots=OLa7rlQt_h&sig=QRZ-AlCYvRgkBGCbMA_zHLFh6hw&hl=ptBR#PPA255,M1
http://ube-164.pop.com.br/repositorio/1824/meusite/03%20-%20Teoria%20do%20Consumidor.ppt
2.11. RESPOSTAS
E1) 1) 8xy – 15x2y2 + 2 ; 4x2 – 10x3y – 1
x
2) y ;
3)
2 y
x
4)
x2
6)
y2 1
2x 2
(x
2
y
;
x2
6 xy 8 y
4 y)
2
;
5)
y2 1
3x 2
(x
2
8x
(3x 2 y) 2
;
6x 2
(3x 2 y) 2
7)exy(2xy – y2 + 2) ; exy(2x2 – xy – 1)
4 y) 2
8) 4xyln 2y ; 2x2(ln 2y + 1)
4y 2
9)Nota: ln exy = xy ,
1
x2
y ;
1
2y 2
x (ln exy = xy)
E2) L = – x2 – 2y2 + 4x + 28y – 8 , Lx = – 2x + 4 , Ly = – 4y + 28
E3) z x
0,75y 0, 25
x 0, 25
, zy
1 2
;
x y
0,25x 0,75
y 0,75
E4) Complementares
E5) 1) Px(x,y) = 1200 + 2xy – 3x2 , Py(x,y) = 500 + x2 – 2y
22
2) 2100
3)2069

27. E6) 1) 23,64 e 26,84
2) mão-de-obra
E7) 1) 4
2) 4
E8) 1)
2
{( 0,0)}
2
E9) 1) {( x, y)
3)
/ x y 0}
2
E10) 1) {( x, y)
3
125
2)
/x y
3) – 3
996
125
2) f y
0}
4)
996
125
1
3) Sim , grau 0,5
2 x y
2) Sim, grau 1
x2
3)
2y 2
(y x)
E11) 1) 200
2) 400
E12) 1) – 2,25
2) 0,75
2p y
E13) e c
px
2p y 10
E14) 1) 2y ; -2x ; 2x – 2y
4) y 4 e
xy2
; 2xe
xy2
2) 0 ; 0 ; 1
(2xy 2 1) ; 2e
xy2
(xy 3
5)
y)
7) 0 ; xe-y ; -e-y
E15) 1) zxx = 0 , zyy =
2x
y
3
y2
;0;
2
x2
6) 6xy2 ; 2x3 ; 6x2y
2) 2tln t – ln t + t – 1
1
x
2) y =
y
x
2)
4 x 2 ou y =
12 x 2 y 3y 2
4x 3
6 xy
3
2) – 2,5
4 x2
3) y = ln x
3)
1
5
E24) 1) 80
x
3
1
;0
y2
2) Sim , grau 0
E22) –3
E23)
4y
1
;
x2
2) – 4
E19) 1) y = 2 +
4(2x 1)
y
1
, zxy = zyx =
E18) 1) –2e2t – tet + 2t – 2
E21)
3)
8) 2y ; 0 ; 2x
E16) 1) 68
E20) 1)
2 xy
2
3) 1,8
E25) -3
23
9 7y 2
3 14xy

28. 3. DIFERENCIAIS
Se f é uma função dada por y = f(x), chamamos de diferencial de f a função dada por dy = f’(x) Δx onde x
está no domínio de f’e Δx é um acréscimo arbitrário de x.
Exemplo:
Se y = x4 – 8x2, então f(x) = x4 – 8x2 e f’(x) = 4x3 – 16x . Logo, da definição, dy = (4x3 – 16x) Δx .
Em particular, se x = –1, dy = 12 Δx .
Queremos definir agora, a diferencial da variável independente x, isto é a diferencial de y = x. Nesse caso,
dy = 1. Δx , como y = x, concluímos que dx = Δx .
Se f é uma função dada por y = f(x), a diferencial de x é definida por dx = Δx onde x está no domínio de f’e
Δx é um acréscimo arbitrário de x.
Assim, a diferencial de dy é uma função é obtida pela multiplicação da derivada f’(x) pela diferencial de x.
dy = f’(x)dx
Exemplo:
Se y = 3x2 – 2 então dy = 6xdx.
Em particular, se x = 3 e dx =–0,1; dy = –1,8.
E1)Use diferencial para encontrar um valor aproximado para a variação da área de um quadrado quando seu
lado passa de 2 cm para 1,8 cm.
E2) O raio de uma circunferência aumenta de 10 m para 10,1 m. Utilize diferencial para estimar o aumento
da área da circunferência. Compare essa estimativa com a variação
24
A.

29. 3.1. INTERPRETAÇÃO GEOMÉTICA DA DIFERENCIAL
y
f
f(x1 + Δx )
Q
t
Δy
T
dy
α
P
f(x1)
0
R
dx= Δx
x1 + Δx
x1
x
A medida do segmento orientado PR é dx = Δx .
A medida do segmento orientado RQ é Δy .
A declividade da reta t, tangente ao gráfico de f em P é a t = tg α =
med (RT )
med (PR )
Como at = f’(x1),
f’(x1) =
med (RT )
ou med (RT ) = f’(x1)dx
dx
med (RT )
dx
dy = med (RT ) .
Então, podemos dizer que dy é o acréscimo Δy caso seguíssemos a reta tangente t ao invés do gráfico de f.
Da figura acima, observa-se que a diferencial dy num ponto depende de Δx e, quanto menor for Δx mais
próximo dy estará de Δy .
Conclusão:
A diferencial de uma função pode ser usada para calcular aproximadamente variações da função, para
pequenos valores de Δx .
Exemplo:
Use diferenciais para aproximar o valor de
3
62 .
Solução:
dy = f’(x) dx e para Δx pequeno, Δy
dy
f(x+ Δx ) – f(x)
25
f’(x).dx
f(x+ Δx )
f’(x).dx + f(x)
(1)

30. Como queremos calcular a raiz cúbica de 62, a função f é f(x) =
3
x e a derivada de f é f’(x) =
1
3
.
3 x2
O valor mais próximo da
3
62 que conhecemos é
3
64
4 , logo, devemos considerar x = 64 e dx = -2.
1
Substituindo em (1) estes dados, temos: f(64+(-2))
3
3 64
Mas f(62) =
3
62 , logo
3
62
1
95
+4=
24
24
(-2) +
3
64
f(62)
2
2
+ 4.
3.16
3,953
Observação:
Uma calculadora fornecerá o valor será aproximado 3,952.
E3) Seja P = 0,1q3 – 2q uma função produção e q a quantidade de insumo. Use diferencial para calcular o
acréscimo aproximado da produção quando q passa de 10 para 10,2.
E4) Seja R = 100q – 2q2 uma função receita e q a quantidade vendida. Use diferencial para calcular a
variação aproximada da receita quando q passa de 30 para 31.
3.2. DERIVADA COMO UM QUOCIENTE
Da definição de diferencial dy = f’(x)dx, se dx
0, podemos escrever
dy
df ( x )
= f’(x) ou
= f’(x). Logo,a
dx
dx
derivada de y, em relação a x é igual à razão da diferencial de y, ou f(x), e a diferencial de x.
Observações:
a)
b)
dy
é a notação de Leibniz para derivada.
dx
d
pode ser interpretado como um operador da mesma forma que D x e, portanto, também é correto
dx
d
escrever
(y).
dx
Exemplo:
Se y = 2x3 – 5x2 + 6x – 1 então
dy d
=
(= 2x3 – 5x2 + 6x – 1) = 6x2 – 10x + 6
dx dx
26

31. E5) O raio de uma esfera metálica cresceu de 8,0 cm para 8,1 cm com aquecimento. Use diferencial para
calcular o acréscimo aproximado do volume.
E6) Encontre um valor aproximado para a variação da área de um Triângulo eqüilátero quando seu lado
passa de 4 cm para 4,001 cm.
E7) Um cubo de 10 cm de aresta cobriu-se uniformemente com uma camada de gelo de 0,1 cm de
espessura. Use diferencial para estimar o volume aproximado do gelo.
E8) O raio de uma esfera de aço mede 1,5 cm e sabe-se que o erro cometido na sua medição não excede
0,1 cm. O volume da esfera é calculado a partir da medida de seu raio. Estime o erro possível no cálculo
do volume.
E9) Use diferencial para aproximar:
a) 3 10
b) 4 80
c) 35
d)
5
32,2
3.3. DIFERENCIAL TOTAL
Analogamente ao que foi visto para função de uma variável, se z = f(x, y) é uma função de duas variáveis ,
definiremos os diferenciais dx e dy como variáveis independentes; ou seja podem ter qualquer valor. Então
o diferencial dz, também chamado de diferencial total, é definido por dz = fx (x,y) dx + fy (x,y) dy .
Assim dz é a variação de z, ao longo do plano tangente à superfície de equação z = f( x,y) em ( x0,y0,z0),
produzida pelas variações dx e dy em x e y respectivamente. Enquanto que
longo da superfície, produzida pelas variações de
x e
y em x e y, isto é,
z representa a variação de z ao
z
f (x
x, y
y) f ( x , y) .
E10) Seja z = 4.x3.y2. Determine dz.
E11) Determine a diferencial de f ( x , y)
x2
y 2 no ponto (4, 3).
E12) Utilize diferencial para estimar a quantidade de metal em uma lata cilíndrica fechada de 10cm de altura e
4cm de diâmetro se o metal das tampas de cima e de baixo têm 0,1 cm de espessura e o das laterais tem
espessura de 0,05cm.
27

32. E13) Calcule
z e dz para as seguintes funções, se:
b) f(x,y) = x 2
a) f(x,y) = 2 x 2 - 3xy varia de (1,2) a (1,01;2,02)
y 2 varia de (2,1) a (2,1;1,01)
E14) Calcule um valor aproximado para a variação da área de um triângulo retângulo quando seus catetos
passam de 4 cm para 4,1 cm e 3 cm para 2,8 cm.
E15) Considere uma caixa, com tampa, com a forma de um paralelepípedo retângulo de dimensões a = 2 cm ,
b = 3 cm c = 4 cm. Se as arestas sofrerem acréscimos de 1 % , 10 % e 2 %, respectivamente, determine:
a) o acréscimo aproximado do volume
b) o acréscimo exato do volume
E16) Use diferencial para calcular o aumento aproximado do volume de um cilindro circular reto, quando seu
raio varia de 2 cm para 2,1 cm e a altura varia de 6 cm para 6,2 cm.
E17) Considere um retângulo de lados a = 3 cm e b = 4 cm. Determine a variação aproximada da diagonal se
o lado a aumentar 0,01 cm e o lado b diminuir 0,2 cm.
E18) Mediram-se o raio e altura de um cilindro circular reto, obtendo-se 3 cm e 8 cm, respectivamente, com um
erro de medida possível de 0,1 cm. Use diferencial para obter uma aproximação do erro máximo no
volume calculado do cilindro.
E19) Considere um recipiente, com tampa, de forma cilíndrica, com dimensões: raio = 2 cm e altura = 5 cm. Se
o custo custo do material usado em sua confecção é de R$ 0,81 por cm2 e suas sofrerem um acréscimo de
10 % no raio e 2 % na altura, determine:
a) o valor aproximado do acréscimo no custo do recipiente
b) o valor exato do acréscimo no custo do recipiente
E20) Use diferencial para encontrar um valor aproximado para a expressão (1,001) 3,02.
28

33. 3.4. RESPOSTAS
E1) dA = - 0,8 cm2
E2) dA = 2 m2 ,
A = 2,01 m2 e = 0,01 m2
E3) 5,6
E4) -20
E5) dV = 25,6 cm3
E6) dA = 0,002 3 cm2
E7) . dV = 60cm3
0,9 cm3
E8) dV =
E9) a) 2,17
b) 2,99
c) 5,92
E10) dz = 12x2y2dx + 8x3ydy
E11) df(4,3) =
2
3
dx
dy
5
10
E12) dV = 2,8 cm3
E13) a)
z = - 0,0804 , dz = - 0,08
b) z = 0,3899 , dz = 0,38
E14) dA = - 0,25 cm2
E15) dV = 3,12 cm3 ,
E16) dV = 3,2
V = 3,19728 cm3
cm3
E17) dD = -0,154 cm
E18) dV = 2,85 cm3
E19) a) dC = R$ 10,17
b)
C = R$ 10,47
E20) 1,003
29
e) 2,00

34. 4. ANÁLISE DO COMPORTAMENTO DE UMA FUNÇÃO
Considere o gráfico abaixo, de uma função polinomial f.
y
f
20
10
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
x
-10
-20
a) A função f é crescente em (
, 0]  [15,25]  [40,
).
b) A função f é decrescente em [0,15]  [25,40].
Observações:
a) Os intervalos onde f é crescente ou decrescente são partes do domínio da f.
b) Os pontos onde f muda o crescimento apresentam retas tangentes ao gráfico de f horizontais.
c) Retas horizontais tem declividade “zero”, portanto f’(0) = f’(15) = f’(25) = f’(40) = 0.
d) A função f não possui máximo, pois não existe o ponto mais alto do gráfico.
e) A função f não possui mínimo, pois não existe o ponto baixo do gráfico.
f) A função f possui máximos, por exemplo, nos intervalos (-5,5) e (20,30). Este tipo de máximo é
denominado máximo local ou relativo.
g) A função f possui mínimos, por exemplo, nos intervalos (10,20) e (35,45). Este tipo de mínimo é
denominado mínimo local ou relativo.
h) Os máximos relativos de f são 20 e 10, que acontecem, respectivamente, nos pontos 0 e 25.
i) Os mínimos relativos de f são -10 e -20, que acontecem, respectivamente, nos pontos 15 e 40.
j) Os máximos e mínimos relativos de f são denominados extremos relativos de f.
30

35. 4.1. PONTO CRÍTICO
Um ponto c do domínio de uma função f é chamado de ponto crítico de f se f ’(c) = 0, ou f ’(c) não existe.
Geometricamente:
y
y
y
t
0
c
y
t
x
0
y
c
t
x
y
0
y
c
t
x
c
y
t
0
x
t
t
0
c
x
0
c
x
0
c
x
0
c
x
E1) Encontre os pontos críticos de f, sendo:
1)f(x)=x3 – 3x + 2
3) f(x)= 5 x 3
2) f(x)=x4– 2x2 + 3
4) f(x)=
3
x2
4
4.2. FUNÇÃO CRESCENTE E FUNÇÃO DECRESCENTE
Uma função f é dita crescente num intervalo I, se a medida que x cresce, o valor de f(x) também cresce.
Uma função f é dita decrescente num intervalo I, se a medida que x cresce, o valor de f(x) decresce.
4.3. DETERMINAÇÃO DOS INTERVALOS DE CRESCIMENTO E
DECRESCIMENTO
Seja f uma função continua em [a,b] e derivável em (a,b).
a) Se f ’(x)>0 para todo x
b) Se f ’(x)< 0 para todo x
(a,b) então f é crescente em [a,b]
(a,b) então f é decrescente em [a,b]
Exemplo:
Determine os intervalos de crescimento e decrescimento da função dada por f(x) = x 3 – 6x2 + 1.
31

36. Solução:
1o) Determinação dos pontos críticos:
f’(x) = 3x2 – 12x
3x2 – 12x = 0
3x.(x – 4) = 0
2o) Determinação do sinal da derivada nos intervalos (
Para qualquer x (
3x = 0 ou x – 4 = 0
,0) , (0,4) e (4,+
,0) , f’(x) > 0, logo f é crescente em (
C={0,4}
):
,0).
Para qualquer x (0,4) , f’(x) < 0, logo f é decrescente em (0,4).
Para qualquer x (4, +
) , f’(x) > 0, logo f é crescente em (4, +
).
Importante:
Para determinar o sinal da derivada num intervalo, basta escolher um ponto qualquer do intervalo e
calcular a derivada nesse ponto.
E2)Determine os intervalos de crescimento e decrescimento das funções dadas por:
1) f(x)=x3 –5
2) f(x)=x4– 8x2 – 5
4) f(x)= x 4– 4x3
3) f(x)= 2x – 1
4.4. DETERMINAÇÃO DOS EXTREMOS RELATIVOS DE UMA FUNÇÃO
4.4.1. TESTE DA DERIVADA PRIMEIRA(TDP)
Seja f uma função continua e derivável em (a,b), exceto possivelmente em c
(a,b)
a) Se f ’ passa de positiva para negativa em c então f(c) é máximo relativo de f
b) Se f ’ passa de negativa para positiva em c então f(c) é mínimo relativo de f
c) Se f ’ não muda de sinal em c então f(c) não é extremo relativo de f
Geometricamente:
y
y
y
t
0
c1
y
t
x
0
c2
t
x
0
c1 é ponto de máximo relativo e f(c1) é máximo relativo de f
c2 é ponto de mínimo relativo e f(c2) é mínimo relativo de f
c3 e c4 não são pontos extremantes
32
c3
t
x
0
c4
x

37. Exemplo:
Determine os máximos e os mínimos relativos da função dada por f(x) = x 4 – 8x2 .
Solução:
1o) Determinação dos pontos críticos:
f’(x) = 4x3 – 16x
4x3 – 16x = 0
4x.(x2 – 4) = 0
2o) Determinação do sinal da derivada nos intervalos (
4x = 0 ou x2 – 4 = 0
,-2) , (-2,0) , (0,2) e (2,+
,-2) , f’(x) < 0, logo f é decrescente em (
Para qualquer x (
C={-2,0,2}
):
,-2).
Para qualquer x (-2,0) , f’(x) > 0, logo f é crescente em (-2,0).
Para qualquer x (0,2) , f’(x) < 0, logo f é decrescente em (0,2).
Para qualquer x (2, +
) , f’(x) > 0, logo f é crescente em (2, +
).
TDP
f(-2) = -16 é mínimo relativo de f, f(0) =0 é máximo relativo de f e f(2) = -16 é mínimo relativo de f.
E3) Encontre os máximos e mínimos relativos das funções dadas por:
1) f(x)= x4 – 8x2 + 1
2) f(x)= x3 + 3x2 – 5
3) f(x) = 3x4 + 4x3 – 12x2 + 16
4) f(x) = x3 – 12x
4.4.2. TESTE DA DERIVADA SEGUNDA(TDS)
(a,b), tal que f ’(c)= 0.
Seja f uma função derivável em (a,b) e c
a) Se f ’’(c) > 0 então f(c) é mínimo relativo de f.
b) Se f ’’(c) < 0 então f(c) é máximo relativo de f.
c) Se f ’’(c) = 0, nada podemos concluir.
Exemplo:
Determine os máximos e os mínimos relativos da função dada por f(x) = x 4 – 8x2 .
Solução:
1o) Determinação dos pontos críticos:
f’(x) = 4x3 – 16x
4x3 – 16x = 0
4x.(x2 – 4) = 0
33
4x = 0 ou x2 – 4 = 0
C={-2,0,2}

38. 2o) Determinação da derivada segunda:
f’’(x) = 12x2 – 16
TDS
f’’(-2) = 32 > 0 então f(-2) = -16 é mínimo relativo de f
f’’(0) = -16 < 0 então f(0) =0 é máximo relativo de f
f’’(2) = 32 > 0 então f(2) = -16 é mínimo relativo de f
E4) Encontre os máximos e mínimos relativos das funções dadas por:
1) f(x)= x3–12x+4
2) f(x)=x3– 3x2+5
3) f(x)= x4 – 8x2 + 6
4) f(x)= 3x5– 5x3
4.5. CONCAVIDADE E INFLEXÃO
4.5.1. TESTE DA CONCAVIDADE
Se f ’’(x) existe em um intervalo (a,b) então o gráfico de f é
a) côncavo para baixo (CPB) se f ’’(x) < 0,
b) côncavo para cima (CPC) se f ’’(x) > 0,
x (a, b).
x (a, b).
4.5.2. PONTO DE INFLEXÃO
Um ponto c pertencente ao domínio da f é um ponto de inflexão de f se o gráfico de f muda a
concavidade em c. Neste caso, (c,f(c)) é um ponto de inflexão do gráfico de f.
Exemplo:
Determine os intervalos de CPC, os intervalos de CPB e os pontos de inflexão da função dada por
f(x) = x3 – 6x2 + 1.
Solução:
1o) Determinação dos pontos críticos da f’:
f’(x) = 3x2 – 12x
f’’(x) = 6x – 12
6x – 12 = 0
2o) Determinação do sinal da derivada segunda nos intervalos (
Para qualquer x (
Para qualquer x (2, +
x=2
C’={2}
,2) e (2,+
,2) , f’’(x) < 0, logo o gráfico de f é CPB em (
) , f’(x) > 0, logo o gráfico de f é CPC em (2, +
34
):
,2).
).

39. Importante:
Para determinar o sinal da derivada segunda num intervalo, basta escolher um ponto qualquer do intervalo
e calcular a derivada segunda nesse ponto.
E5) Encontre os intervalos de CPC e CPB das funções dadas por:
1) f(x)= x3–3x
2) f(x) = 2x4– 12x2
3) f(x)= 3x4 – 12x3 + 26
4) f(x)=x3+ 3x2 – 9x–5
E6) Faça um estudo completo do comportamento das funções abaixo.
1)f(x)= 3x4 – 8x3+ 6x2
2) f(x)=2x3 – 3x2 – 12x + 10
4) f(x) = x2 – 4x + 6
x3
3
2x 2
5) f(x) = x3 – 6x2+ 12x – 4
3) f(x) =
3x 10
E7) Deseja-se cercar um terreno retangular de área 60 m2, de modo que o custo para cercar as laterais seja
R$ 300,00 por metro linear e o custo para cercar a frente e o fundo seja de R$ 500,00 por metro linear.
Determine as dimensões do terreno de modo que o custo para cercá-lo seja o menor possível. Neste
caso, qual o custo mínimo?
E8) Por várias semanas, o serviço de transito vem pesquisando a velocidade do tráfego numa auto-estrada.
Verificou-se que, num dia normal de semana, à tarde, entre 1 e 6 horas a velocidade do tráfego é de,
aproximadamente v(t) = 2t3–21t2 + 60t + 40 km/h, onde t é o número de horas transcorridas após o
meio-dia. A que horas, dentro do intervalo de tempo mencionado, o tráfego se move mais rapidamente
e a que horas se move mais lentamente ?
E9) De uma folha laminada quadrada de 2 dm de lado, foram cortados quadrados iguais nos quatro cantos e
com o restante da folha foi construída uma caixa sem tampa. Determine as dimensões do quadrado
retirado para que o volume da caixa seja máximo.
E10) Seja P = – x3 + 300x a função que dá a quantidade produzida de certo produto agrícola em função
da quantidade de fertilizante.
1) Determine a quantidade de fertilizante necessária para que se tenha a produção máxima.
2) Determine os intervalos de CPC e CPB do gráfico da função Produção.
3) Faça um esboço do gráfico de P, observando os resultados obtidos nos ítens anteriores
35

40. E11) Seja R(q) = – q3 + 15q2 , a função Receita.
1) Para que valores de q a função Receita tem sentido ?
2) Encontre os intervalos de crescimento e decrescimento da função Receita.
3) Determine, se houver, os intervalos de CPC e CPB.
4) Qual é a receita máxima e a receita mínima ?
5)Faça o gráfico da função, assinalando os resultados obtidos no itens anteriores.
6) Determine a Receita Marginal para q = 5 e interprete o resultado obtido.
E12) Se L(x)= –x2 + 6x – 5 é a função lucro na venda de x unidades de um certo produto, determine o lucro
máximo.
E13) Seja C(x) = x3 – 6x2 +100x a função custo total para produzir x unidades de um certo produto.
Determine:
1) o Custo Marginal
2) o Custo Médio
3) o Custo Médio Marginal
4) o Custo Médio Mínimo
4.6. TAXA DE VARIAÇÃO DE UMA TAXA DE VARIAÇÃO
Podemos ouvir de um economista que, embora a taxa de inflação esteja crescendo, a taxa segundo a
qual ela cresce está decrescendo. Isto significa que os preços ainda continuam a subir, mas não tão
rapidamente quanto antes. Observe os gráficos abaixo:
y
f
y
f
0 a
c
b
x
0
a
c
b
x
No primeiro gráfico observa-se que:
a) em (a,c), f é crescente (y ’ > 0) e y ’’ > 0 (f ’ é crescente), portanto f cresce a taxas crescentes.
b) em (c,b), f é crescente (y ’ > 0) e y ’’ < 0(f ’ é decrescente), portanto f cresce a taxas decrescentes.
No segundo gráfico observa-se que:
a) em (a,c), f é decrescente (y ’ < 0) e y ’’ < 0 (f ’ é decrescente), portanto f decresce a taxas decrescentes.
b) em (c,b), f é decrescente (y ’ < 0) e y ’’ > 0 (f ’ é crescente), portanto f decresce a taxas crescentes.
36

41. E14) Aumentando seu gasto x com propaganda(em milhares de reais), uma empresa constata que pode
aumentar as vendas y (em milhares de reais) de um produto de acordo com o modelo
y
1
(300x 2
10.000
x 3 ),
0
x
200.
Ache o ponto de diminuição de resultados para este produto(ponto de retorno decrescente).
E15) Um índice de preços ao consumidor(IPC) é descrito pela função
I = – 0,2t3 + 3t2 + 100,
0
t
9
onde t = 0 corresponde ao ano de 1991. Encontre o ponto de inflexão da função I e discuta o
seu significado.
4.7. WINPLOT
O winplot é um programa para plotagem de gráficos de funções de uma e duas variáveis, extremamente
simples de ser utilizado pois dispensa o conhecimento de qualquer linguagem de programação e é distribuído
gratuitamente, podendo ser baixada da internet pelo site baixaki.ig.com.br/download/WinPlot.htm ou da
página do professor com manual.
37

42. 4.8. SITES RELACIONADOS
http://pt.wikibooks.org/wiki/C%C3%A1lculo_I/%C3%8Dndice/Aplica%C3%A7%C3%B5es_
das_derivadas
http://www.cepa.if.usp.br/e-calculo/
http://www.ufpi.br/uapi/conteudo/disciplinas/matematica/download/unidade5.pdf
http://www.exatec.unisinos.br/~kessler/arquivos/edirigido.doc
http://www.google.com.br/search?sourceid=navclient&ie=UTF8&rlz=1T4SUNA_enBR239BR240&q=aplica%c3%a7%c3%b5es+de+derivadas+na+adminis
tra%c3%a7%c3%a3o
http://www.scribd.com/doc/271621/Apostila-de-limites-e-derivadas
http://www.vestibular1.com.br/revisao/revisao_matematica_III.pdf
4.9. RESPOSTAS
E1) 1) –1 ; 1
2) –1 ; 0 ; 1
E2) 1) Cresc.
2) Cresc.:[-2,0]
3) Cresc.
4) Cresc.: [3,
E3) 1) Máx. Relativo: f(0) = 1
3) –3
[2,
) , Decresc.: (
) , Decresc.: (
4) –2 ; 0 ; 2
, 2]
,3]
Mín. relativo : f(–2) = f(2) = –15
2) Máx. Relativo: f(–2) = –1
Mín. relativo : f(0) = –5
3) Máx. Relativo: f(0) = 16
Mín. relativo : f(-2) = -16 e f(1) = 11
4) Máx. Relativo: f(–2) = 16
Mín. relativo : f(2) = –16
E4) 1) Máx. Relativo: f(–2) = 20
Mín. relativo : f(2) = –12
2) Máx. Relativo: f(0) = 5
Mín. relativo : f(2) =1
3) Máx. Relativo: f(0) = 6
Mín. relativo : f(–2) = f(2) = –10
4) Máx. Relativo: f(–1) = 2
Mín. relativo : f(1) = –2
38
[0,2]

43. E5) 1) CPB: (
,0) , CPC: (0,
3) CPB: (0,2) ,
E6) 1) Cresc.: [0,
CPC: (
2) Cresc.: (
CPB: (
3) Cresc.: (
CPB: (
4) Cresc.: (
CPC: (
2) CPB: ( 1,1) ,
)
,0)
(2,
)
4) CPB: (
CPC: (
, 1)
, 1) , CPC: ( 1,
(1,
)
)
1
,0] , Máx. Relativo: NE , Mín. relativo : f(0) = 0 , CPB: ( ,1) ,
3
1
e1
) , PI :
3
) , Decresc.: (
1
, )
3
(1,
) , Decresc.:[-1,2] , Máx. Relativo: f(–1) = 17 , Mín. relativo : f(2) = –10 ,
, 1] [2,
1
1
, ) , CPC: ( ,
2
2
,1] [3,
) , PI :
1
2
) , Decresc.:[ –1,3] , Máx. Relativo: f(1) =
,2) , CPC: (2,
34
, Mín. relativo : f(3) = 10 ,
3
) , PI : 2
,2] , Decresc.: [2,
) , Máx. Relativo:NE , Mín. relativo : f(2) = 2 , CPC: (
,
),
PI : NE
5) Cresc.: (
,
) , Máx. Relativo: NE , Mín. relativo : NE , CPB: (
,2) , CPC: (2,
) , PI : 2
E7) 10 m, 6 m e R$ 12000,00
E8) 2. horas e 5 horas
E9)
1
dm
3
E10) 1) x = 10
2) CPB: [0,10 3 ]
E11) 1) [0,15]
2) C: [0,10] , D: [10,15]
4) Rmáx = 500 , Rmín = 0
3) CPC: [0,5] , CPB: [5,15]
6) 75
E12) 1) Lmáx = 4
E13) 1) Cmg = 3x2 – 12x + 100
2) Cme = x2 – 6x + 100
E14) 100
E15) 5
39
3) Ç'me = 2x – 6
4) 91

44. 5. MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS
VARIÁVEIS
Seja z = f(x,y) uma função de duas variáveis. Dizemos que um ponto (x o,yo) do domínio de f é ponto de
máximo relativo ou local de f, se existir uma bola aberta de centro em (xo,yo) e raio r tal que, para todo ponto
P(x,y) do domínio situado no interior dessa bola, tenhamos f(x,y)
f(xo,yo).
O número f(xo,yo) recebe o nome de máximo relativo ou local de f. Exemplos: Figuras 2 e 3
Seja z = f(x,y) uma função de duas variáveis. Dizemos que um ponto (x o,yo) do domínio de f é ponto de
mínimo relativo ou local de f, se existir uma bola aberta de centro em (xo,yo) e raio r tal que, para todo ponto
P(x,y) do domínio situado no interior dessa bola, tenhamos f(x,y)
f(xo,yo).
O número f(xo,yo) recebe o nome de mínimo relativo ou local de f. Exemplos: Figuras 1 e 3
Figura 1
Figura 2
Figura 3
Figura 4
Seja z = f(x,y) uma função de duas variáveis. Dizemos que um ponto (xo,yo) do domínio de f é ponto de
máximo absoluto ou global de f, se para todo ponto P(x,y) do domínio, tivermos f(x,y)
f(xo,yo).
O número f(xo,yo) recebe o nome de máximo absoluto ou global de f. Exemplo: Figura 2
40

45. Seja z = f(x,y) uma função de duas variáveis. Dizemos que um ponto (x o,yo) do domínio de f é ponto de
mínimo absoluto ou global de f, se para todo ponto P(x,y) do domínio, tivermos f(x,y)
f(xo,yo).
O número f(xo,yo) recebe o nome de mínimo absoluto ou global de f. Exemplo: Figura 1
5.1. PONTO CRÍTICO DE UMA FUNÇÃO DE DUAS VARIÁVEIS
2
Seja z = f(x,y) uma função definida num conjunto aberto D
. Um ponto (xo,yo) D é um ponto crítico
de f se as derivadas parciais fx(xo,yo) e fy(xo,yo) são nulas(extremos suaves) ou não existem(extremos bruscos).
Geometricamente, são pontos do gráfico da função onde o plano tangente é horizontal ou não existe.
Exemplo:
x2
y2 1 .
1 2
(x
2
y2 )
Encontre os pontos críticos da função dada por f(x,y) =
Solução:
fx =
1 2
(x
2
x
1/ 2
x
2x
x
x
fx
fy
y2 )
2
y
fy =
2
1/ 2
y
2y
x
2
y2
0
y2
y
x2
2
se x = 0 e y = 0, fx e fy não existem, logo o ponto (0,0) é o ponto crítico de f.
0
y2
O gráfico da f é a superfície abaixo.
z
y
x
E1) Encontre os pontos críticos das funções:
1) f(x,y) = x2 + y2
2) f(x,y) = x3 + y3 – 3x2 – 3y
41
3)f(x,y) = 4x – 2y + 4

46. 5.2. CRITÉRIO PARA CARACTERIZAÇÃO DE PONTOS EXTREMANTES
TESTE DO HESSIANO
Seja z = f(x,y) uma função continua, com derivadas parciais até segunda ordem continuas e (x o,yo) um
ponto crítico de f, tal que fx(xo,yo) = fy(xo,yo) = 0.
a)Se H(xo,yo) > 0 e fxx(xo,yo) > 0 então (xo,yo) é ponto de mínimo relativo de f.
b) Se H(xo,yo) > 0 e fxx(xo,yo) < 0 então (xo,yo) é ponto de máximo relativo de f.
c) Se H(xo,yo) < 0 então (xo,yo) não e ponto extremante, é ponto de sela.
d) Se H(xo,yo) = 0, nada se pode afirmar.
Exemplo:
Determine e caracterize os pontos extremantes da função f(x,y) = –3x2 – y2 + xy – 5.
Solução
a) Determinação dos pontos críticos da função:
6x y 0 (1)
fx = –6x + y
fy = –2y + x
isolando y na equação (1), vem:
2 y x 0 (2)
y = 6x. Substituindo na equação (2), y por 6x, vem: – 2.6x + x = 0
–12x + x = 0
–11x = 0
x = 0. Como y = 6x e x = 0
y = 0.
Logo, o ponto crítico de f é (0,0).
b) Determinação do Hessiano de L:
fx = –6x + y
fxx = –6 e fxy = 1
H(x,y) =
fy = –2y + x
6
1
1
fyy = –2 e fyx = 1
2
c) Caracterização do ponto crítico:
H(0,0) =
6
1
1
2
= 12 – 1 = 11> 0, logo (0,0) é ponto extremante(de máximo ou de mínimo).
Como fxx(0,0) = –6 < 0, o ponto (0,0) é ponto de máximo.
42

47. E2) Determine e caracterize os pontos extremantes das funções:
1)f(x,y) = 3x4 + 8x3 – 18x2 + 6y2 + 12y – 4
2) f(x,y) = x2 + y2 – 2x + 1
3) f(x,y) = x3 + 3xy + y2 – 2
4) f(x,y) = 8x 3 – 3x2 + y2 + 2xy + 2
5) f(x,y) = x3 + y2 – 6xy + 6
6) f(x,y) = x3 + 2y2 – 3x – 4y – 8
7) f(x,y) = –x2 – y3 + 4x + 3y
8) f(x,y) =
8x 3
3
2xy 3x 2
y2 1
E3) A função lucro de uma loja foi determinada como sendo L(x,y) = – x3– x2 – y2 + 2xy + 3x + 10, onde x e
y são as quantidades de dois produtos negociados . Quais os valores de x e y que maximizam o lucro ?
E4) Sejam px = 27 – x2 e py = 12 – y2 as funções Demanda para dois produtos de quantidades x e y. Determine
a receita máxima.
E5) Seja z = 10 – 2x2 + xy – y2 + 5y uma função Produção, onde x e y são quantidades de dois insumos
utilizados na fabricação da quantidade z de um produto. O preço unitário de cada insumo é 3, e o
produto acabado é vendido por 6. Calcule o lucro máximo.
5.3. MÁXIMOS E MÍNIMOS CONDICIONADOS
Seja z = f(x,y) a função da qual se quer determinar o máximo ou mínimo sujeito à condição R(x,y) = 0.
z
z
máx de f sem restrição
máx de f com restrição
0
y
0
x
x
43
restrição R
y

48. 5.3.1. MÉTODO DA SUBSTITUIÇÃO
Consiste em substituir x (ou y) obtido a partir da restrição R(x,y) = 0, na função f. Obtém-se dessa forma
uma função de uma só variável, e o problema se reduz à determinação de máximos e mínimos da função
de uma variável.
Exemplo:
Sejam z = xy e C = 2x + y + 6 as funções Produção e Custo associadas para um determinado produto,
Onde x e y são quantidades de dois insumos e z é a quantidade do produto acabado. Determine o custo
mínimo para a produção de 50 unidades.
Solução:
1o) Identificação da função e restrição:
Queremos o custo mínimo para a produção de 50 unidades, logo a função que deve ser otimizada é a custo
C = 2x + y + 6.
Queremos que a produção seja de 50 unidades, logo a restrição é z = 50 ou R(x,y) = xy – 50 = 0.
2o) Aplicação do Método da Substituição:
Podemos isolar x ou y na restrição, seja y =
função de variável x : F(x) = 2x +
50
50
. Substituindo na função Custo, y por
, obtemos uma
x
x
50
+ 6 e, portanto, recaímos num problema de máximos e mínimos de
x
funções de uma variável, que pode ser resolvido pelo Teste da derivada primeira(TDP) ou pelo teste da
derivada segunda(TDS).
a) Determinação dos pontos críticos de F:
50
50
50
F’(x) = 2
2
=0
2=
2
2
x
x
x2
x2 = 25
x = 5 ou x = – 5(não tem sentido, neste caso).
b) TDS:
F’(x) = 2
50
F’’(x) =
100
3
. Como
F’’(5) =
100
> 0 , o ponto 5 é ponto de mínimo da F e,
x
x
53
50
como y =
, o ponto (5,10) é ponto de mínimo da função custo C sujeita à restrição R.
x
2
Conclusão: o custo mínimo para a produção de 50 unidades é C(5,10)= 26.
44

49. 5.3.2. MÉTODO DOS MULTIPLICADORES DE LAGRANGE
Consiste em construir a função de Lagrange L(x,y,
L
0
x
L
0
y
R ( x , y)
) = f(x,y) - R(x,y) e resolver o sistema
0
Os possíveis pontos extremantes de f sujeita à restrição R(x,y) = 0 são os pontos (x 0 ,y0) tais que (x0 ,y0, )
são soluções do referido sistema.
Exemplo:
Sejam z = xy e C = 2x + y + 6 as funções Produção e Custo associadas para um determinado produto, onde
x e y são quantidades de dois insumos e z é a quantidade do produto acabado. Determine o custo mínimo
para a produção de 50 unidades.
Solução:
Este é o mesmo exercício do exemplo anterior, isto é: Mín C s. à R(x,y) = xy – 50 = 0.
Vamos resolvê-lo pelo Método dos multiplicadores de Lagrange.
1o) Construção da função de Lagrange: L(x,y, λ ) = 2x + y + 6 – λ (xy – 50 ) =2x + y + 6 – λ xy + 50 λ
2o) Cálculo das derivadas parciais de L: Lx = 2 – λ y
Ly = 1 – λ x
3o) Resolução do sistema formado por Lx = 0, Ly = 0 e R(x,y) = 0:
2 λy
0
1 λx 0
xy 50 0
isolando λ nas duas primeiras equações, vem: λ =
Substituindo y por 2x na restrição, temos: x.2x – 50 = 0
sentido, neste caso). Como y = 2x e x = 5
2
y
2x2 = 50
1
x
y = 2x.
x2 = 25
x = 5 ou x = – 5(não tem
y = 10.
Então o ponto (5,10) é ponto de mínimo da função custo C sujeita à restrição R, isto é, o custo mínimo para a
produção de 50 unidades é C(5,10)= 26.
45

50. E6) Seja L(x,y) = – 2x2 – y2 + 32x + 20y a função lucro de uma indústria que produz e comercializa dois
produtos em quantidades x e y. Calcular o lucro máximo, sabendo que a produção da indústria é limitada
em 24 unidades.
E7) Deseja-se cercar um terreno retangular de área 60 m2, de modo que o custo para cercar as laterais seja
R$ 300,00 por metro linear e o custo para cercar a frente e o fundo seja de R$ 500,00 por metro linear.
Determine as dimensões do terreno de tal modo que o custo para cercá-lo seja o menor possível. Nesse
caso, qual o custo mínimo para cercá-lo ?
E8) Ache o ponto de máximo ou de mínimo das funções a seguir:
1)f(x,y) = x2 + y2 , sujeito a x + y – 4 = 0
2)f(x,y) = 2x + y – 10 , sujeito a xy = 200
3)f(x,y) = 9 – x2 – y2 , sujeito a x + y – 2 = 0
4) f(x,y) = x 1 / 2 y1 / 2 , sujeito a 2x + 10y = 60
E9) Suponha que a função Produção para uma empresa é z = 10x 1 / 2 y1 / 2 e que a função Custo associada é
C = 2x + 2y + 10. Suponha, ainda, que o fabricante limita seu custo em 46 e decida em que ponto se
tem a produção máxima com o custo fixado em 46.
E10)Sabendo que U(x,y)=xy é a função índice de utilidade de um consumidor e que sua restrição orçamentária
é 2x+3y =36, determine as quantidades x e y que maximizam U.
E11)Seja z = xy a função Produção de uma empresa que utiliza dois insumos em quantidades x e y. Se os
Preços unitários dos insumos são px = 2 e py = 3 , o custo fixo de produção é 5 e o produto acabado é
vendido por 6, determine o lucro máximo que se pode atingir com um custo de 77.
5.4. SITES RELACIONADOS
http://www.eqm.unisul.br/disciplinas/calcIII/4-Maximos%20e%20m%C3%ADnimos.pdf
http://www.pucrs.br/famat/demat/eng/calculo_I/files/material_apoio/extremos2.pdf
http://miltonborba.org/CDI2/Func_vv.pdf
http://docentes.fe.unl.pt/~mdsoares/caderno6.pdf
http://www.ppge.ufrgs.br/sergio/oferta.pps#265
http://www.ppge.ufrgs.br/sergio/demanda.pps#264
46

51. 5.5. RESPOSTAS
2) (0, –1) , (0,1), (2, –1) e (2,1)
E1) 1) (0,0)
3) Não tem
E2) 1) (0, –1) é ponto de sela , (1, –1) e (–3, –1) são pontos de mínimo
2) (1,0) é ponto de mínimo
3 9
3) (0,0) é ponto de sela; ( , ) é ponto de mínimo
2 4
1 1
4) (0,0) é ponto de sela; ( , ) é ponto de mínimo
3 3
5) (0,0) é ponto de sela ; (6,18) é ponto de mínimo
6) (–1,1) é ponto de sela ; (1,1) é ponto de mínimo
7) (2,-1) é ponto de sela; (2,1) é ponto de máximo
8) (0,0) é ponto de sela; (1, –1) é ponto de mínimo
E3) (1,1)
E4) 70
E5) Lmáx = L(1/2,5/2) = 93
E6) 204
E7) 10 m, 6 m e R$ 12000,00
E8) 1) (2,2)
2) (10,20) e (-10,-20)
3) (1,1)
E9) (9,9)
E10) (9,6)
E11) 1219
47
4) (15,3)

52. 6. INTEGRAL INDEFINIDA
Em matemática, cada vez que definimos uma operação, pensamos na sua operação inversa, que desfaz o efeito
da primeira. Assim, a subtração é a operação inversa da adição, a divisão é a operação inversa da multiplicação
e a extração da raiz quadrada é a inversa da operação que eleva ao quadrado. Estamos agora interessados na
operação inversa da derivação.
DERIVAÇÃO
F
F’= f
PRIMITIVAÇÃO
6.1. PRIMITIVA
Uma função F é chamada de primitiva de uma função f em um intervalo I se F’(x) = f(x),
x
I.
Exemplos:
As funções dadas por F1(x) = x2, F2 (x) = x2 + 1, F3(x) = x2 – 1 são primitivas da função dada por f(x) = 2x.
A função f possui infinitas primitivas que podem ser representadas por F(x) + k chamada de primitiva
geral ou integral indefinida da f que é notada por
f(x)dx ou seja f(x)dx = F(x) + k.
6.2. INTERPRETAÇÃO GEOMÉTRICA DA INTEGRAL INDEFINIDA
A integral indefinida de uma função f é representada geometricamente por uma família de curvas que em
pontos de mesma abscissa possuem retas tangentes paralelas.
Exemplo: 2 xdx
x2
k
48

53. E1) Determine:
1) 2xdx
3) 3x 2 dx
2) 5dx
4)
(5x 4
3x 2 dx
dx
x3
3
dx
2
3
dx
2
4x 3 )dx
6.3. REGRAS DE INTEGRAÇÃO
[f(x)
1.
g(x)]dx
f(x)dx
g(x)dx
Exemplos:
a)
(e x 1)dx
2.
e x dx
cf(x)dx
dx
ex
x k
b)
(3x 2 1)dx
x k
c f(x)dx , sendo c uma constante
Exemplos:
a) 5.e x dx 5 e x dx 5e x k
3.
dx
4.
e x dx
5.
dx
x
x
b)
k
ex
k
ln | x | k
E2) Encontre:
1) 2dx
2)
(3 e x )dx
4) edx
5)
(ln2
8)
(3e e x )dx
7) (
2e ln 6)dx
3) (1
2
)dx
x
6) (
49
4
5
9) (
5e x )dx
2
)dx
3x
2x 3
)dx
x
3x
2
k

54. xp 1
k , sendo p
p 1
x p dx
6.
-1
Exemplos:
a)
b)
3
x4
4
x 3 dx
x 2 dx
dx
c)
x
k
x
x 4 dx
4
3
x5/3
5/3
x 2 / 3 dx
3
3
3 x5
5
k
1
k
k
k
3x 3
E3) Encontre:
1)
4)
3x 2 dx
2)
5)
dx
3x
2
(2x 4 - x 3
x dx
10)
x x dx
(
8)
5
2x
3
2
x
11)
)dx
4
Se u = f(x) , u p u ' dx
7.
2)dx
3)
6)
(x 5 - 2x 3
5x - 3)dx
dx
x
3
7)
3x 2 - x
x
dx
x
x3
9)
2x 1
dx
x2
up 1
k, se p
p 1
(
12) (
2
x
1
3x 2
1
Exemplos:
(2x - 4) 4
4
a)
(2x - 4) 3 .2dx
b)
(3x - 2) 4 dx , observe que u = 3x – 2 e u’ = 3 não aparece na integral.
(3x - 2) 4 dx
k , observe que u = 2x – 4 e u’ = 2
3
(3x - 2) 4 . dx
3
1
(3x - 2) 4 .3dx
3
1 (3x - 2) 5
.
3
5
50
k
(3x - 2) 5
15
k
3
x2
)dx
x )dx

55. (5x 3)1 / 2 dx , observe que u = 5x +3 e u’ = 5 não aparece na integral.
5x 3.dx
c)
5
(5x 3)1/2 . dx
5
(5x 3)1/2 dx
dx
d)
(2x 6)
1
(5x 3)1/2 .5dx
5
1 (5x 3) 3/2
.
5
3/2
k
2 (5x 3) 3
(2x 6) 3 dx , observe que u = 2x + 6 e u’ = 2 não aparece na integral.
3
2
(2x 6) -3 . dx
2
(2x 6) -3 dx
1
(2x 6) -3 .2dx
2
1 (2x 6) -2
.
2
-2
k
1
4(2x 6) 2
E4) Encontre:
(3x 1) 4 3dx
1)
8.
Se u = f(x) ,
2)
e u u ' dx
eu
(3x 1) 4 dx
3) (1 - x) 5 dx
k
Exemplos:
a)
e 2x- 4 .2dx
b)
e 3x - 2 dx , observe que u = 3x – 2 e u’ = 3 não aparece na integral.
e 2x- 4
dx
e
e
2x 6
e
2x 6
dx
dx
k , observe que u = 2x – 4 e u’ = 2
3
e 3x-2 . dx
3
e 3x-2 dx
c)
2x 6
1 3x-2
e
.3dx
3
1 3x
.e
3
2
k
dx , observe que u = 2x + 6 e u’ = 2 não aparece na integral.
e -2x-6 .
-2
dx
-2
1
e -2x-6 .(-2)dx
2
1
.e
2
2x 6
1
k
e
2x 6
k
E5) Encontre:
1)
e 4x 4dx
k
15
2)
e 4x dx
3) e -x dx
51
k

56. 9.
Se u = f(x) ,
u ' dx
u
ln | u | + k
Exemplos:
a)
2dx
2x - 4
b)
dx
, observe que u = 3x – 2 e u’ = 3 não aparece no numerador.
3x - 2
ln | 2x 4 | k , observe que u = 2x – 4 e u’ = 2 aparece no numerador.
dx
3x - 2
3 dx
.
3 3x - 2
1 3dx
3 3x - 2
1
ln | 3x 2 | k
3
E6) Encontre:
2x
1)
x
2
dx
3
x
2)
x
2
3)
dx
3
1
dx
5x 2
(3 x 2
4) 5 xdx
E7) Encontre:
1) (2x 1) 3 2dx
xdx
4)
5 x
7)
16)
5)
2
3
3 x2
2dx
e
x 1
20xdx
2
dx
3)
(x
dx
9)
2x 1
3
10
x
2
dx
xdx
6)
4
11)
e 3x 1dx
12)
14)
3e x
x
8)
5
2x
x 2 1. 2xdx
(1 x )
xdx
10)
13)
2)
dx
4x 2
15)
17)
5e 2 dx
x
18)
52
2
2) 3
dx
(2x 3) 5
x 2 dx
x3 1
3xe x
dx
ex
2 3
dx

57. E8) Determine a equação da curva y = f(x) que passa pelo ponto P, sabendo que:
1) P(2,1) e f ’(x)= 2x
2) P(1,5) e f ’(x)= 6x 2 – 2x + 5
4) P(0,-2) e f ’(x) = ex – 2
5) P(1,5) e f ’(x) =
3) P(–2, –3) e f ’(x) = 3x2 + x – 1
2
x
E9) Dadas as funções Cmg = 22q e Rmg = 3q2 + 6q + 2, respectivamente Custo Marginal e Receita Marginal
para um determinado produto, determine as funções Custo, Receita e Lucro, sabendo que o custo de
duas unidades é 84.
E10) Dadas as funções Rmg = –4q3 + 64q, Cmg = 20 e Cf = 200, respectivamente Receita Marginal, Custo
Marginal e Custo Fixo para um mesmo produto, determine a função Lucro.
Importante: A taxa de variação de f(x) em relação a x é o mesmo que a derivada de f(x) em relação a x.
E11) O preço de uma máquina desvaloriza-se a uma taxa de –20x mil reais ao ano . Se a máquina durou
quatro anos e seu valor residual foi R$ 40.000,00, qual foi seu preço inicial ?
E12) O preço de uma mercadoria, que atualmente custa R$ 1.000, varia, com a inflação, a uma taxa de 40x
reais ao mês. Quantos custará daqui a cinco
meses ?
E13) Uma indústria que tem 225 operários produz 750 unidades de certo produto. A taxa de variação da
produção em relação ao número de operários é dada por
25
. Qual será a produção da fábrica, se
x
forem admitidos mais 31 funcionários ?
E14) Uma empresa estima que o crescimento de sua renda mensal, em milhões, em função do tempo, em
meses, será à taxa de 3(t + 4)-1/2, a partir de hoje. Sabendo que a renda atual da empresa é de 12
milhões, calcule a renda daqui a um ano.
E15) Daqui a x anos, a população de certo país variará a uma taxa estimada de e0,1x milhões de
habitantes por ano. Se a população atual é de 120 milhões de habitantes, qual a função P = f(x) que
dá a população em função do tempo? Qual será a população desse país daqui a 20 anos?
53

58. E16)Um certo bem desvaloriza-se a uma taxa de –10x reais ao ano. Se o bem durou três anos e seu valor
residual foi R$ 105,00 ; qual foi seu preço inicial ?
E17) A função Produção Marginal de um produtor, em relação a um insumo de quantidade x , é dada por
Pmg = –2x + 8. Determine:
1) a produção marginal no ponto 2 e interprete o resultado;
2) a função Produção, sabendo que a quantidade produzida P é 25 quando a quantidade usada x de
insumo é 5;
E18) Sabendo que o custo marginal é dado por Cmg(x) = 10 e o custo de produção de duas unidades é
35 u.m., determine o custo fixo.
E19) A função Produção Marginal de um produtor, em relação a um insumo de quantidade x, é
Pmg = – 3x2 + 24x. Determine a função Produção, sabendo que a quantidade produzida P é 11 quando
a quantidade usada x de insumo é 1.
E20) Um fabricante pode produzir um determinado produto cujo preço de venda é R$ 20,00 a unidade. O
fabricante estima que se x unidades forem vendidas por semana, o custo marginal será Cmg=2x – 10.
Ache o lucro obtido pela produção e venda de 10 unidades desse produto, sabendo que o custo de
produção de quatro unidades é R$ 36.00.
E21)Um fabricante produz e vende uma quantidade q de certa mercadoria. As funções Custo Marginal
e Receita Marginal são respectivamente Cmg = 2q + 20 e Rmg = –2q + 140. Sabendo que o custo
de produção de dez unidades é R$ 800,00 , determine:
1) a função Lucro Total;
2) o lucro decorrente da venda de 5 unidades;
3) a variação do lucro decorrente da venda da 5a unidade;
4) a função Lucro Marginal;
5) o Lucro Marginal no ponto 4 e interprete o resultado obtido;
6) a equação da demanda.
54

59. 6.4. SITES RELACIONADOS
http://www.exatec.unisinos.br/~matematica/arquivos/intindef.doc
http://www.geocities.com/puc3ware/tutoria_de_matamatica.html#menu_de_assuntos
http://www.somatematica.com.br/superior/integrais/integrais.php
http://www.dm.ufscar.br/~sampaio/calculo1_aula15.pdf
http://wwwp.fc.unesp.br/~arbalbo/arquivos/integralindefinida.pdf
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm
http://pt.wikipedia.org/wiki/C%C3%A1lculo
http://www.pucrs.br/famat/marcia/arquitetura/Integral_indefinida.pdf
http://br.answers.yahoo.com/question/index?qid=20080223183956AAHLVc2
http://www.ufpi.br/uapi/conteudo/disciplinas/matematica/uni07_fun_pri_01.html
http://www.ufpi.br/uapi/conteudo/disciplinas/matematica/uni07_int_ind_01.html
http://www.hottopos.com.br/regeq8/cardoso2.htm
http://www.cepa.if.usp.br/e-calculo/integrais/primitivas/primitivas.htm
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm#int09
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm#int10
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm#int11
55

60. 6.5. RESPOSTAS
E1)1) x2 + k
2) 5x + k
3) x 3 + k
4) x5 + x4 + k
E2) 1) 2x + k
2) 3x + e x + k
3) x – 2ln |x| + k
4) ex + k
4x
5
6)
2
ln | x | k
3
E3) 1) x3 + k
2 x3
3
5)
k
5
2x
10)
E4) 1)
2)
E5) 1) e 4x
5)
3| k
1
ex
1
4
2)
1
ln | x 2
2
2)
k
2 x5
5
k
12)
3)
k
3)
3
1
10) 3e x
2) 2
3
x
k
k
k
k
k
k
3)
(3x 2 4) 6
36
k
7)
5
ln | x |
2
k
k
18)
ex
ex
2 x3
3
1
3x
(1 x ) 6
6
1
9) 2 ln | x |
k
1
3x
4)
3x k
1
ln | 5x 2 | k
5
3
x
k
56
k
4
11)
e 3x
3
8)
1
12)
k
2
k
4) – 5 x 2
k
33 (3 x 2 ) 2
3e x
15)
2
1
14) ln | 4x 2 | k
4
1
5x 2
2
9) 2x – 3ln |x| + k
3)
3| k
2 ( x 2 1) 3
x4
2
8) 33 x
k
4( x 2
x6
6
k
1
x
2 ln | x |
e 4x
4
x
17)10 e 2
x2
2
(3x 1) 5
15
6)
k
3(1 x ) 3
8(2x 3)
13)
k
1
2
7)
11)
3)
2x k
k
2)
(2x 1) 4
4
9)
x2
2
x3
2)
k
k
E6) 1) ln | x 2
E7) 1)
k
x3
(3x 1) 5
5
x4
4
6) 2 x
1
8)3ex + e x + k
7) ( – 2e + ln 6)x + k
2x 5
5
5) xln 2 – 5ex + k
k
2x 1 k
1
ln | x 3 1 | k
3
3
k
16)10ln(x2 +10) + k

61. E8) 1) y = x2 – 3
2) y = 2 x3 – x2 + 5x – 1
4) y = ex – 2x –3
3) y = x3 +
x2
– x +1
2
5) y = 2ln x + 5
E9) C = 11q2 + 40 ; R = q3 + 3q2 + 2q ; L = q3 – 8q2 + 2q – 40
E10) L = – q4 + 32q2 – 20q – 200
E11) V = 200.000
E12) R$ 1.500,00
E13) P(256) = 800
E14) R(12) = 24 milhões
E15) Aproximadamente 183,8 milhões de habitantes
E16) 150
E17) 1) Pmg(2) = 4
2) P = – x2 + 8x + 10
E18) 15
E19) P = – x3 + 12x2
E20) 140
E21) 1) L =–2q2 + 120q – 500
5) 104
2) 50
3) 102
6) q = –p + 140
57
4) Lmg = –4q + 120

62. 7. INTEGRAL DEFINIDA
Seja f uma função e F uma primitiva de f. A integral definida de f de a até b é o número real
representado por
b
a
f(x)dx e calculado por F(b) - F(a).
b
a
b
a
f(x)dx = [F(x)]
= F(b) - F(a)
Exemplos:
3
a)Calcule
x 2 dx
0
Solução:
1o ) Cálculo da integral indefinida:
x 2 dx
x3
3
k
2o ) Cálculo da integral definida:
3
0
3
9 0
9
0
4
1
b) Calcule
x3
x dx
3
2
(1 x) dx
1
Solução:
1o ) Cálculo da integral indefinida:
(1 x ) 4 dx
(1 x ) 4
1
dx
1
(1 x) 5
5
1 (1 x) 4 ( 1)dx
2o ) Cálculo da integral definida:
1
4
(1 x) dx =
1
(1 x ) 5
5
1
32
5
0
1
32
5
E1) Calcule:
3
1)
x 2 dx
0
2)
0
1
58
(1 2x) 4 dx
k

63. 7.1. PROPRIEDADES BÁSICAS
a)
b)
c)
d)
a
a
f(x)dx = 0
b
a
a
b
f(x)dx = -
f(x)dx
b
b
a
a
c.f(x)dx = c.
b
a
[f(x)
f(x)dx , sendo c uma constante
g(x)]dx =
b
b
f(x)dx ±
g(x)dx
a
a
e)
b
c
f(x)dx = f(x)dx +
a
a
f)
b
f(x)dx
a
0, se f(x)
b
c
0,
f(x)dx , com a < c < b
x
[a,b]
E2)Calcule:
1
1)
3)
5)
7)
9)
11)
0
(x 4
9
2)
dt
4)
t
1
t 1
2
2
2
1
t
1
4
3x 3 1)dx
t
dt
6)
(2x - 6) 4 dx
x2
2
1
(x
3
1
3
1)
x4
2
x3
x
8)
dx
10)
dx
59
0
1
(3x 5
3x 2
2x 1)dx
2 2
x (x - 1)dx
0
2
1
1
0
(2x - 4) 5 dx
8x(x 2 1) 3 dx
0
dx
-1
1- x

64. 7.2. INTERPRETAÇÃO GEOMÉTRICA DA INTEGRAL DEFINIDA
Seja f uma função continua em [a,b] com f(x)
x
0,
[a,b].
Vamos calcular a área da região situada entre o gráfico de f e o eixo das abscissas de a até b.
y
f
f(x+ Δx )
A1
A2
f(x)
A3
ΔA
A
0
a
x + Δx
x
b
x
A é a área da região hachurada, ΔA é o acréscimo que sofre a área A quando x recebe um acréscimo Δx .
A3
( A2 + A3 )
lim f(x)
lim
x
x
0
0
(A1 + A2 + A3 )
ΔA
Δx
lim f(x + Δx )
x
ΔA
f(x). Δx
f(x + Δx ). Δx
lim
f(x)
x
0
0
ΔA
Δx
f(x )
f(x)
lim
x
0
ΔA
Δx
ΔA
= f(x)
Δx
f(x + Δx )
A’ = f(x)
Então A é uma primitiva de f(x) , logo A = F(x) + k.
Para x = a, A = 0 e k = -F(a), logo A = F(x) - F(a)
Para calcular a área de a até b basta tomar x = b.
b
Para x = b, A = F(b) - F(a) =
f(x)dx
a
b
Se f é uma função continua e não negativa em [a,b], o número
f(x)dx representa a área da região
a
limitada pelo gráfico de f, pelo eixo Ox e pelas retas verticais x = a e x = b.
y
f
R
0
a
b
b
AR =
f(x)dx
a
60
x

65. 7.3. ÁREA DA REGIÃO ENTRE DUAS CURVAS
Sejam f e g funções continuas em [a,b] , com f(x)
x
g(x) ,
[a,b]. Se R é a região limitada pelos
b
gráficos de f, g, x=a e x=b então AR =
[f(x) - g(x)]dx
a
y
f
R
g
0
a
b
x
E3) Escreva a integral que fornece a área da região R:
1)
y
f
R
–4
2)
0
2
x
y
–1
0
R
6
x
f
3)
y
g
–2
3
0
x
R
f
4)
g
y
f
R
–3
3
0
5)
x
y
–2
4
0
x
g
R
f
61

66. E4)Use integração para calcular as áreas das regiões hachuradas.
a)
f(x) = x
b)
f(x) = -x2 + 4
f(x) = x 2 – 4
c)
d)
f (x)
x
2
2
62

67. e)
g(x) = x2
f(x) = x
f)
f x
x3
gx
-x 2
E5)Calcule a área da região limitada por:
1) y=–x2 + 4 e y=0
2) y=x 2 – 4, y=0, x=–1 e x=2
3) y=x, y=0, x=–2 e x=1
4) y=x2 – 1 e y=3
5) y=x2 + 1, y=2x – 2, x=–1 e x=2
6) y=x3, y=–x + 2 e y=0
7) y=
x
e y=x2
8) y=x e y=x3
63

68. 7.4. EXCEDENTE DO CONSUMIDOR
O excedente do consumidor representa a quantia total que os consumidores economizam quando adquirem
um certo produto, isto é, a diferença entre a quantia que os consumidores se dispõem a pagar pelo produto e o
valor real do produto.
q0
EC = (f(q)
p 0 )dq , onde p = f(q) representa o preço como função da demanda para um certo produto.
0
p
p0
p = f(q)
0
q0
q
O excedente do consumidor é dado pela área assinalada no gráfico acima e, representa o número de unidades
monetárias que os consumidores deixam de gastar quando o preço unitário de mercado é igual ao preço de
equilíbrio p0.
Exemplo:
A demanda de um produto é dada por p = 90 – 4q. Calcular o excedente do consumidor quando o preço de
mercado é R$ 10,00.
Solução:
Inicialmente, devemos encontrar a quantidade correspondente ao preço de mercado.
10 = 90 – 4q
20
20
(90 4q 10)dq
Logo, EC =
0
(80 4q)dq
4q = 80
80q 2q 2
0
Portanto, o excedente do consumidor é R$ 800,00.
64
q = 20
20
0
(1600 800) (0 0) 800

69. 7.5. EXCEDENTE DO PRODUTOR
O excedente do produtor representa a quantia total que os produtores lucram quando vendem um certo
produto, isto é, a diferença entre o valor real do produto e o valor que os produtores se dispõem a vender o
produto.
q0
EP = (p 0 - f(q))dq , onde p = f(q) representa o preço como função da oferta para um certo produto.
0
p
p = f(q)
p0
0
q0
q
O excedente do produtor é dado pela área assinalada no gráfico acima e, representa o número de unidades
monetárias que os produtores economizam quando o preço unitário de mercado é o preço de equilíbrio p0.
Exemplo:
A oferta de um produto é dada por p = 2q + 80. Calcular o excedente do produtor quando o preço de mercado é
R$ 100,00.
Solução:
Inicialmente, devemos encontrar a quantidade correspondente ao preço de mercado.
100 = 2q + 80
10
10
(100 (2q 80)dq
Logo, EP =
0
(20 2q )dq
2q = 20
20q q 2
0
q = 10
10
0
(200 100) (0 0) 100
Portanto, o excedente do Produtor é R$ 100,00.
E6) Considere as equações de oferta e demanda de um certo produto e o ponto de equilíbrio de mercado e
determine os excedentes do consumidor e do produtor:
1) p =
2q
+ 2 , p = –2q + 14
5
2) p = q2+ 2q , p = –q + 4
3) p = 2q + 3 , p = –q2 – 4q + 30
E7) Suponha que a equação da demanda de um determinado produto seja p =
excedente do consumidor se o preço for R$ 12,00.
65
300
(2q 1) 2
. Determine o

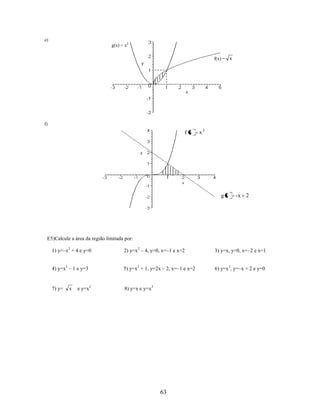
70. 7.6. SITES RELACIONADOS
http://www.geocities.com/puc3ware/tutoria_de_matamatica.html#integral_indefinida
http://www.somatematica.com.br/superior/integrais/integrais2.php
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm
http://pt.wikipedia.org/wiki/C%C3%A1lculo#Integrais
http://br.answers.yahoo.com/question/index?qid=20080223183956AAHLVc2
http://www.ufpi.br/uapi/conteudo/disciplinas/matematica/uni07_int_def_01.html
http://pessoal.sercomtel.com.br/matematica/superior/calculo/integral/integral.htm#int13
http://wwwp.fc.unesp.br/~arbalbo/arquivos/integraldefinida.pdf
http://pt.wikipedia.org/wiki/Integral
http://www.pucrs.br/famat/marcia/arquitetura/Integral_definida.pdf
http://www.dmat.ufba.br/mat042/aula10/aula10.htm
7.7. RESPOSTAS
E1) 1) 9
E2) 1)
9)
2)
9
20
2)
7
54
7
2
1
5
3)
40
3
10) 2 2 2
4)
11)
4
3
16
3
3
f ( x )dx
3
E4) a) 8 u.a.
32
3
8) 15
[f ( x ) g ( x )]dx
3)
1
0
32
5
7)
3
f ( x )dx
2)
4
E5) 1)
6)
6
f ( x )dx
4)
1
ln 2
2
34
3
2
E3) 1)
5)
2
4
g ( x )dx
[g ( x ) f ( x )]dx
5)
0
2
b)
2) 9
E6) 1) Ec = 25 , Ep = 5
32
u.a.
3
c)
32
u.a.
3
5
2
4)
2) Ec =
1
5
, Ep =
3
2
3)
d)5 u.a.
32
3
5) 9
e)
6)
3) Ec = 36 , Ep = 9
E7) Ec = 96
66
3
4
1
u.a.
3
7)
1
3
f)
3
u.a.
4
8)
1
2

71. 8. BIBLIOGRAFIA
CHIANG, Alpha C., WAINWRIGHT, Kevin. Matemática para economistas. 4.ed. Rio de janeiro:
Campus, 2006.
DOWLING, Edward T. Matemática aplicada à economia e administração. São Paulo : McGraw-Hill,
1981.
GOLDSTEIN, Larry J., LAY, David C.,SCHNEIDER, David I. Matemática aplicada:economia,
administração e Contabilidade. Porto Alegre : Bookman.2006.
LEITHOLD, Louis. Matemática aplicada à economia e administração. Tradução por
Carvalho Patarra. Universidade de São Paulo : Harbra, 1984.
Cyro de
MORETTIN, Pedro A., BUSSAB, Wilton O., HAZZAN, Samuel. Cálculo: funções de uma variável. São
Paulo : Atual, 1999.
___________. Cálculo: funções de várias variáveis. 2. ed.São Paulo : Atual, 1995.
MUROLO, Afrânio, BONETTO, Giácomo. Matemática aplicada à administração, economia e
contabilidade. São Paulo : Thomson Pioneira, 2004.
VERAS, Lilia Ladeira. Matemática aplicada à economia. 3.ed. São Paulo : Atlas, 1999.
SIMON, Carl P. Matemática para economistas. Porto Alegre : Bookmann, 2006.
TAN, Soo Tang. Matemática aplicada:à administração e economia. São Paulo: Pioneira 2005.
WEBER, Jean E. Matemática para economia e administração. 2.ed. São Paulo : Harper Row do
Brasil, 2001.
67

72. 9. APÊNDICE
1.CONJUNTO DOS NÚMEROS REAIS
Q I
a
/a, b
b
Onde: Q
Z, com b 0 é o Conjunto dos números racionais e I é o conjunto dos números
irracionais.
Exemplos:
0=
0
1
Q,
– 4=
4
1
3
=0,75(decimal finita)
4
Q,
5
1
25
Q,
Q,
2
=0,222...(decimal infinita e periódica)
9
Q,
2 1,414213... (decimal infinita e não periódica)
I,
π 3,141592... (decimal infinita e não periódica)
I,
2 3
3,464101... (decimal infinita e não periódica)
I,
6
3
0,816496... (decimal infinita e não periódica)
I,
0, – 4,
25 ,
3 2
6
, , 2 ,π,2 3 ,
4 9
3
Observações:
0
5
4
16
0,
2,
0
é indeterminado,
0
5
8
não existe ,
0
3 1,245730... ,
1
i
16
,
4
4,
3
2i
1.1. REPRESENTAÇÃO GEOMÉTRICA DO CONJUNTO
-2
-1
0 0,5 1
1
4
2
6
5
3
π
68
8
2,

73. 2. OPERAÇÕES COM FRAÇÕES
2.1. Adição e subtração de frações
Para adicionar(subtrair) frações, devemos reduzir as frações ao mesmo denominador e adicionar(subtrair) os
numeradores conservando o denominador comum.
Exemplo:
2
3
5
2
4
4 15 24
6
5
6
2.2. Multiplicação de frações
Para multiplicar frações, devemos multiplicar numerador com numerador e denominador com denominador.
Exemplo:
2 5
4. .
3 2
4.2.5
1.3.2
40
6
20
3
2.3. Divisão de frações
Para dividir frações, devemos multiplicar a primeira fração pelo inverso da segunda fração.
Exemplo:
2 5
:
3 2
2 2
.
3 5
4
15
3. SIMPLIFICAÇÃO DE FRAÇÕES
Para simplificar uma fração, devemos dividir o numerador e o denominador pelo máximo divisor comum de
ambos(maior número inteiro que divide os dois).
Exemplo:
36
. O máximo divisor comum entre 36 e 27 é 9. Portanto, devemos dividir o 36 e o 27 por 9,
27
36 : 9 4
27 : 9 3
Seja a fração
isto é:
36
27
69

74. 4. INTERVALOS
Sejam a,b
, com a < b.
4.1. Intervalo fechado de extremos a e b: [a,b] = x
a
/a
x
b
b
4.2. Intervalo aberto de extremos a e b: (a,b) = x
a
/a
x
b
b
4.3. Intervalo fechado à direita de extremos a e b: (a,b] = x
a
/a
a
/a
b
4.5. Intervalo infinito fechado à esquerda: [a,
)= x
/x
a
a
)= x
/x
a
a
4.7. Intervalo infinito fechado à direita: (
,a] = x
/x
a
a
4.8. Intervalo infinito aberto à direita: (
,a) = x
/x
a
Observação:
(
,
b
b
4.4. Intervalo fechado à esquerda de extremos a e b: [a,b) = x
4.6. Intervalo infinito aberto à esquerda: (a,
x
)=
70
a
x
b

75. Exemplo:
Determine se verdadeira ou falsa cada uma das afirmações abaixo:
a) [1,4] = (1,4)
b) [1,3]={1,2,3}
c) (2,4)={3}
d) (3,4)={ }
Solução
a) Falsa, o primeiro intervalo inclui o 1 e o 4, o segundo intervalo não.
b) Falsa, o primeiro intervalo inclui o 1, o 3 e todos os reais entre 1 e 3, o segundo é um conjunto
finito, constituído por três elementos o 1, o 2 e o 3.
c) Falsa, o primeiro intervalo inclui todos os reais entre 2 e 4, o segundo é um conjunto finito,
constituído por um único elemento o 3.
d) Falsa, o primeiro intervalo inclui todos os reais entre 3 e 4, o segundo é um conjunto vazio.
5. OPERAÇÕES COM CONJUNTOS
5.1. União ou Reunião
A operação união ou reunião de dois conjuntos A e B é o conjunto representado por A
B, formado
pelos elementos que pertencem a A ou a B.
Exemplos:
a) {-1,0,1,2}
b) (-1,2]
{1,2,3,4} = {-1,0,1,2,3,4}
[1,4) = (-1,4)
5.2. Intersecção
A operação intersecção de dois conjuntos A e B é o conjunto representado por A
elementos que pertencem simultaneamente aos conjuntos A e B.
Exemplos:
a) {-1,0,1,2}
b) (-1,2]
{1,2,3,4} = {1,2}
[1,4) = [1,2]
71
B, formado pelos

76. 5.3. Diferença
A operação diferença de dois conjuntos A e B, nessa ordem, é o conjunto representado por A – B, formado
pelos elementos que pertencem a A e não pertencem a B.
Exemplos:
a) {-1,0,1,2}–{1,2,3,4} = {-1,0}
b) (-1,2] – [1,4) = (-1,1)
E1) Represente graficamente os conjuntos:
1) (0, 3]
[1,5]
5) (–3, 4]
(0,
9)
(1,
2) [1, 4]
3) (–2, 3) – [0, 5)
6) [–2, 3) – [–3, 5)
)
)
10)
4) (
7)
[0,6)
8)
[2,
)
,2]
(1,7]
– {0,1,2}
– {–2}
6. PRODUTOS NOTÁVEIS
6.1. Quadrado da Soma: (a + b)2 = a2 + 2ab + b2
6.2. Quadrado da Diferença: (a – b)2 = a2 – 2ab + b2
6.2. Produto da Soma pela Diferença: (a + b).(a – b) = a2 – b2
Exemplos:
Desenvolva os produtos:
a) (3x + 2)2
b)(4x – 5)2
c) (2x + 3).(2x – 3)
Solução
a) (3x + 2)2 = (3x)2 + 2.(3x.2) + 22 = 9x2 + 12x + 4
b) (4x – 5)2 = (4x)2 – 2.(4x.5) + 52 = 16x2 – 40x + 25
c) (2x + 3).(2x – 3) = (2x)2 – 32 = 4x2 – 9
E2)Desenvolva os produtos:
1) (x + 3)2
2) (x – 2)2
6) (x – 1).(x + 1)
7) (2x +
1 2
)
2
3) (x + 5).(x – 5)
8) (x +
1
1
).(x – )
2
2
72
4) (1 – x)2
9) (
3
2x
+ )2
3
4
5) (2x – 3)2
10) (3x +
4
4
).(3x – )
5
5

77. 7. FATORAÇÕES COMUM E DIFERENÇA DE DOIS QUADRADOS
Fatorar uma expressão é escrever a expressão na forma de multiplicação.
Exemplos:
Fatore as expressões abaixo:
a) 18x4 + 12x2
b) 4x2 – 25
Solução:
a) Em 18x4 + 12x2 vamos aplicar a fatoração comum.
– O máximo divisor comum dos coeficientes 18 e 12 é 6.
– O máximo divisor comum da parte literal x4 e x2 é x2(letra comum com o menor expoente).
Portanto, vamos colocar em evidência o máximo divisor dos termos da expressão que é 6x 2.
18x4 + 12x2 = 6x2(
18x 4
12x 2
6x 2
6x 2
) = 6x2(3x2 + 2)
b) 4x2 – 25 é uma diferença de dois quadrados.
A forma fatorada de uma diferença de dois quadrados a 2 – b2 é (a + b)(a – b), então:
4x2 – 25 = (2x + 5)(2x – 5)
E3) Fatore as expressões:
1) 4x + 2x2
2) 3x2 – 6x
3) x3 + 5x2
4) x2 – 1
6) x4 – 4x2
7) x5 – x3
8) x5 + x4
9)
5) 4x2 – 9
x2 4
–
4 9
10) 9x3 –
8. RESOLUÇÃO DE EQUAÇÕES DE 1O GRAU
ax = b, com a
Solução :
Como a
0
0 , podemos dividir os dois membros por a,
Conjunto Solução:
S= x
/x
b
, com a
a
73
0
ax
a
b
b
daí, x = .
a
a
x
16

78. Exemplo:
Resolva a equação
Solução:
2x
3
2x
3
4
2x
2
–2x = 12
4
12
2
x = –6 ,
S ={-6}
E4) Resolva as equações:
1) –4x = 2
2)
x
4
3
5
3) –0,3x =
4) 2x + 4 = 1 – x
6) x + 3 =
8) (x – 2)2 = x2 + 3x
9)
1
3
x 2
2
7) 3x – 2 + x2 = x2 – 4
2x 4
5
5) 0,25x + 2 = 0,2x – 4
x
2
2
3
10) x2 – 9 = (x + 2)2
9. RESOLUÇÃO DE EQUAÇÕES DE 2O GRAU
ax2 + bx + c = 0, com a
Solução :
b
x=
b2
2a
0
4ac
Exemplo:
Resolva a equação –x2 +5x + 6 = 0
Solução: a = –1 , b = 5 e c = 6, logo: x =
Portanto x1 =
5 7
2
12
2
6 ou x2 =
5
52
4.( 1).6
2.( 1)
5 7
2
2
2
=
5
25 24
5 7
=
2
2
1 , S ={– 1,6}
E5) Resolva as equações:
1) x2 – 4 = 0
2) x2 – 4x = 0
3) x2 + 4 = 0
4) 2x2 + 3x = 0
5) x2 – 5x + 4 = 0
6) x2 + 4x + 4 = 0
7) x2 – 2x + 4 = 0
8) (x – 2)2 = x
9) 5x – 2 – 2x2 = 0
10) x2 – 9 = 1 – (x + 2)2
74

79. 10. PRODUTO NULO
a.b = 0
a = 0 ou b = 0
Exemplos:
Resolva as equações:
a) x2 – 4x = 0
b) x 5 – 9x3 = 0
Solução:
a) x2 – 4x = 0
x.(x – 4) = 0
b) x5 – 9x3 = 0
x = 0 ou x – 4 = 0
x3.(x2 – 9) = 0
x = 0 ou x = 4
x3 = 0 ou x2 – 9 = 0
x = 0 ou x =
3
E6) Resolva as equações:
1) (x – 4).(x +3) = 0
2) x.( x – 1).(x +2).(x2 – 9) = 0
5) x4 + 3x3 = 0
6) 2x5 + 6x4 = 0
9) x5 – 9x3 = 0
3) x2 – x = 0
10) x6 – 25x4 = 0
7) x3 – 5x2 + 4x = 0
4) x3 – 16x = 0
8) x4 + 4x3 + 4x2 = 0
11. RESOLUÇÃO DE INEQUAÇÕES DO 1O GRAU
Exemplo:
2x
3
Resolver a inequação
4
4
2 2
6
2
2
2x
3
2x
Solução:
2x
3
2
2x
3
2
4 2
x
3
2x
.3
3
2
x
2 .3
3 , S = [–3,
4) –0,3x
6
)
3
5
2x
–3
E7) Resolva as inequações:
1) 5x > 3
2) – 4x
5) 2x + 4 < 1 – x
6) 0,25x + 2
9) (x – 2)2
x2 + 3x
10)
x
2
1
3
2
3)
0,2x – 4
x
4
7) x + 3 >
2x 4
5
75
x 2
2
2
3
8) 3x – 2 + x2 < x2 – 4

80. 12. RESOLUÇÃO DE SISTEMAS DE EQUAÇÕES DO 1O GRAU
Exemplo:
2 x 3y
Resolver o sistema
x y
3
4
Resolução pelo método da substituição:
Isolando x na 2a equação temos: x = y + 4.
Substituindo o x obtido na 1a equação temos: 2( y + 4 ) + 3y = 3.
Resolvendo a equação do 1o grau obtemos: y = –1
Substituindo y = –1 na equação x = y + 4, obtemos x = 3.
Solução:
x
y
3
1
Resolução pelo método da adição:
2 x 3y
x y
3
4
Multiplicando-se a 2a equação por 3 obtemos:
2 x 3y
3
3x 3y 12
Adicionando membro a membro as duas equações temos: 5x = 15
x=3
Substituindo x = 3 na 2a equação do sistema dado obtemos: y = –1
Solução:
x
3
y
1
E8) Resolva os sistemas:
1)
6)
x
y
3
2)
x y 1
3x 7 y
0
5x 2 y
0
7)
x 2y
6
x 3y 1
x y
x 2y
6
2
3)
8)
3x y
6
x 2y
2
3x 5y 1
6x y
2
76
4)
9)
x 3y
0
4x y
22
x
2
x
4
y
3
y
2
1
10)
4
y
2
x
5)
x
2
y
3
4
2 x 3y
2
6
0,1x 0,25y 1

81. 13. POTÊNCIAS
Sejam a,b
e m,n {1,2,3,...}.
an
a. . a
aa 
 .
n vezes
Exemplos:
a) 25 = 2.2.2.2.2 = 32
b) (-3)5 = (-3). (-3). (-3). (-3). (-3) = -243
Propriedades
a) a0 = 1,
a 0
Exemplos:
a) 20 = 1
b) (-3)0 = 1
b) am.an = am+n
Exemplos:
a) 23 .22 = 25 = 32
b) (-3)2.(-3)3 = (-3)5 = -243
d) (a.b)n = an.bn
Exemplos:
a) (2.3)3 =23 .33 = 63 = 216
e)
am
am
an
n
b) (-3)2.(-3)2 = [(-3).(-3)]2 = 81
, a 0
Exemplos:
a)
f)
26
22
24
a
n
an
( 3) 5
( 3) 3
( 3) 2
27
, b 0
bn
b
b)
4
Exemplos:
a)
g) a m
3
2
3
n
23
3
3
( 3) 3
8
27
b)
64
b) ( 3) 3
( 2)
3
2
3
3
3
2
= am.n
Exemplos:
a) 2 2
3
2
6
77
2
( 3) 6
729
3
27
8

82. h) a-n =
1
an
,a 0
Exemplos:
a) 5
3
1
5
i)
n
1
125
3
a m = am/n , quando
b)
n
2
3
2
2
3
2
4
9
a
Exemplos:
a)
3
36
36 / 3
32
4
2
b)
9
2
4/2
2
2
1
4
E9) Calcule o valor de:
2
5
1) 34
2) (0,3)0
3)
7) (81)1/2
8) (16)1/4
1
4) 5-2
9) (-8)-1/3
5) (23 )2
6) (-0,1) -3
10) 25.2-9
11) (16)3/2
12) 2-4:2-10
E10)Aplique as propriedades adequadas:
3
1) x
2) x .x
1
3)
x
6) x 1/3
7) x 3/4
8) x-4:x-10
-5
10
5
4)
9)
x 25
x 20
3
x2
5) (x13 )5
10)
x
2
14. EQUAÇÃO PONTO-DECLIVIDADE
r: y – y1 = a(x – x1)
onde: P(x1, y1) é um ponto da reta r e a é a declividade da reta r.
Exemplo:
Escreva a equação da reta que passa pelo ponto P(–2 3) e tem declividade – 5.
Solução: x1 = –2 , y1 = 3 e a = –5
y – 3 = –5(x – (–2))
y – 3 = – 5x – 10
E11) Escreva a equação da reta que contém o ponto P e tem declividade a, sendo:
1)P( 2,3) e a = 5
2) P( -1,-3) e a = -2
4)P(
5) P( 2 ,0) e a =
2 , 2 ) e a = -3
3) P( 1/2,-6) e a = 2
6) P(-2,-3) e a = 1/2
2
78
y = – 5x – 7

83. 15. IMAGEM DE UMA FUNÇÃO NUM PONTO
Se para cada valor de x, a equação y = f(x) fornece um único valor para y, dizemos que esta equação define
uma função da variável x, onde:
– o domínio da função f é o conjunto de números reais, para os quais a função tem sentido.
– a imagem de x1 pela f é f(x1).
Exemplo:
Seja a função dada por f(x) =
x2 1
. Determine:
x 2
a) o domínio da f;
b) f(-1)
c) f(0)
d) f(1/2)
e) f(-2)
Solução:
a) Como o valor da função num ponto é o resultado de uma divisão, a função só tem sentido quando x + 2
O domínio da função é o conjunto dos números reais diferentes de –2, isto é, Dom f = (
( 1) 2 1
1 2
b) f(-1) é o valor da função f quando x = -1, logo f(-1) =
c) f(0) é o valor da função f quando x = 0, logo f(0) =
(0) 2 1
0 2
d) f(1/2) é o valor da função f quando x = 1/2, logo f(1/2) =
e) f(-2) é o valor da função f quando x = -2, como -2
1 1
1
1
2
2
1
2
(1 / 2) 2 1
1/ 2 2
1/ 4 1
5/ 2
5/ 2
5/ 2
Dom f, não existe f(-2)
E12) Achar os domínios das seguintes funções:
a)f(x) =
e)f(x) =
1
x 3
3 x
b) f(x) =
f) f(x) =
5
2x 1
x 3
x
x
i) f(x) =
2x 1
5x 10
2
c) f(x) = 6 3x
g) f(x) =
d) f(x) = 3 + x
2x
3 4x x
4
2
h) f(x) =
4
j) f(x) =
x
2
4
E13) Considere as funções do exercício anterior e determine f(-1) , f(0) e f(1).
79
, 2)
1
3
x 4
1
( 2,
0.
).

84. 16. RESPOSTAS
E1) 1)
0
5
2)
1
4
3)
-2
0
4)
7
5)
0
6)
4
{ }
7)
2
8)
0
1
2
9)
10)
-2
E2) 1) x2 + 6x + 9
2) x2 – 4x + 4
6) x2 – 1
7) 4x2 + 2x +
3) x2 – 25
1
4
8) x2 –
4) 1 – 2x + x2
1
4
9)
4x 2
9
2) 3x(x – 2)
3) x2(x + 5)
5) (2x – 3)(2x + 3)
6) x2(x – 2)(x + 2)
9)
1
2
2) S =
9
16
10) 9x 2
7) x3(x + 1)(x – 1)
8) x4(x + 1)
x
5) 4x2 – 12x + 9
E3) 1) 2x(2 + x)
E4) 1) S =
x
2
12
5
2
3
x
2
2
3
3) S =
10) x 3x
20
9
80
4) (x + 1)(x – 1)
1
4
3x
4) S = { -1}
1
4
5) S = { -120}
16
25

85. 6) S ={ -8}
E5) 1) S = {-2,2}
6) S = {0,-3}
E9)
2
,
1
)
2
3) S = (
,
)
8) S = (
x
0
y
0
x
4
3)
y 1
x
y
7)
10
4
8)
x
y
3)
7) 9
8) 2
9)
1
x5
2) x15
4
8) x6
E11) 1) y = 5x – 7
E12) A)
F)
2) y = –2x – 5
x
y
10) S = [
x
34
,
3
)
0
10)
x
y
15
2
1
6) –1000
11) 64
4) x5
, 1)
4
y
5)
5) 64
4)
3) y = 2x – 7
)
11
2
21
4
9)
5) S = (
)
2
x
10)
20
,
9
6
y
4)
1
25
1
10)
16
9) x 2 / 3
x3
5) S = {-3,0}
10) S = {-5,0,5}
4
9) S = [ ,
7
2
)
3
1
3
0
x
3) x3
7)
4) S = [
0
2
3
1
2
2) 1
12
)
5
2
y
1) 81
E10) 1)
4) S ={-4,0,4}
,
2)
10) S = {-3,1}
9) S = {-3,0,3}
7) S = ( 8,
)
5) S = {1,4}
1
2
9) S = 2,
3) {0,1}
13
4
10) S =
3
2
4) S = 0,
8) S = {0,-2}
2) S = (
y 1
6)
8) S = {1,4}
7) {0,1,4}
)
6) S = [120,
x
3) { }
2) S = {-3,-2,0,1,3}
34
3
9) S =
7) { }
E6) 1) S = {-3,4}
E8)1)
4
7
8) S =
2) S = {0,4}
6) S = {-2}
3
E7) 1) S = ( ,
5
2
3
7) S =
12) 64
6) 3 x
5) x65
1
, para x 0
x
4) y = –3x + 4 2 5) y =
{3}
B)
{ 2}
C) (
,2]
D) [0,
{ 2,2}
G)
{1,3}
H)
{4}
I) [1/2,
E13) A)
1 1 1
,
,
4 3 2
B)
3
1 1
,
,
5 10 15
C) 3, 6 , 3
F)
2 3 4
,
,
3 4 3
G)
1
, 0 , NE
4
H)
1
3
81
5
,
E) (0,
)
)
4
,
1
3
3
I)
x
–2
2
)
J)
D) NE, 3 , 4
1
3
2 x – 2 6)y =
5
E) NE, NE , 2
3 , -1 , 1
J)
4 4
,1,
5 5

86. 17. DERIVADAS DE FUNÇÕES DE UMA VARIÁVEL
17.1. DERIVADA DE UMA FUNÇÃO OU FUNÇÃO DERIVADA
y
x
f ’(x) = lim
x
Notações:
f ’(x) , Dx f(x) ,
0
d
f (x)
dx
f (x
lim
x
x) f (x)
x
0
ou y’ , Dx y ,
dy
,se y = f(x).
dx
Exemplo: f(x) = 2x + 1
f' x
lim
Δx
0
2 x Δx
2x 1
0
1
Δx
2x 1
0
2x 2 x 1
Δx
lim
Δx
lim
Δx
0
2x 2 x 1 - 2x - 1
Δx
0
2 x
Δx
lim
Δx
lim
Δx
lim
Δx
f x Δx f x
Δx
2
0
2
17.2. REGRAS DE DERIVAÇÃO
1. DERIVADA DA FUNÇÃO CONSTANTE
Dx c = 0
Exemplos:
a) Dx 5 = 0
b) Se f(x) =
3
então f’(x) = 0
2
2. DERIVADA DA FUNÇÃO IDENTIDADE
Dx x = 1
3. DERIVADA DA FUNÇÃO EXPONENCIAL NATURAL
(ex)’= ex
82
c) Se y = e então y’ = 0

87. 4. DERIVADA DA FUNÇÃO LOGARITMO NATURAL
(ln x )’=
1
x
5. DERIVADA DA SOMA DE DUAS FUNÇÕES
(f(x)+ g(x))’= f ’(x)+ g ’(x)
Exemplos:
a) Dx ( 5 + ex ) = 0 + ex = ex
b) Se f(x) = x – ln x então f’(x) = 1 –
1
x
6. DERIVADA DO PRODUTO DE UMA CONSTANTE POR UMA FUNÇÃO
(c.f(x))’ = c.f ’(x)
Exemplos:
a) Dx 5x = 5.1 = 5
b) Se f(x) =
3 ln x
3 1
então f’(x) = .
2
2 x
3
2x
E1) Encontre y’, sabendo que:
1) y = x – 3
2) y = ex + 5
3) y = 4 – ln x
4) y = 2x + e
5) y = 7 – 6x
6) y = 3e x + 8ln x –1
7) y =
12 x 9
3
8) y =
12 x 9
5
9) y =
x
3
ln x
2
5
10) y = ln 4 – 3e + 2 -1
7. DERIVADA DA FUNÇÃO POTÊNCIA
(xp)’= pxp-1
Exemplos:
a) Dx x3 = 3x2
c) Se y =
1
x
4
b) Se f(x) =
, y = x-4 então y’ = – 4x-5 =
3 x
3
x 3 , f(x) = x3/2 então f’(x) = .x 1 / 2 =
2
2
4
x5
83

88. E2) Encontre y’, sabendo que:
2) y =
4) y =
2x 2
3x
x
x2 1
x 1
3) y = x 3
3x e
6) y =
2e x
3
2x
8) y = 3x3.(2 + 4x)
33 x
7) y = 2 x
x2
2
5) y =
1) y = x4 – 3x2 + 2x – 3
2
x e2
1
x
9) y = (x 2 – 1)(2 + x)
1
10) y =
x
8. DERIVADA DO PRODUTO DE DUAS FUNÇÕES
(f(x).g(x))’= f(x).g’(x) + g(x).f ’(x)
Exemplo:
Dx (x3.ln x ) = x3.
1
+ .ln x . 3x2 = x2 + 3x2.ln x = x2.(1 + 3ln x)
x
9. DERIVADA DO QUOCIENTE DE DUAS FUNÇÕES
f (x)
g( x )
'
g( x).f ' ( x ) f ( x).g' (x )
[g( x )] 2
Exemplo:
Se f(x) =
(1 4x ).2 (2x 3)( 4)
2x 3
então f’(x) =
1 4x
(1 4x ) 2
2 8x 8x 12
(1 4x )
2
10
(1 4x ) 2
E3) Encontre y’, sabendo que:
1) y = x.ln x
2) y = 3x 2ex
5) y = ex lnx
6) y =
9) y =
2
3 2x
10) y =
ex
2x
2 3x
1 x
4) y =
x2 2
1 2x
7) y = 5x3ln x
8) y =
3( x 2 1)
x
3) y =
x2 1
x 1
84

89. 10. DERIVADA DA COMPOSTA DA POTÊNCIA COM UMA FUNÇÃO f
([f(x)]p)’ = p.[f(x)]p-1.f ’(x)
Exemplos:
a) Dx (x3– 1)5 = 5.(x3– 1)4. 3x2 = 15x2.(x3– 1)4
b) Se f(x) = 2x 6 , f(x) = (2x + 6)1/2 então f’(x) =
1
c) Se y =
(1 x )
4
1
.(2x 6)
2
1/ 2
, y = (1 – x)-4 então y’ = – 4.(1 – x )-5.(-1) =
1
.2 =
2x 6
4
(1 x ) 5
E4) Encontre y’, sabendo que:
1) y = (2 – x)6
5) y =
2) y = 3(5x + 4)5
4
3(1 2x )3
3
6) y =
2( x
2
9) y =
2
4) y =
7) y = 4 x 2
4x ) 2
8) y =
1
(2x 3) 5
x2
5
3
10) y =
3
2 x2
1 x
3) y = (x2 + 3x – 1)2
2
11. DERIVADA DA COMPOSTA DA FUNÇÃO EXPONENCIAL NATURAL COM UMA FUNÇÃO f
(ef(x) )’= ef(x) .f ’(x)
Exemplos:
a) Dx e x
3
1
= ex
b) Se f(x) = e 2 x
1
c) Se y =
e
4x
6
3
1
. 3x2 = 3x2. e x
3
1
, então f’(x) =2. e 2 x
6
4
, y = e-4x então y’ = – 4.e-4x =
e
4x
E5) Encontre y’, sabendo que:
1) y
ex
4) y = e
2 5
x2
2) y =
5) y =
1
3) y = e 3x
ex
e
x2
2
85
6) y =
e 3x
1 x
2

90. 12. DERIVADA DA COMPOSTA DA FUNÇÃO LOGARITMO NATURAL COM UMA FUNÇÃO f
(ln f(x) )’ =
f ' (x)
f (x)
Exemplos:
3x 2
a) Dx ln(x3– 1) =
x3 1
1
(2 x 6) 1 / 2 .2
1
1/2
2
b) Se f(x) =ln(2x + 6) então f’(x) =
=
1/ 2
2x 6
( 2 x 6)
Importante: Como as funções y = ex e y = ln x são inversas, e ln u = u e ln eu = u
E6) Encontre y’, sabendo que:
1) y =3ln x2
2) y = ln (5x+2)
5) y = x2.ln x3
E7) Se f(x) =
2x 1
6) y = e
3) y = ln(4-5x)
ln 3 x
4) y = e 2x . ln 2x
7) y = ln e5x
, determine :
1 x
1) f ’(0)
2) f ’’(2)
3) f ’’’(0)
4) f (4)(2)
E8) Resolve as equações f’(x) = 0, para:
a)f(x) = x2 – 4
b) f(x) = x 2 – 3x + 2
c) f(x) = 5x – 4
d) f(x)=x4– 8x2 – 5
e) f(x)= x4– 4x3
f) f(x)= x3– 12x+4
g) f(x)=x3– 3x2+5
h) f(x)= 3x5– 5x3
i) f(x) =
x3
3
2x 2
3x 10
j) f(x) =
x3
3
3 2
x
2
86
2x 1

91. 17.3. INTERPRETAÇÃO GEOMÉTRICA DA DERIVADA DE UMA FUNÇÃO NUM
PONTO
A derivada f ’(x1), se existir, fornece a declividade da reta tangente ao gráfico de uma função f no ponto
P(x1 , f(x1)).
y
f
f(x1)
t
P
0
x1
x
f ’(x1) = at
Importante: Da Geometria Analítica, a equação de uma reta, não vertical, que passa pelo ponto P(x 1,y1) e tem
declividade a é
y – y1 = a(x – x1)
Exemplo:
Determine a equação da reta tangente ao gráfico da função logaritmo natural no ponto de abscissa 1.
Solução:
f(x) = ln x
Se o ponto de tangência P tem abscissa x1 = 1, a ordenada y1 é f(x1) = f(1) = 0.
A declividade da reta tangente ao gráfico da f no ponto P é a = f’(x 1) = f’(1) = 1.
Portanto, a equação da reta tangente é y – 0 = 1(x – 1) ou y = x – 1.
E9) Seja a função definida por f(x) = x2.
1)Calcule a declividade da reta tangente ao gráfico de f no ponto x = 1.
2)Encontre a equação da reta tangente ao gráfico de f no ponto x = 1.
3)Esboce os gráficos de f e da reta tangente, no mesmo sistema de eixos.
E10) Seja a função definida por f(x) = 4x – x2 no ponto P(1, 3).
1)Encontre a derivada da função f.
2)Calcule a declividade da reta tangente ao gráfico de f no ponto P.
3) Escreva a equação da reta tangente, no ponto P.
87

92. 17.4. APLICAÇÕES DE DERIVADAS
1. CUSTO MARGINAL : Cmg(x) = C’(x)
Sendo C a função Custo Total para produzir “x ” unidades de um certo produto, chama-se Custo Marginal
a derivada da função Custo Total em relação a x.
E11) Se a função Custo Total é dada por C(x) = x3 – 30x2 + 400x + 500, determine a função custo marginal.
Observação: Da definição de derivada: C’(x) = lim
x
Para
x muito pequeno C’(x)
C( x
No exemplo acima: Cmg(10) = 100
C( x
0
x ) C( x )
x
x ) C( x )
, fazendo
x
x = 1, tem-se: Cmg
C( x 1) C( x )
1
C(11) – C(10) = 101.
Então, o custo marginal é aproximadamente a variação do custo decorrente da produção de uma unidade
adicional. No exemplo, Cmg(10) é aproximadamente o custo da décima primeira unidade.
2. RECEITA MARGINAL : Rmg(x) = R’(x)
Se R é a função Receita Total decorrente da venda de “x ” unidades de um certo produto, chamamos de
Receita Marginal a derivada da função Receita Total em relação a x.
E12) Se a função Receita Total é dada por R(x) = – 2x2 + 100x, determine a função receita marginal.
Observação: Do mesmo modo que a custo marginal, a receita marginal representa, aproximadamente, a
variação da receita total devido a venda de uma unidade a mais, a partir de “x ” unidades.
No exemplo anterior: Rmg(5) = 80
R(6) – R(5) = 78. Então, a receita marginal calculada
no ponto 5 é a variação aproximada da receita decorrente da venda da 6 a unidade.
3. LUCRO MARGINAL : Lmg(x) = L’(x)
Se L é a função Lucro Total decorrente da produção e venda de “x ” unidades de um certo produto,
chamamos de Lucro Marginal a derivada da função Lucro Total em relação a x.
88

93. E13) Se a função Receita é dada por R(x) = –2x2 + 100x e a função Custo Total dada por
C(x) = x2 +10x + 375, onde x representa a quantidade produzida e vendida, determine:
1) a função Lucro Total;
2) a função Lucro Marginal;
3) o lucro marginal ao nível de 10 unidades;
4) a interpretação do resultado 3.
E14) Se a função Receita Total é dada por R(x) = 100x e a função Custo Total C(x) = x 2 +20x + 700, onde x
representa a quantidade produzida e vendida, determine:
1) a função Custo Marginal;
2) a função Receita Marginal;
3) a função Lucro Total;
4) a função Lucro Marginal;
5) o custo de produção de 11 unidades;
6) o custo de produção da 11a unidade;
7) use a função Custo Marginal para estimar o custo de produção da 11 a unidade;
8) a receita decorrente da venda de 11 unidades;
9) a variação da receita decorrente da venda da 11a unidade;
10) use a função Receita Marginal para estimar a variação da receita decorrente da venda da 11 a unidade;
11) o lucro decorrente da produção e venda de 11 unidades;
12) a variação do lucro decorrente da produção e venda da 11a unidade;
13) use a função Lucro Marginal para estimar a variação do lucro decorrente da produção e venda da 11 a
unidade;
E15) Dadas as funções Receita e Custo R(x) = – x2 + 9x e C(x) = 2x + 6, determine o Lucro Marginal no
x = 2 e interprete o resultado obtido.
89

94. 17.5. SITES RELACIONADOS
http://pessoal.sercomtel.com.br/matematica/superior/calculo/derivada/derivada1.htm
http://www.qfojo.net/criar+/mat/deriv/derivadas.htm
http://pt.wikipedia.org/wiki/Derivada
http://www.vestibular1.com.br/revisao/tabela_derivadas.pdf
http://www.cepa.if.usp.br/e-calculo/
http://www.google.com.br/search?sourceid=navclient&ie=UTF8&rlz=1T4SUNA_enBR239BR240&q=fun%c3%a7%c3%b5es+marginais
http://www.neema.ufc.br/Ern_cap2_parte2.htm
17.6. RESPOSTAS
1
x
12
8) y’=
5
2) y’= e x
E1) 1) y’= 1
8
x
6) y’= 3ex +
7) y’= 4
E2) 1) y’= 4x3 – 6x + 2
5) y’ = 1
3) y’=
9) y’=
3
1
3
2
x
x
1
3
5) y’= –6
1
2x
10) y’= 0
3) y’= 3x2 –2ex –
2) y’= x – 3
6) y’= -
9) y’=3x2 + 4x – 1
4) y’= 2
7) y’=
1
x
1
3
x
4) y’= 2
8) y’ = 18x2 + 48x3
2
1
10) y’ =
2 x3
E3) 1) y’= 1 + ln x
2) y’=3x e x (2 + x)
3) y’=
1
(1 x )
5) y’= ex (
9) y’=
1
+ln x)
x
4
(3 2x ) 2
6) y’=
e x ( x 1)
2x
2
7) y’= 5x2(1+3ln x)
2
4) y’=
8) y’=
2x 2
(1 2 x ) 2
3x 2
x
10) y’= 1
90
2x 4
3
2

95. E4) 1) y’= – 6(2 – x)5
8
5) y’=
(1 2 x )
E5) 1) y’ = 2xe x
5) y’ = xe
2
(x
4x )
3
5
2) y’ =- e
x2
2
6) y’=
2) y’=
5) y’= 2xln x3+3x
E8) 1) x = 0
6) x = -2 , x = 2
(2x 3) 6
x
8) y’=
x
2
5
(x
2
2) 4
x
3) y’ = 3e 3x
2
4) y’ = 2xe
x2
e 3 x ( 4 3x )
(1 x ) 2
5
5x 2
3) y’=
5
4 5x
4) y’= e 2 x (
1
x
2 ln 2x )
7) y’= 5
4) –24
3) 6
2) x =
10
4x 2
6) y’= 3
2) –2
2
7) y’=
3
4) y’=
x
3
6
x
E7) 1) 1
2
10) y’=
(1 x )
3) y’=(4x + 6)( x2 + 3x – 1)
6x 12
6) y’=
4
1
9) y’=
E6) 1) y’=
2) y’ = 75(5x + 4)4
3
2
3) NE
7) x = 0 , x = 2
E9) 1) 2
8) x = 0 , x = -1 , x = 1
2) 2
5) x = 0 , x = 3
9) x = 1 , x = 3
10) x = 1 , x = 2
2) y = 2x – 1
E10) 1) f’(x) = 4 – 2x
4) x = 0 , x = -2 , x = 2
3) y = 2x + 1
E11) Cmg = 3x2 – 60x + 400
E12) Rmg = – 4x + 100
E13) 1) L = –3x2 + 90x – 375
2) Lmg = – 6x + 90
3) 30
E14) 1) Cmg = 2x + 20
2) Rmg = 100
3) L = –x2 + 80x – 700
5) 1041
10) 100
6) 41
7) 40
8) 1100
11) 59
12) 59
13) 60
E15) 3
91
4) Lmg = – 2x + 80
9) 100

96. 18. BIBLIOGRAFIA
MORETTIN, Pedro A., BUSSAB, Wilton O., HAZZAN, Samuel. Cálculo: funções de
Paulo : Atual, 1999.
SILVA, Sebastião Medeiros da. Matemática para os Cursos de economia,
contábeis. São Paulo : Atlas, 1981.
92
uma variável. São
administração e ciências