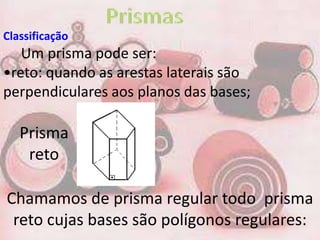
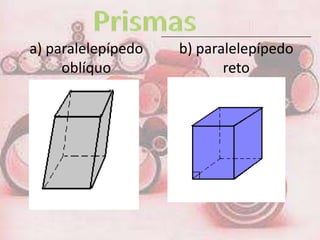
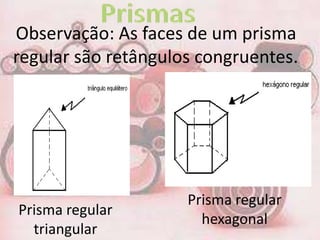
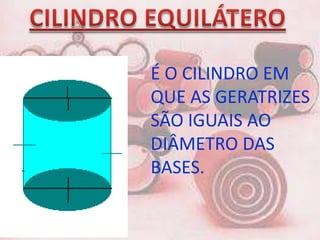
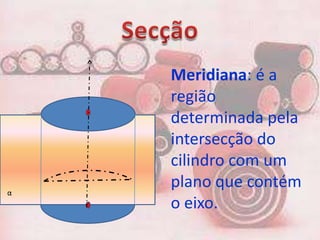
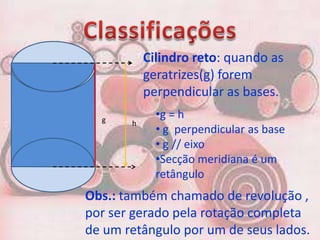
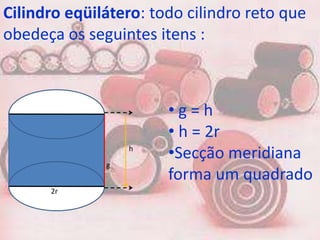
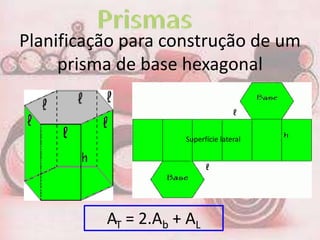
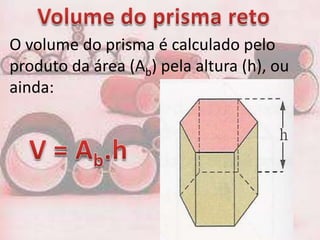
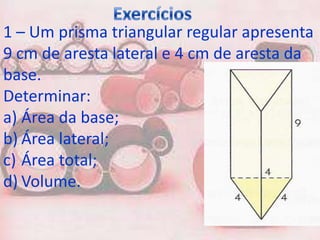
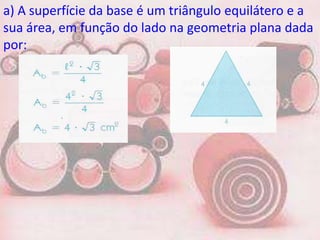
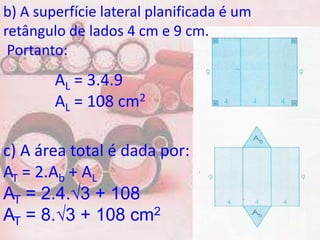
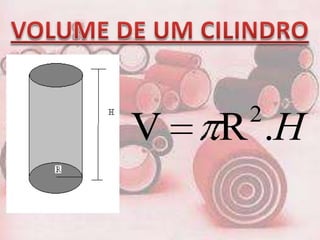
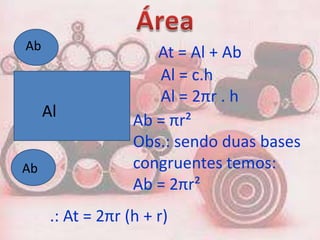
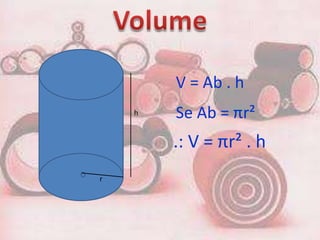
1. Um prisma pode ser reto ou oblíquo. Um prisma regular tem bases polígonos regulares e faces retangulares. 2. O documento fornece fórmulas para calcular a área da base, área lateral e área total de prisma, bem como o volume. Exemplos mostram cálculos para prisma triangular, quadrangular e hexagonal.

2. Classificação
Um prisma pode ser:
•reto: quando as arestas laterais são
perpendiculares aos planos das bases;
Prisma
reto
Chamamos de prisma regular todo prisma
reto cujas bases são polígonos regulares:

3. a) paralelepípedo b) paralelepípedo
oblíquo reto

4. Observação: As faces de um prisma
regular são retângulos congruentes.
Prisma regular
Prisma regular
hexagonal
triangular

5. Planificação para construção de um
prisma de base hexagonal
Superfície lateral
AT = 2.Ab + AL

6. O volume do prisma é calculado pelo
produto da área (Ab) pela altura (h), ou
ainda:

7. 1 – Um prisma triangular regular apresenta
9 cm de aresta lateral e 4 cm de aresta da
base.
Determinar:
a) Área da base;
b) Área lateral;
c) Área total;
d) Volume.

8. a) A superfície da base é um triângulo equilátero e a
sua área, em função do lado na geometria plana dada
por:

9. b) A superfície lateral planificada é um
retângulo de lados 4 cm e 9 cm.
Portanto:
AL = 3.4.9
AL = 108 cm2
c) A área total é dada por:
AT = 2.Ab + AL
AT = 2.4.√3 + 108
AT = 8.√3 + 108 cm2

10. d) O volume á dado por:
V = Ab.h
V = 4.√3.9
V = 36.√3 cm3
A altura é igual à aresta
lateral.

11. 2 – seja um prisma quadrangular de aresta
da base igual a 6 cm e aresta lateral igual a
12 cm. Determine:
a) Área da base
b) Área lateral
c) Área total
d) volume

12. 3 – Um prisma hexagonal regular tem
6√3m de aresta lateral e 2m de aresta
da base. Determinar:
a) Área da base;
b) Área lateral;
c) Área total;
d) Volume.

13. a) A superfície da base é um hexágono
regular de lado l.
A superfície lateral planificada é um retângulo
de lados 12 m e 6√3m.

14. 4 – Considere o prisma
hexagonal representado ao
lado. Indicar:
a) As faces visíveis;
b) Dois planos
concorrentes;
c) Dois planos paralelos que
não sejam da base.

15. 5 – Calcule a área da base, a área lateral, a
área total e o volume em cada caso:
a) Prisma quadrangular de aresta lateral 8
cm e aresta da base 4 cm.
b) Prisma triangular regular de aresta
lateral 2 cm e aresta da base 4 cm
c) Prisma hexagonal regular de aresta
lateral 6 cm e aresta da base 3 cm

17. É um tipo de corpo redondo. Possui duas faces planas
circulares (bases) e uma face não-plana
(arredondada).
O volume de um cilindro é determinado pelo produto
da área da base pela medida da altura.
V = Ab . h
V = r² . h

19. • Cilindro circular reto é um corpo redondo
formado pela ligação entre infinitos vértices
pertencentes a dois círculos iguais e paralelos.
Fórmulas:
• Área da base(AB): nr2
• Área lateral(AL): 2.n.r.h
• Área total(AT): 2.AB + AL

20. É o cilindro em
que o eixo é
perpendicular à
base.

21. É O CILINDRO EM
QUE AS GERATRIZES
SÃO IGUAIS AO
DIÂMETRO DAS
BASES.

22. 2
V R .H

23. AT 2 AB AL
2
AB 2 R
AL 2 R.H
AT 2 R( R H )

24. Meridiana: é a
região
determinada pela
intersecção do
cilindro com um
α
plano que contém
o eixo.

25. Cilindro reto: quando as
geratrizes(g) forem
perpendicular as bases.
g
•g = h
h
• g perpendicular as base
• g // eixo
•Secção meridiana é um
retângulo
Obs.: também chamado de revolução ,
por ser gerado pela rotação completa
de um retângulo por um de seus lados.

27. Cilindro eqüilátero: todo cilindro reto que
obedeça os seguintes itens :
•g=h
• h = 2r
h
•Secção meridiana
g
forma um quadrado
2r

28. r Se trata de um
comp.=2 π r
retângulo cujo
comprimento
Larg.=h tem tamanho
igual ao
comprimento da
circunferência, e
teremos dois
círculos
congruentes.

29. Ab
At = Al + Ab
Al = c.h
Al = 2πr . h
Al
Ab = πr²
Obs.: sendo duas bases
Ab congruentes temos:
Ab = 2πr²
.: At = 2πr (h + r)

30. V = Ab . h
h Se Ab = πr²
.: V = πr² . h
r

31. 1. Um tanque, na forma de um cilindro regular
com 10cm de altura e de diâmetro (medidas
externas), tampado superiormente, é usado
como deposito de óleo combustível.
Anualmente, é feita uma pintura de sua
superfície externa (excluindo-se a pintura da
base inferior).Sabe-se que, com uma lata de
tinta, pintam-se 26m² da superfície.
Considerando π=3,14, para se pintar todo o
tanque são necessários, aproximadamente:

32. h=10cm
a) 7 latas
b) 15 latas
c) 18 latas
d) 20 latas
d=10cm e) 21 latas

33. 2. Para medir o volume de uma pedra
irregular,um estudante utilizou um copo de
forma cilíndrica, de diâmetro 6cm, com água
até certa altura. Marcou o nível da água em
repouso, deixou a pedra mergulhar e marcou
o novo nível. Considerando π=3,14, se o
desnível observado foi de 2cm, então o
volume da pedra é:
R: 56,52 CM3

34. 3 – Calcule a área total e o volume de um
cilindro que tem raio da base r= 2 cm e
altura h= 5cm.
4 – Determine a área total de um cilindro
eqüilátero que possui volume igual a 128π
cm3.
4 – Se um cilindro eqüilátero tem volume
16π cm3, dê o valor de:
•A medida do raio da base;
•A altura;
•A área total.

35. 5 – Calcule o raio e a altura de um cilindro
reto, sabendo que o seu volume é 28π cm3
e sua área lateral é 28π cm2.
6 – Calcule a área total de um cilindro reto,
sabendo que seu volume é 144π cm3 e sua
secção meridiana tem área de 72 cm2.
7 – Calcular a área e o volume do cilindro
equilátero de altura 10 cm.

36. 8 – (UFMG) Achar a área total da superfície de
um cilindro reto, sabendo que o raio da base é
de 10cm e a altura é de 20cm.
Resp. → At = 1.884cm
9 – A altura de um cilindro reto vale 6cm e
o raio da base mede 2cm. Determine a área
total e o volume do cilindro.
.
10 – O volume de um cilindro equilátero
vale 54 cm3. Determine o raio da base e a
área total desse cilindro

38. Um cilindro equilátero tem volume V = 16 π cm³. Calcule a altura desse cilindro.
Em um cilinro circular reto a área lateral é
54 π cm² e a medida da altura é o triplo da
medida do raio da base. Calcule o volume
desse cilindro.
A área lateral de um cilindro equilátero é 16 π
cm². Calcule a área da base
Uma secção meridiana de um cilindro
equilátero tem 144 π cm² de área. Calcule a
área lateral, área total e o volume desse
cilindro.
Calcule o volume de um cilindro
equilátero cujo raio da base mede 4 cm

39. Um cilindro circular reto re raio da base 5 cm
possui uma secção meridiana equivalente a
uma de suas bases ( Asm = Ab ). Calcule a área
lateral, a área total e o volume desse cilindro.