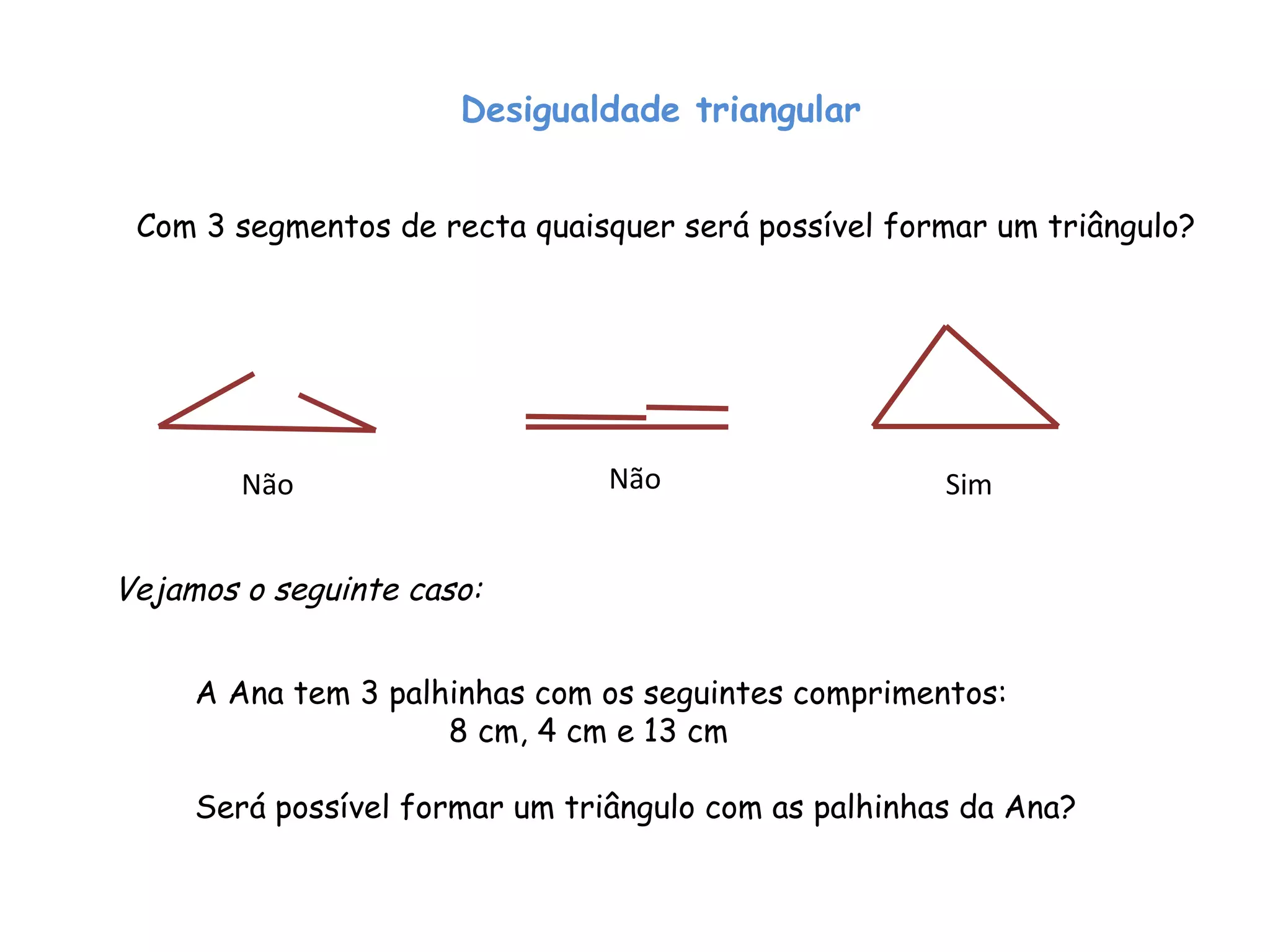
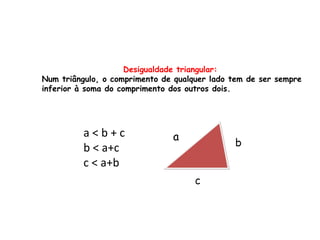
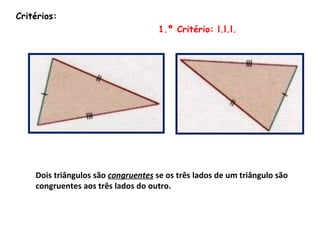
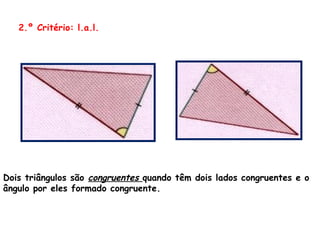
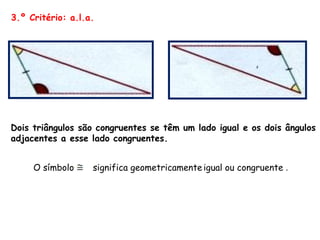
1) Não é possível formar um triângulo com 3 segmentos de comprimentos quaisquer. 2) Ana não pode formar um triângulo com suas 3 palhinhas de comprimentos 8cm, 4cm e 13cm. 3) Dois triângulos são congruentes se tiverem 3 lados ou 2 lados mais o ângulo entre eles ou 1 lado e os 2 ângulos adjacentes iguais.

1. Desigualdade triangular Com 3 segmentos de recta quaisquer será possível formar um triângulo? Não Não Sim Vejamos o seguinte caso: A Ana tem 3 palhinhas com os seguintes comprimentos: 8 cm, 4 cm e 13 cm Será possível formar um triângulo com as palhinhas da Ana?

2. Desigualdade triangular: Num triângulo, o comprimento de qualquer lado tem de ser sempre inferior à soma do comprimento dos outros dois. a < b + c b < a+c c < a+b a b c

3. Construção e Congruência de triângulos Dois triângulos dizem-se geometricamente iguais se se podem sobrepor ponto por ponto, isto é, se coincidem um com o outro, quando se sobrepõem. Assim, em dois triângulos geometricamente iguais, a cada lado de um triângulo vai corresponder no outro um lado de igual medida; e a cada ângulo de um triângulo vai corresponder no outro um ângulo geometricamente igual. De um para o outro, os elementos iguais dizem-se correspondentes ou homólogos. Será que para concluirmos que dois triângulos são iguais, teremos de comparar sempre, os 3 lados de um com os 3 lados do outro e comparar sempre os 3 ângulos de um com os 3 ângulos do outro?

4. Critérios: 1.º Critério: l.l.l. Dois triângulos são congruentes se os três lados de um triângulo são congruentes aos três lados do outro.

5. 2.º Critério: l.a.l. Dois triângulos são congruentes quando têm dois lados congruentes e o ângulo por eles formado congruente.

6. 3.º Critério: a.l.a. Dois triângulos são congruentes se têm um lado igual e os dois ângulos adjacentes a esse lado congruentes. O símbolo significa geometricamente igual ou congruente .