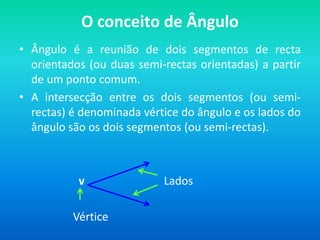
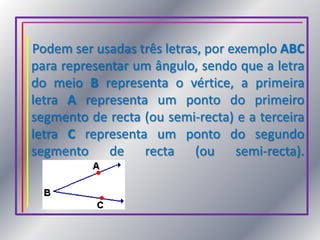
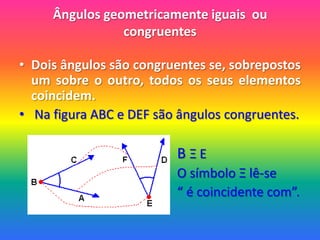
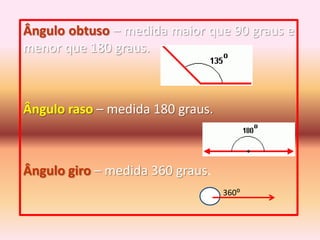
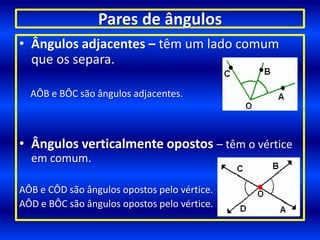
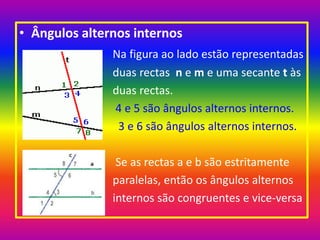
1) O documento discute o conceito de ângulo, definindo-o como a reunião de dois segmentos de reta orientados a partir de um ponto comum chamado vértice. 2) Explica como medir ângulos usando um transferidor, colocando o vértice no centro e alinhando um lado com a escala de 0 a 180 graus. 3) Discutem tipos de ângulos como agudos, retos e obtusos, bem como pares de ângulos como adjacentes e opostos.

1. MatemáticaTema: Ângulos

2. O conceito de ÂnguloÂngulo é a reunião de dois segmentos de recta orientados (ou duas semi-rectas orientadas) a partir de um ponto comum.A intersecção entre os dois segmentos (ou semi-rectas) é denominada vértice do ângulo e os lados do ângulo são os dois segmentos (ou semi-rectas). v Lados Vértice

3. Podem ser usadas três letras, por exemplo ABC para representar um ângulo, sendo que a letra do meio B representa o vértice, a primeira letra A representa um ponto do primeiro segmento de recta (ou semi-recta) e a terceira letra C representa um ponto do segundo segmento de recta (ou semi-recta).

4. Segmentos de recta e semi-rectaLembramos que um segmento de recta orientado AB é um segmento de recta que tem início em A e final em B. A BUma semi-recta orientada AB é a parte de uma recta que tem início em A, passa por B e se prolonga indefinidamente. A B

5. O TransferidorPara obter a medida aproximada de um ângulo traçado em um papel, utilizamos um instrumento denominado transferidor, que contém um segmento de recta em sua base e um semicírculo na parte superior marcado com unidades de 0 a 180. Alguns transferidores possuem a escala de 0 a 180 marcada em ambos os sentidos do arco para a medida do ângulo sem muito esforço.

6. Para medir um ângulo, coloque o centro do transferidor (ponto 0) no vértice do ângulo, alinhe o segmento de recta OA (ou OE) com um dos lados do ângulo e o outro lado do ângulo determinará a medida do ângulo, como mostra a figura.

7. Na figura acima, podemos ler directamente as medidas dos seguintes ângulos:

8. Ângulos geometricamente iguais ou congruentesDois ângulos são congruentes se, sobrepostos um sobre o outro, todos os seus elementos coincidem. Na figura ABC e DEF são ângulos congruentes.B Ξ E O símbolo Ξ lê-se “ é coincidente com”.

9. Com relação às suas medidas, os ângulos podem ser classificados como: recto, agudo, obtuso, raso e giro.Ângulo agudo – medida maior que 0 graus e menor que 90 graus. Ângulo recto – medida 90 graus.

10. Ângulo obtuso – medida maior que 90 graus e menor que 180 graus.Ângulo raso – medida 180 graus.Ângulo giro – medida 360 graus.360⁰

11. Pares de ângulosÂngulos adjacentes – têm um lado comum que os separa.AÔB e BÔC são ângulos adjacentes.Ângulos verticalmente opostos – têm o vértice em comum.AÔB e CÔD são ângulos opostos pelo vértice. AÔD e BÔC são ângulos opostos pelo vértice.

12. Ângulos complementares – são ângulos cuja soma das amplitudes é 90 graus.< a + < b = 90⁰ab• Ângulos suplementares – são ângulos cuja soma das amplitudes é 180 graus. c < c + < d = 180⁰ d

13. Ângulos alternos internos Na figura ao lado estão representadas duas rectas n e m e uma secante t às duas rectas. 4 e 5 são ângulos alternos internos. 3 e 6 são ângulos alternos internos. Se as rectas a e b são estritamente paralelas, então os ângulos alternos internos são congruentes e vice-versa