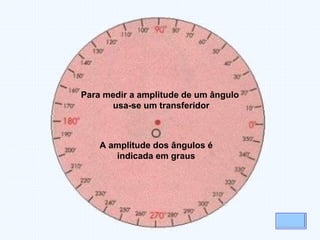
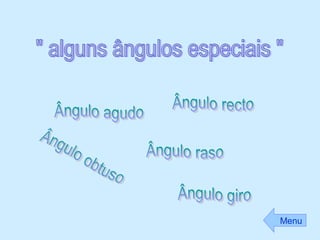
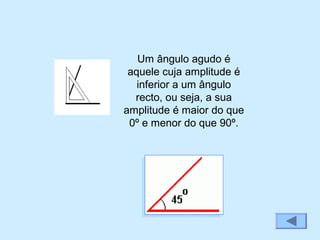
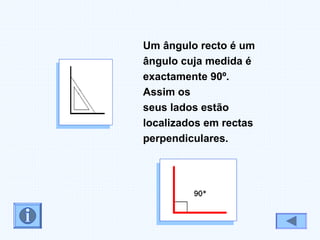
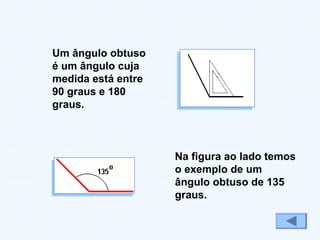
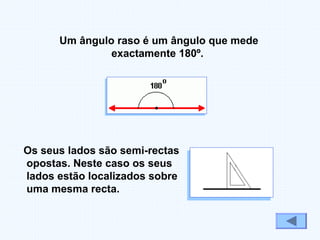
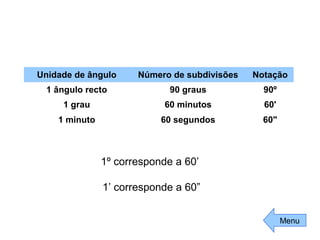
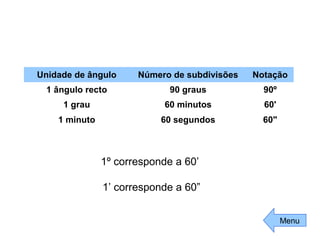
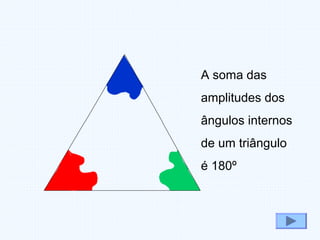
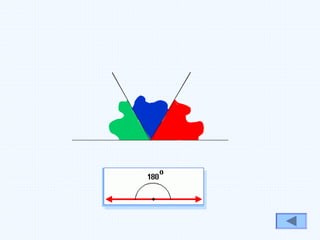
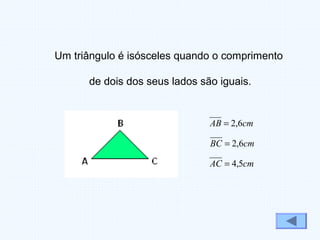
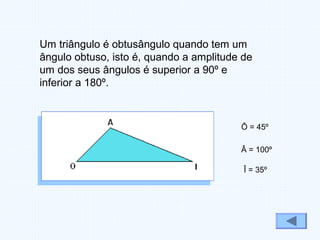
Este documento fornece uma introdução aos conceitos básicos de ângulos e triângulos, incluindo definições históricas de ângulos, tipos de ângulos (agudo, recto, obtuso e raso), classificações de triângulos (equilátero, isósceles e escaleno) e tipos de triângulos (rectângulo, acutângulo e obtusângulo). A soma dos ângulos internos de um triângulo é sempre 180 graus.

1. Tem como objectivo:
Relembrar os jovens sobre
os conceitos de:
“ Ângulos e Triângulos ”

2. Â
ngulos e Triângulos

3. Nota histórica

4.  A Astronomia talvez tenha sido a primeira ciência a
incorporar o estudo de ângulos como uma aplicação da
Matemática.
 O conceito de ângulo aparece, com os gregos, no
estudo de relações envolvendo elementos de um círculo,
arcos e cordas.
 Desde o tempo de Hipócrates e Eudoxo, foram
usadas medidas de ângulos na determinação das
dimensões do planeta Terra, e no cálculo de distâncias
relativas entre o Sol e a Terra.
 Os ângulos eram definidos apenas como ângulos
inferiores a dois rectos, ou seja, menores que 180º.

5. Algumas definições:
Grécia antiga: “ um ângulo é uma deflexão ou
quebra em uma linha recta “.
Euclides: “ um ângulo plano é a inclinação recíproca
de duas rectas que num plano têm um extremo
comum e não estão em prolongamento “.
Actualmente : “ um ângulo é uma porção do plano
limitada por duas semi-rectas com a mesma origem “.

6. Um ângulo não depende do comprimento dos seus
lados mas da abertura que apresenta, ou seja, da
sua amplitude.
Os lados de um ângulo são duas
semi-rectas ( OA e OB ).
A origem das duas semi-rectas designa-se por vértice.
O vértice do ângulo é o ponto O.
Em linguagem matemática, a amplitude do ângulo BOA
escreve-se BÔA.

7. Alguns ângulos especiais
Amplitudes de um ângulo
Triângulos
Sair
EXERCÍCIOSEXERCÍCIOS
EXERCÍCIOSEXERCÍCIOS

8. Não se sabe ao certo quais as razões pelas quais, foi escolhido o
número 360 para se dividir a circunferência, sabe-se apenas que o
número 60 é um dos menores números menores do que 100 que
possui uma grande quantidade de divisores distintos, a saber: 1, 2,
3, 4, 5, 6, 10, 12, 15, 20, 30, 60, razão forte pela qual este número
tenha sido adoptado.
A unidade mais utilizada para medir a amplitude de um ângulo é o
grau (º).
O grau obtém-se pela divisão da circunferência em 360 partes iguais.

9. Para medir a amplitude de um ângulo
usa-se um transferidor
A amplitude dos ângulos é
indicada em graus

10. Cada divisão representa um ângulo de um grau.
tendo a notação de um pequeno o colocado como
expoente do número. Exemplo: 1º.
Em problemas reais, os ângulos nem sempre
possuem medidas associadas a números inteiros,
assim precisamos usar outras unidades menores
como minutos e segundos. A notação para 1
minuto é 1' e a notação para 1 segundo é 1".

11. 1º corresponde a 60’
1’ corresponde a 60”
Unidade de ângulo Número de subdivisões Notação
1 ângulo recto 90 graus 90º
1 grau 60 minutos 60'
1 minuto 60 segundos 60"
Menu

12. Menu

13. Um ângulo agudo é
aquele cuja amplitude é
inferior a um ângulo
recto, ou seja, a sua
amplitude é maior do que
0º e menor do que 90º.

14. Um ângulo recto é um
ângulo cuja medida é
exactamente 90º.
Assim os
seus lados estão
localizados em rectas
perpendiculares.

15. O ângulo recto (90º) é provavelmente o
ângulo mais importante, pois o mesmo
é encontrado em inúmeras aplicações
práticas, como no encontro de uma
parede com o chão, os pés de uma
mesa em relação ao seu tampo, caixas
de papelão, esquadrias de janelas,
etc...

16. Na figura ao lado temos
o exemplo de um
ângulo obtuso de 135
graus.
Um ângulo obtuso
é um ângulo cuja
medida está entre
90 graus e 180
graus.

17. Os seus lados são semi-rectas
opostas. Neste caso os seus
lados estão localizados sobre
uma mesma recta.
Um ângulo raso é um ângulo que mede
exactamente 180º.

18. Os seus lados são duas semi-rectas
coincidentes e que ocupa todo o plano.
Um ângulo giro é um ângulo que mede 360 graus.

19. Para verificar se já sabes
MÚLTIPLA 1MÚLTIPLA 1 MÚLTIPLA 2MÚLTIPLA 2
Menu

20. 1º corresponde a 60’
1’ corresponde a 60”
Unidade de ângulo Número de subdivisões Notação
1 ângulo recto 90 graus 90º
1 grau 60 minutos 60'
1 minuto 60 segundos 60"
Menu

21. 1º corresponde a 60’
1’ corresponde a 60”
Unidade de ângulo Número de subdivisões Notação
1 ângulo recto 90 graus 90º
1 grau 60 minutos 60'
1 minuto 60 segundos 60"
Menu

22. Triângulos

23. Como se classificam os triângulos ?
Como se classificam os triângulos ?
O que é um triângulo ?
O que é um triângulo ?

24. Formado por:
 três lados;
 três vértices;
 três ângulos.
Um triângulo é um polígono fechado.

25. A soma das
amplitudes dos
ângulos internos
de um triângulo
é 180º

27. Menu

28. • Triângulo Equilátero;
• Triângulo Isósceles
• Triângulo Escaleno.

29. cmAB 4,2=
cmBC 4,2=
cmAC 4,2=
Um triângulo é equilátero quando o comprimento
de todos os seus lados são iguais.

30. Um triângulo é isósceles quando o comprimento
de dois dos seus lados são iguais.
cmAB 6,2=
cmBC 6,2=
cmAC 5,4=

31. Um triângulo é escaleno quando o comprimento de
todos os seus lados são diferentes.
cmAB 7,1=
cmBC 5,3=
cmAC 1,4=

32. •Triângulo Rectângulo;
•Triângulo Acutângulo e
•Triângulo Obtusângulo.

33. CÔA = 90º
Um triângulo é rectângulo quando um dos seus
ângulos é recto, isto é, a amplitude de um dos
seus ângulos é de 90º

34. Falar em triângulos é falar de Pitágoras (filósofo grego sec V
a.C.).
Consta-se que Pitágoras andava a passear num jardim
quando observou que a soma das áreas dos quadrados
construídos sobre os lados menores de um triângulo
rectângulo era igual à área do quadrado construído sobre o
lado maior.

35. Um triângulo é acutângulo quando tem todos os
ângulos agudos, isto é, quando a amplitude de
qualquer dos seus ângulos é inferior a 90º.
 = 60º
Ô = 75º
Î = 45º

36. Um triângulo é obtusângulo quando tem um
ângulo obtuso, isto é, quando a amplitude de
um dos seus ângulos é superior a 90º e
inferior a 180º.
Ô = 45º
 = 100º
Î = 35º

37. MÚLTIPLA 4MÚLTIPLA 4MÚLTIPLA 3MÚLTIPLA 3
Para verificar se já sabes
Menu