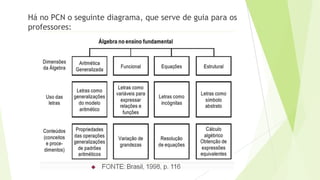
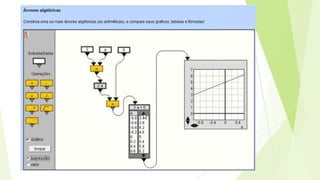
O documento discute como introduzir a linguagem algébrica no ensino, propondo o uso de jogos como o Jogo do Alvo, Bingo Algébrico e máquinas algébricas. Também apresenta uma metodologia de aula com jogos em cinco momentos: familiarização, reconhecimento das regras, jogar para garantir regras, intervenção pedagógica e registro.

1. Expressões Algébricas
Frederico Alindo Gonçalves da Silva
Priscila Cristina de Souza
Sarah Cristina Lemos Nogueira
São José dos Campos
24 de abril de 2013

2. Expressões Algébricas
 Como deveria ser feita a introdução à
linguagem algébrica?
 Metodologia de Aula
 Jogos
Máquinas algébricas
Jogo do Alvo
Bingo Algébrico

3. Como deveria ser feita a introdução à
linguagem algébrica?
 O atual ensino da matemática esta afastado da
realidade da maioria dos alunos.
 Parte deles resolvem expressões algébricas
mecanicamente e não sabem porque chegaram no
resultado ou entendem a resolução do problema.
 E poucos fazem associações com os
conhecimentos adquiridos em seu cotidiano.

4. Charbonneau (1996, p. 34) diz que a álgebra seria “[...] um
caminho para manipular relações”.
Usiskin (1997) divide a álgebra em diferentes subconceitos:
 aritmética generalizada
 estudos de procedimentos para resolução de problemas;
 estudo de relações entre quantidades;
 o estudo de estruturas e propriedades
O PCN de 1998 alerta sobre a importância dada no cálculo
algébrico e das equações. Não realizando assim o
desenvolvimento das diferentes competências do raciocínio de
natureza algébrica.

5. Há no PCN o seguinte diagrama, que serve de guia para os
professores:

6. Metodologia de Aula
 Familiarização dos alunos com o material do jogo: Os jogadores
conhecem o jogo e seus componentes, como tabuleiro, peões, dados ou fichas
e simula jogadas possíveis.
 Reconhecimento das regras: É apresentado às regras, ditas pela
professora ou lidas pelo próprio aluno.
 O “jogo pelo jogo”: Jogar para garantir regras. Nesse momento os
estudantes deverão jogar verificando se entenderam corretamente.
É proposto utilização de jogos em uma sequencia didática para a
iniciação algébrica. Para tanto Grando (2004) definiu os momentos do
jogo:

7.  Intervenção pedagógica verbal: O professor provoca o
aluno, observando-o e questionando-o, para que ele analise suas jogadas
garantindo a relação existente entre o jogo e os conceitos matemáticos.
 Registro do jogo: O estudante registra pontos, cálculos e seus
procedimentos. O professor identifica a construção de estratégias, de
jogadas erradas, compreensão e raciocínio do aluno.
 Intervenção escrita: O professor problematiza as situações ocorridas
no jogo, propondo questões que apareceram ou não no jogo. Pode ser
proposto pelo professor ou pelos alunos.
 Jogar com “competência”: Os alunos jogam novamente o jogo, mas
agora considera os passos anteriores, para refletir se sua estratégia
anterior era a melhor e de fato jogar com competência.

8. Máquinas algébricas
 Podem contribuir para o aprendizado do significado das
“letras”.
 O processo de resolução do problema é esquematizado usando
a “caixa branca” como espaço a ser ocupado por números que
correspondem a situações, tem-se nesse procedimento o uso da ideia
de variável.
 O aluno não precisa se preocupar em efetuar cálculos, sendo
apenas necessário que identifique as etapas de resolução do
problema.
 A habilidade do aluno para representar as etapas do problema
pode ser o início da demonstração do pensamento algébrico .

10. Jogo do Alvo
Objetivo: Promove a interação entre os alunos e exercita de forma
motivadora o cálculo de valores numéricos como consequência da contagem
de pontos, as operações com polinômios são sugeridas naturalmente.
Instruções:
 O aluno deve construir em papel cartão um alvo colorido com 30 cm de diâmetro.
Sobre esse alvo são jogados 12 feijões onde o jogador deve anotar a quantidade de feijões
que caiu em cada cor.
 Após todas as jogadas o professor pede que se use uma única letra para representar
cada cor e reescreva os resultados obtidos nas cinco rodadas.
 Obedecendo a valores estipulados pelo professor para as cores, o aluno soma seus
pontos.

11. EXEMPLO:
 1ª RODADA :
5 brancos,0 pretos,5 azuis,2
vermelhos e 0 amarelos
 2ª RODADA:
3b,3p,4a,0v e 2m
 3ª RODADA:
5b,5p,0a,1v e 1m
 4ª RODADA:
1b,4p,4a,1v e 2 m
 5ª RODADA :
4b,0p,0a,4v,4m
 TOTAL:
18b,12p,13a,8v,8m

12. Bingo Algébrico
 Objetivo: O jogo ressalta a fatoração e a aplicação de produtos
notáveis na resolução de problemas, que depende de uma identificação
inicial da expressão algébrica. O aluno precisa perceber que a expressão
algébrica presente na solução pode ser fatorada ou escrita de outra
forma, por ser um produto notável. É uma forma de aprender a
identificar as expressões algébricas que podem ser fatoradas ou que são
produtos notáveis. O aluno deve reconhecer as expressões tanto quando
na forma fatorada, assim como na forma de produtos notáveis.

13. Instruções:
2º1º
 Faz-se fichas de cada linha da primeira e da
segunda fileira, coloca-se em envelopes
separados, chamados respectivamente de 1º e
2º, para sorteio.
 Os alunos formam duplas e cada dupla
aleatoriamente retira cinco tiras do 2 envelope.
 O professor retira aleatoriamente do 1º envelope
uma tira e passa para a lousa a expressão.
 Em 30 segundos os alunos desenvolvem a
expressão e verificam se possuem a resposta
compatível, e anotam,sem se manifestar.
O processo se repetirá até que se obtenha cincos expressões que correspondam com as respostas
daquelas passadas pelo professor na lousa. Quando isso ocorrer, a dupla de alunos gritará bingo; após
a verificação das expressões, se corretas será proclamado um vencedor.

14. Referências Bibliográficas
 Atividades de laboratório de Ensino de matemática-Universidade sem fronteiras- Maringá 2009 - DISPONÍVEL EM:
http://jucienebertoldo.files.wordpress.com/2012/11/atividades-de-laboratc3b3rio-de-matemc3a1tica-2.pdf. Data de
acesso: 21/04/2013.
 Búrigo, E. Z.; Gravina, M.A.; Basso, M.V.A.; Garcia, V.C.V. . Matemática na escola: novos conteúdos, novas
abordagens .1º ed. Local de publicação: Porto Alegre: Editora da UFRGS, 2012.301 p. Série educação a distância.
 Software máquina algébrica – Disponível em: www.edumatec.mat.ufrgs.br/.../arvoresalgebricas.htm - Data de acesso:
23/04/2013.
 PANOSSIAN, M.L.Manifestações do pensamento e da linguagem algébrica de estudantes: indicadores para a
organização do ensino. 2008. Dissertação (Mestrado em Educação) -Faculdade de Educação, Universidade de São
Paulo, São Paulo, 2008. Disponível em: http://www.teses.usp.br/teses/disponiveis/48/48134/tde-23012009-143154/.
Data de acesso: 21/04/2013.
 RAUPP, A.D. Educação Matemática: processos interativos em situações de jogo no ensino fundamental. Dissertação
(Mestrado em Educação). Universidade Passo Fundo,2009. Disponível em:
http://www.ppgedu.upf.br/index.php?option=com_docman&task=doc_download&gid=71. Data de acesso: 21/04/2013.