O documento discute conceitos básicos de trigonometria, incluindo:
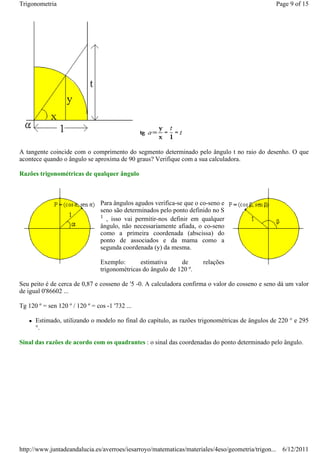
1) Definições de seno, cosseno e tangente de um ângulo agudo em um triângulo retângulo.
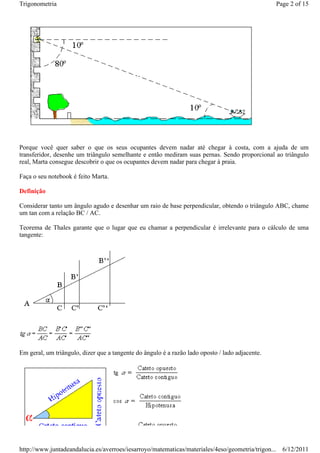
2) Exemplos de como estimar distâncias usando razões trigonométricas, como a distância da Terra à Lua.
3) Propriedades importantes como o Teorema Fundamental e relações entre ângulos complementares.