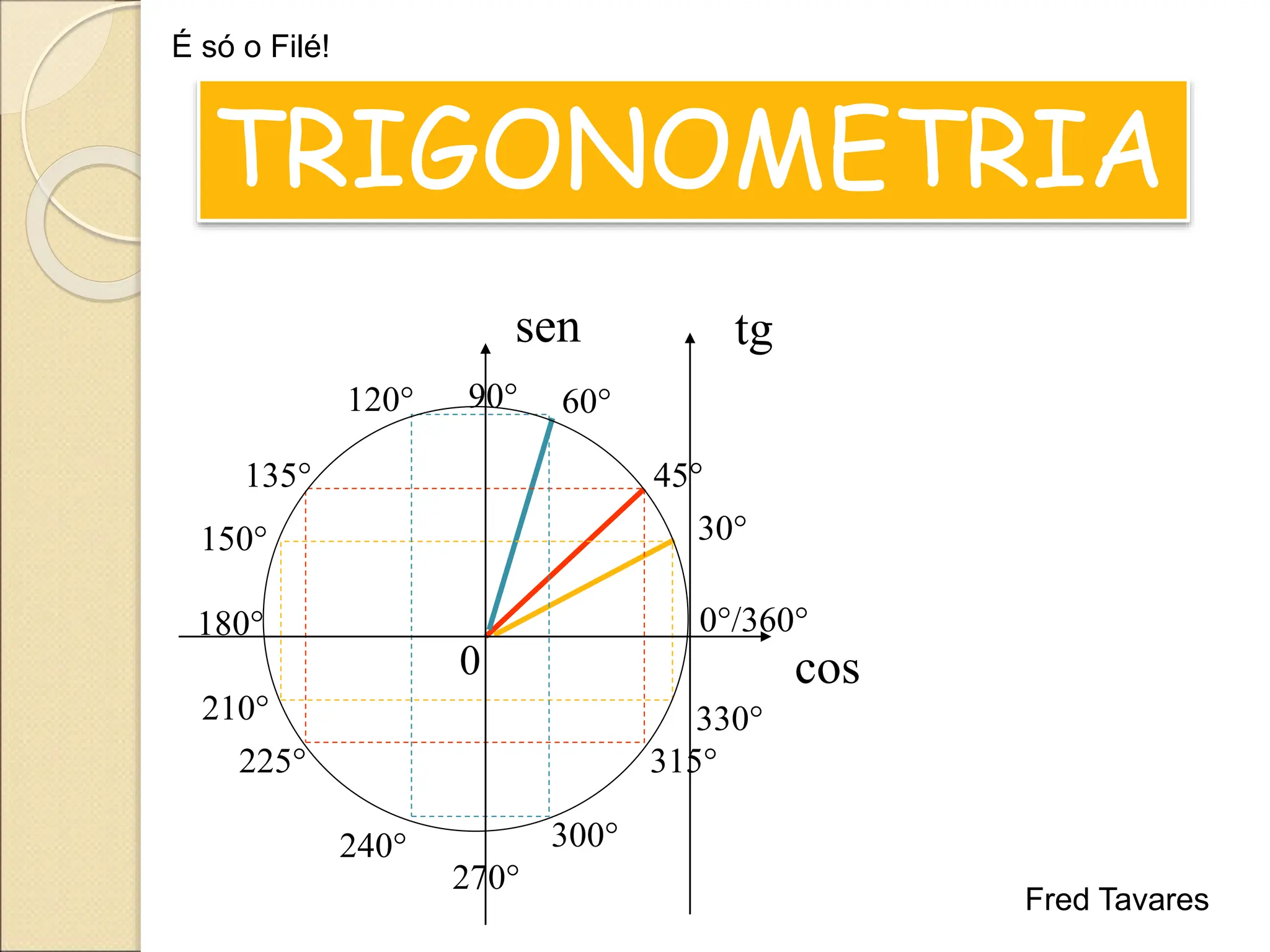
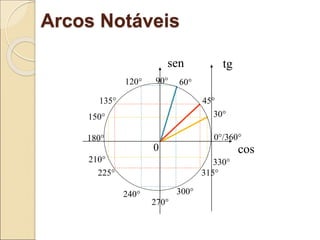
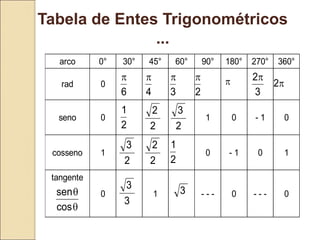
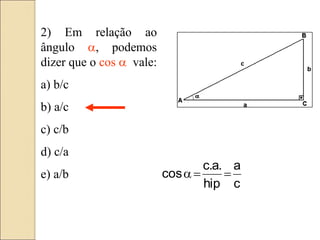
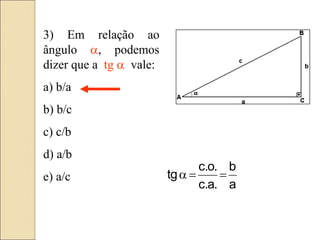
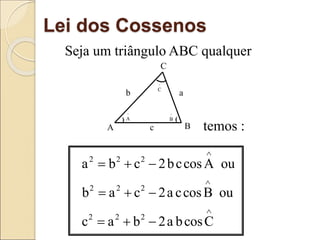
O documento discute conceitos de trigonometria, incluindo relações no triângulo retângulo, o teorema fundamental da trigonometria e funções trigonométricas. Apresenta exemplos práticos e aplicações em mecânica e medições de alturas utilizando tangentes. Inclui tabelas de valores trigonométricos e questões para revisão do conteúdo.

1. 30°
150°
210° 330°
45°
135°
225° 315°
60°
120°
240° 300°
cos
sen
0
tg
90°
180°
270°
0°/360°
TRIGONOMETRIA
É só o Filé!
Fred Tavares

2. 30°
150°
210° 330°
45°
135°
225° 315°
60°
120°
240° 300°
cos
sen
0
tg
90°
180°
270°
0°/360°
TRIGONOMETRIA
É só o Filé!
Fred Tavares

3. Teorema Fundamental da
Trigonometria
1
cos
sen 2
2





4. Demonstração ...
)θ
1 cos
sen
1
-1
-1
0
sen θ
cos θ
θ
·

5. Continuação...
)θ
1 cos
sen
1
-1
-1
0
sen θ
cos θ
1

6. Continuação...
)θ
sen θ
cos θ
1
Utilizando o teorema de
Pitágoras h2 = c2 + c2, temos :
1
cos
sen 2
2




C M P Q D

7. Relações Trigonométricas no
Triângulo Retângulo
)θ
Hipotenusa

8. Continuação ...
Cotangente de θ
Secante de θ
Cossecante de θ
Tangente de θ
Cosseno de θ
Seno de θ
Relação no Triângulo
Retângulo
Ente
Trigonométrico
HI
CO
sen 

HI
CA
cos 

CO
HI
sen
1
sec
cos 



CA
CO
tg 

CA
HI
cos
1
sec 



CO
CA
tg
1
g
cot 




9. Na Circunferência
Trigonométrica
)θ
cos
sen
0
sen θ
cos θ
·
tg
tg θ

10. Continuação ...
)θ
0
·
cotg
cotg θ
secante θ
cossec θ

11. Arcos Notáveis
30°
150°
210° 330°
45°
135°
225° 315°
60°
120°
240° 300°
cos
sen
0
tg
90°
180°
270°
0°/360°

12. arco 0° 30° 45° 60° 90° 180° 270° 360°
rad 0
6

4

3

2
 
3
2

2
seno 0
2
1
2
2
2
3
1 0 - 1 0
cosseno 1
2
3
2
2
2
1
0 - 1 0 1
tangente


cos
sen 0
3
3
1 3 - - - 0 - - - 0
Tabela de Entes Trigonométricos
...

13. Vamos pensar . . .
?

14. Que tal fazermos um teste para verificação do
que foi apresentado?
Observem a figura ao lado
1) Em relação ao
ângulo a, podemos
dizer que o sen a vale:
a) b/c
b) a/c
c) c/b
d) c/a
e) a/b
c
b
hip
.
o
.
c
sen 

a

15. 2) Em relação ao
ângulo a, podemos
dizer que o cos a vale:
a) b/c
b) a/c
c) c/b
d) c/a
e) a/b
c
a
hip
.
a
.
c
cos 

a

16. 3) Em relação ao
ângulo a, podemos
dizer que a tg a vale:
a) b/a
b) b/c
c) c/b
d) a/b
e) a/c
a
b
.
a
.
c
.
o
.
c
tg 

a

17. 4) Em relação ao
ângulo a, podemos
dizer que a cotg a
vale:
a) b/a
b) b/c
c) c/b
d) a/b
e) a/c b
a
.
o
.
c
.
a
.
c
g
cot 

a

18. 5) Em relação ao
ângulo a, podemos
dizer que tg a .cotg a
vale:
a) 1/a
b) 1/c
c) 1/b
d) 0
e) 1 1
.
o
.
c
.
a
.
c
.
.
a
.
c
.
o
.
c
g
cot
.
tg

a
a

19. 6) Se a = 3b, podemos
dizer então, que
sen2 a + cos2 a vale:
a) b2 / a2
b) 9c2 / b2
c) 0
d) 1
e) (c2 + b2) / 9a2
Pelo teorema fundamental da
trigonometria, temos que:
sen2  + cos2  = 1

20. 7) Em relação ao
ângulo a, podemos
dizer que sec2a - 1
vale:
a) tg2a
b) cotg2a
c) - 1
d) 0
e) 1
 
a

a









a

a
a

a
2
2
2
2
cos
1
sec
cos
1
sec
o
log
,
cos
1
sec
a


a

a
a

a
a



a


a 2
2
2
2
2
2
2
2
tg
1
sec
cos
sen
cos
cos
1
1
cos
1
1
sec
a


a

a

a
2
2
2
2
cos
1
sen
1
cos
sen
a


a 2
2
tg
1
sec

21. 8) Em relação ao
ângulo a, podemos
dizer que cossec2a - 1
vale:
a) tg2a
b) cotg2a
c) - 1
d) 0
e) 1  
a

a









a

a
a

a
2
2
2
2
sen
1
sec
cos
sen
1
sec
cos
o
log
,
sen
1
sec
cos
a


a

a
a

a
a



a


a 2
2
2
2
2
2
2
2
g
cot
1
sec
cos
sen
cos
sen
sen
1
1
sen
1
1
sec
cos
a


a 2
2
g
cot
1
sec
cos

22. 9) Se sen a  b/c,
então, calculando o
valor de
chegaremos a:
a) a/c
b) b/c
c) a/b
d) b/a
e) 1








a

a

a

cos
1
1
.
)
cos
1
(
.
g
cot
y
Procure sempre partir da relação fundamental
Resposta na outra folha

23. 







a

a
a

a
a









a

a

a

cos
1
cos
.
)
cos
1
(
.
sen
cos
y
cos
1
1
.
)
cos
1
(
.
g
cot
y a


a

a

a
2
2
2
2
cos
1
sen
1
cos
sen
 
)
cos
cos
1
(cos
.
sen
1
y
1
cos
.
)
cos
1
(
.
sen
1
y
2
a

a


a
a


a
a

a

)
cos
1
(
.
sen
1
y 2
a

a

a
a
 2
sen
.
sen
1
y
c
b
y
sen
y

a


24. Voltando
para a parte teórica...

25. Lei dos Senos
Seja um triângulo ABC qualquer
temos :





C
sen
c
B
sen
b
A
sen
a
) (
^
A
^
C
^
B
A B
C
a
c
b

26. Lei dos Cossenos
Seja um triângulo ABC qualquer
temos :












C
cos
b
a
2
b
a
c
ou
B
cos
c
a
2
c
a
b
ou
A
cos
c
b
2
c
b
a
2
2
2
2
2
2
2
2
2
) (
^
A
^
C
^
B
A B
C
a
c
b

27. Gráficos das funções
trigonométricas
Senóide
sen
x
y
x
•
•
•
•
•
•
•
•
•
•
0° 540
°
720
°
450
°
630
°
360
°
270
°
180
°
-180° -90°
•
90
°
1
-
1

28. Cossenóide
cos
x
y
x
•
•
• •
•
•
•
•
•
•
•
0°
540°
720°
450
°
630°
360
°
270
°
180
°
-180°
-90° 90
°
1
-
1

29. Tangente
tg x
y
x
• • •
•
• • • • •
0° 360
°
-90° 90°
180°
270° 450
°
540°
630°

30. Cossecante
y
x
• •
•
•
•
•
•
• • •
0° 540° 720°
450
°
630°
360
°
270
°
180
°
-180° -90°
• 90°
1
-
1
cossec
x

31. Secante
•
•
• •
•
•
• •
•
•
•
0°
540°
720°
450
°
630°
360
°
270
°
180
°
-180°
-90° 90°
sec
x
y
x
1
-
1

32. Continuação ...
cotg x
y
x
• • •
•
• • • • •
0° 360
°
90°
180°
270° 450
° 540°
630°
720°

33. Trigonometria
Algumas Aplicações

34. Parte Prática
O exemplo clássico da Sombra
Para que possamos medir
(aproximadamente) a altura de um prédio,
sem a necessidade de subir ao terraço, ou
utilizar equipamentos sofisticados, seria
necessário somente 2 elementos.
São eles: uma distância
um ângulo
Observe a seguir . . .

35. h
d
.
tg
d
h
tg
.
a
.
c
.
o
.
c
tg

a

a


a
portanto: a
 tg
.
d
h
Conhecendo a distância d que vale 50 metros e o
ângulo a que vale 30°, podemos dizer então que:
metros
8675
,
28
h
9
5773502691
,
0
.
50
h
30
tg
.
50
h
tg
.
d
h




a


36. Exemplo 01.
Uma rampa com inclinação constante, (como
a que existe em Brasília) tem 6 metros de
altura na sua parte mais elevada. Um
engenheiro começou a subir, e nota que após
ter caminhado 16,4 metros sobre a rampa está
a 2,0 metros de altura em relação ao solo. Será
que este engenheiro somente com esses dados
e uma calculadora científica conseguiria
determinar o comprimento total dessa rampa e
sua inclinação em relação ao solo?

37. Como poderíamos resolver essa situação?
Como sugestão, faremos um “desenho” do que
representa essa situação.
Observemos:
6 metros
16,4 metros
2 metros

Comprimento total da rampa
solo

38. 6 metros
16,4 metros
2 metros

Observemos o triângulo retângulo em destaque . . .
 2 metros
16,4 metros
hip c.o.
c.a.
Temos em relação
ao ângulo :
hip = 16,4 metros
c.o. = 2 metros

39.  2 metros
16,4 metros
hip c.o.
c.a.
Como:
hip = 16,4 metros
c.o. = 2 metros
12
1219512195
,
0
4
,
16
2
hip
.
o
.
c
sen 



Obs.: quando dizemos que arcsen a = 1/2 , podemos
transformar essa igualdade em uma pergunta: “qual é o arco,
cujo seno vale 1/2?”, a resposta seria dizer que a = 30°.

40. Em nosso exercício, chegamos a conclusão
que:
sen  = 0,121951219512, logo podemos encontrar
o ângulo , com o auxílio da calculadora que
normalmente utiliza as funções ASIN ou SIN-1,
então, devemos digitar 0,121951219512 e a opção
acima de sua calculadora.
Se o processo foi realizado corretamente,
deverá ser encontrado o valor 7,00472640907, que
iremos considerar como aproximadamente 7°.
Encontramos assim, a inclinação da rampa!

41. 2
,
49
12
1219512195
,
0
6
7
sen
6
sen
o
.
c
hip
sen
o
.
c
hip
.
o
.
c
hip
.
sen
hip
.
o
.
c
sen














6 metros
  7
Notamos que os triângulos abaixo são semelhantes,
portanto, podemos dizer que  é válido para ambos
 2 metros
16,4 metros
hip c.o.
c.a.
Como:
Chegamos a conclusão que o
comprimento total da rampa é 49,2 metros

42. Exemplo 2
Mecânica Geral
ou Trigonometria?

43. Em relação ao sistema de
forças
representado na figura, onde
F1 = 20N,
F2 = 100N, F3 = 40N e
F4 = 10N, você
seria capaz de determinar a
intensidade da resultante do
sistema e o ângulo que essa
resultante forma com o eixo
das abscissas (x)?
Os conceitos trigonométricos aparecem com muita freqüência no estudo da
Física, Topografia, Astronomia e de muitos outros assuntos.
Abaixo segue um problema CLÁSSICO de física e trigonometria

44. Em primeiro lugar, teremos que fazer as projeções de 2
F

nos eixos das abscissas e das
ordenadas, obtendo assim, respectivamente os componentes )
x
(
2
F

e )
y
(
2
F

.
Analogamente, encontraremos as projeções de 3
F

, encontrando os componentes )
x
(
3
F

e )
y
(
3
F

.

45. A resultante relativa ao eixo das abscissas 




 
)
x
(
R
é obtida
da seguinte maneira:
)
x
(
3
1
)
x
(
2
)
x
( F
F
F
R
























a










a
60
cos
.
F
F
F
F
.
60
cos
F
F
60
cos
.
hip
a
.
c
cos
45
cos
.
F
F
F
F
.
45
cos
F
F
45
cos
.
hip
a
.
c
cos
Como
3
)
x
(
3
)
x
(
3
3
3
)
x
(
3
2
)
x
(
2
)
x
(
2
2
2
)
x
(
2













N
20
F
5
,
0
.
40
60
cos
.
F
F
N
70
F
70
,
0
.
100
45
cos
.
F
F
to
tan
Por
)
x
(
3
3
)
x
(
3
)
x
(
2
2
)
x
(
2
)
x
(
3
1
)
x
(
2
)
x
( F
F
F
R







N
70
R
20
20
70
R
)
x
(
)
x
(







46. A resultante relativa ao eixo das abscissas 




 
)
y
(
R
é obtida
da seguinte maneira:
)
y
(
3
4
)
y
(
2
)
y
( F
F
F
R
























a










a
60
sen
.
F
F
F
F
.
60
sen
F
F
60
sen
.
hip
o
.
c
sen
45
sen
.
F
F
F
F
.
45
sen
F
F
45
sen
.
hip
o
.
c
sen
Como
3
)
y
(
3
)
y
(
3
3
3
)
y
(
3
2
)
y
(
2
)
y
(
2
2
2
)
y
(
2













N
4
,
34
F
86
,
0
.
40
60
sen
.
F
F
N
70
F
70
,
0
.
100
45
sen
.
F
F
to
tan
Por
)
y
(
2
3
)
y
(
3
)
y
(
2
2
)
y
(
2
)
y
(
3
4
)
y
(
2
)
y
( F
F
F
R







N
6
,
25
R
4
,
34
10
70
R
)
y
(
)
y
(







47. 












N
F
sen
F
F
N
F
sen
F
F
to
Por
y
y
y
y
4
,
34
86
,
0
.
40
60
.
70
70
,
0
.
100
45
.
tan
)
(
2
3
)
(
3
)
(
2
2
)
(
2
)
y
(
3
4
)
y
(
2
)
y
( F
F
F
R







N
6
,
25
R
4
,
34
10
70
R
)
y
(
)
y
(







48. Colocando )
x
(
R

e )
y
(
R

, nos eixos das abscissas e das
ordenadas, respectivamente,
Percebemos que a figura formada pelas forças é um
triângulo retângulo, em que sua hipotenusa é a Força
Resultante

R , )
x
(
R

é o cateto adjacente a a e )
y
(
R

o
cateto oposto a a, então, vale o teorema de Pitágoras para
calcularmos o valor de

R .

49.    
N
53
,
74
R
36
,
5555
R
36
,
5555
R
36
,
655
4900
R
6
,
25
70
R
R
R
R
c
c
h
2
2
2
2
2
2
)
y
(
2
)
x
(
2
2
2
2























































Observe que são problemas bem clássicos e resolvidos da mesma forma.

50. Para o cálculo do ângulo a, temos:
3657
,
0
70
6
,
25
R
R
.
a
.
c
.
o
.
c
tg
)
x
(
)
y
(




a 

3657
,
0
tg 
a
Esse é o valor da tangente do ângulo a
Para calcularmos o valor do ângulo a,
temos que encontrar o arctg a, então:


a

a

a
20
3657
,
0
arctg
arctg
Concluímos então que a Resultante N
53
,
74
R

e forma
um ângulo 

a 20 com o eixo x.

51. Mais um Problema Clássico de Vestibular

52. Questão01. Um alpinista muito ágil, percorre um
trajeto passando pelos pontos A e B. Não se sabe ao certo o
que ocorreu, mas ele conseguiu com o material apropriado
chegar a conclusão das medidas abaixo mencionadas. Quando
chega até a árvore ele percebe que o único caminho que o
levará até o ponto C é escalando-a. (a altura da árvore é
representada por h - despreze a largura do tronco)
Se sua velocidade média é de 0,2 m/s, quantos
minutos ele demorou para sair do ponto A e chegar ao ponto
C? ( )
7
,
1
3 

53. Solução:
Resumidamente,
temos o triângulo ao
lado que representa
nosso desafio.
)
II
(
y
.
3
h
y
.
60
tg
h
h
y
.
60
tg
y
h
.
a
.
c
.
o
.
c
60
tg
)
I
(
)
y
20
(
.
3
3
h
)
y
20
(
.
30
tg
h
h
)
y
20
(
.
30
tg
)
y
20
(
h
.
a
.
c
.
o
.
c
30
tg

























54. metros
10
y
y
2
20
y
y
3
20
y
.
3
)
y
20
(
y
.
3
.
3
)
y
20
(
.
3
y
.
3
)
y
20
(
.
3
3
y
.
3
h
)
II
(
)
y
20
(
.
3
3
h
)
I
(


















Igualando o h das equações ( I ) e (II)
Como
metros
17
h
10
.
7
,
1
h
y
.
3
h




55. 30 metros
17 metros para
subir a árvore
17 metros para
descer da árvore
Agora com o valor das medidas temos condição de
determinar quanto ele percorreu do ponto A até o
ponto C, observe:
De A até C ele percorreu 30 + 17 + 17 = 64 metros
v = 0,2 m/s

56. segundos
20
e
utos
min
5
t
ou
utos
min
333
,
5
t
60
segundos
320
t
segundos
320
2
,
0
64
t
V
s
t
s
t
.
V
t
s
V






















Portanto

57. RESUMÃO DE FÓRMULAS
Relações básicas
sen2 α + cos2 α = 1
tan α . cot α = 1
1 + tan2 α = 1 / cos2 α
1 + cot2 α = 1 / sen2 α
Relações com quadrantes
Obs: valores de ângulos em graus. Conversão para radianos:
90 → π/2 180 → π 270 → 3π/2 360 → 2π
sen (90 + α) = + cos α sen (90 − α) = + cos α
sen (180 + α) = − sen α sen (180 − α) = + sen α
cos (90 + α) = − sen α cos (90 − α) = + sen α
cos (180 + α) = − cos α cos (180 − α) = − cos α

58. RESUMÃO DE FÓRMULAS
tag (90 + α) = − cot α tan (90 − α) = + cot α
tan (180 + α) = + tan α tan (180 − α) = − tan α
cot (90 + α) = − tan α cot (90 − α) = + tan α
cot (180 + α) = + cot α cot (180 − α) = − cot α
sen (270 + α) = − cos α sen (270 − α) = − cos α
sen (360 + α) = + sen α sen (360 − α) = − sen α
cos (270 + α) = + sen α cos (270 − α) = − sen α
cos (360 + α) = + cos α cos (360 − α) = + cos α
tan (270 + α) = − cot α tan (270 − α) = + cot α
tan (360 + α) = + tan α tan (360 − α) = − tan α
cot (270 + α) = − tan α cot (270 − α) = + tan α
cot (360 + α) = + cot α cot (360 − α) = − cot α
sen (−α) = − sen α cos (−α) = + cos α
tan (−α) = − tan α cot (−α) = − cot α
sen (α ± k 360) = + sen α cos (α ± k 360) = + cos α
tan (α ± k 180) = + tan α cot (α ± k 180) = + cot α
O símbolo k significa um número inteiro e positivo.

59. RESUMÃO DE FÓRMULAS
Relações com soma / diferença de ângulos
sen (α ± β) = sen α cos β ± cos α sen β
cos (α ± β) = cos α cos β ± sen α sen β
tan (α ± β) = (tan α ± tan β) / (1 ± tan α tan β)
cot (α ± β) = (cot α cot β ± 1) / (cot β ± cot α)
Relações com soma / diferença / produto de funções
sen α + sen β = 2 sen (α + β)/2 . cos (α − β)/2
sen α − sen β = 2 cos (α + β)/2 . sen (α − β)/2
cos α + cos β = 2 cos (α + β)/2 . cos (α − β)/2
cos α − cos β = − 2 sen (α + β)/2 . sen (α − β)/2

60. a sen x + b cos x = √ (a2 + b2) sen (x + φ) onde φ = arctan b/a se
a ≥ 0 ou
φ = arctan b/a ± π se a < 0
tan α ± tan β = sen (α ± β) / (cos α cos β)
cot α ± cot β = sen (β ± α) / (sen α sen β)
sen α sen β = (1/2) cos (α − β) − (1/2) cos (α + β)
sen α cos β = (1/2) sen (α + β) + (1/2) sen (α − β)
cos α cos β = (1/2) cos (α + β) + (1/2) cos (α − β)
tan α tan β = (tan α + tan β) / (cot α + cot β) = − (tan α − tan β) / (cot α − cotβ)
cot α cot β = (cot α + cot β) / (tan α + tan β) = − (cot α − cot β) /(tan α − tan β)
cot α tan β = (cot α + tan β) / (tan α + cot β) = − (cot α − tan β) /(tan α − cot β)
RESUMÃO DE FÓRMULAS

61. Relações diversas
sen α = 2 sen α/2 . cos α/2
cos α = cos2 α/2 − sen2 α/2
tan α = sen α / cos α
cot α = cos α / sen α
sen α = tan α / √(1 + tan2 α)
cos α = cot α / √(1 + cot2 α)
tan α = sen α / √(1 − sen2 α)
cot α = cos α / √(1 − cos2 α)
sen α = √(cos2 α − cos 2α)

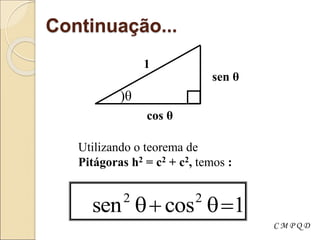
62. Relações diversas
cos α = 1 − 2 sen2 α/2
tan α = √[ (1/cos2 α) − 1 ]
cot α = √[ (1/sen2 α) − 1 ]
sen α = √[ (1 − cos 2α) / 2 ]
cos α = √[ (1 + cos 2α) / 2 ]
tan α = [ √(1 − cos2 α) ] / cos α
cot α = [ √(1 − sen2 α) ] / sen α
sen α = 1 / √(1 + cot2 α)
cos α = 1 / √(1 + tan2 α)
sen 2α = 2 sen α cos α

63. Relações diversas
cos 2α = cos2 α − sen2 α
cos 2α = 2 cos2 α − 1
cos 2α = 1 − 2 sen2 α
tan 2α = 2 tan α / (1 − tan2 α)
tan 2α = 2 / (cot α − tan α)
cot 2α = (cot2 α − 1) / (2 cot α)
cot 2α = (1/2) cot α − (1/2) tan α
sen α/2 = √[ (1 − cos α) / 2 ]
cos α/2 = √[ (1 + cos α) / 2 ]
tan α/2 = sen α / (1 + cos α)
cot α/2 = sen α / (1 − cos α)
tan α/2 = (1 − cos α) / sen α
cot α/2 = (1 + cos α) / sen α
tan α/2 = √[ (1 − cos α) / (1 + cos α) ]

64. Pessoal, espero ter contribuído um pouco mais para o seu sucesso.
Abraços
Fred Tavares
www.nordesttino.com
nordesttino@hotmail.com