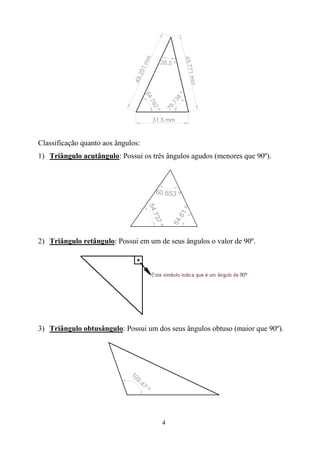
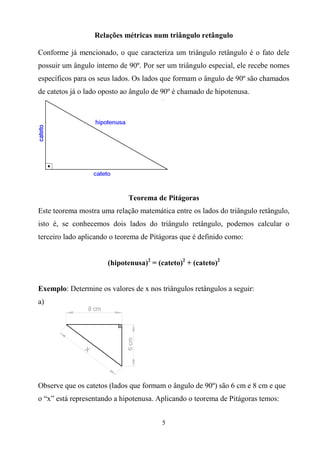
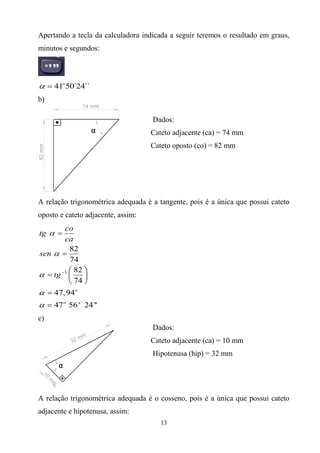
1) O documento apresenta conceitos fundamentais de geometria para engenharia, incluindo definições de polígonos, triângulos e suas classificações, além de relações métricas e trigonométricas em triângulos retângulos e não retângulos. 2) São explicados em detalhe o Teorema de Pitágoras, Leis dos Senos e Cosenos, cálculo de áreas e volumes de figuras geométricas como polígonos e círculos. 3) Vários exemplos numéricos são fornecidos

1. MATEMÁTICA FUNDAMENTAL PARA
INICIANTES DE ENGENHARIA
GEOMETRIA
Prof. Luciano Galdino

2. SUMÁRIO
Noções de Geometria........................................................................................................ 02
Polígono................................................................................................................................. 02
Triângulo.............................................................................................................................. 03
Relações métricas num triângulo retângulo ........................................................... 05
Teorema de Pitágoras...................................................................................................... 05
Relações trigonométricas num triângulo retângulo.............................................. 07
Relações trigonométricas num triângulo qualquer............................................... 14
Lei dos senos........................................................................................................................ 14
Lei dos cossenos ................................................................................................................. 17
Área dos principais polígonos....................................................................................... 19
Perímetro dos polígonos.................................................................................................. 21
Circunferência e círculo.................................................................................................. 21
Comprimento da circunferência (perímetro).......................................................... 22
Área de um círculo............................................................................................................ 23
Radiano................................................................................................................................. 24
Volume de alguns sólidos geométricos....................................................................... 25

3. 2
Noções de Geometria
A geometria está muito presente nas aplicações em Engenharia e, portanto, o seu
estudo apresenta uma grande importância. Em diversos projetos de Engenharia
utilizam-se conceitos de geometria, sendo os de maior destaque as aplicações com
triângulos e circunferências, os cálculos de área e os cálculos de volume.
Polígono
É uma figura geométrica fechada e formada por segmentos de reta. Pode ser
classificado segundo a sua quantidade de segmentos de retas (lados), sendo que
alguns deles recebem nomes especiais, conforme pode ser observado na tabela 1.
Número de
lados
Nomes
3 Triângulo
4 Quadrilátero
5 Pentágono
6 Hexágono
7 Heptágono
8 Octógono
9 Eneágono
10 Decágono
11 Undecágono
12 Dodecágono
15 Pentadecágono
20 Icoságono
Tabela 1: Nomenclatura dos polígonos especiais.
Os demais polígonos não recebem nomes especiais, assim, caso ele tenha 13 lados,
será chamado de polígono de 13 lados, se tiver 21 lados, será chamado de polígono
de 21 lados, e assim sucessivamente.
Os polígonos mais utilizados na Engenharia são os triângulos e os quadriláteros
(em especial o quadrado e o retângulo).

4. 3
Triângulo
O triângulo, por ser o polígono mais simples, é a figura geométrica mais estudada
na geometria. Eles podem ser classificados segundo os seus lados e também
segundo os seus ângulos.
Classificação quanto aos lados:
1) Triângulo equilátero: Possui os três lados iguais e, consequentemente, os três
ângulos iguais.
Em qualquer triângulo, a soma de seus ângulos internos deve ser igual a 180º,
assim, o triângulo equilátero possui três ângulos de 60º.
2) Triângulo isósceles: Possui dois lados iguais e, consequentemente, dois
ângulos iguais.
3) Triângulo escaleno: Possui todos os lados diferentes e consequentemente os
três ângulos diferentes.

5. 4
Classificação quanto aos ângulos:
1) Triângulo acutângulo: Possui os três ângulos agudos (menores que 90º).
2) Triângulo retângulo: Possui em um de seus ângulos o valor de 90º.
3) Triângulo obtusângulo: Possui um dos seus ângulos obtuso (maior que 90º).

6. 5
Relações métricas num triângulo retângulo
Conforme já mencionado, o que caracteriza um triângulo retângulo é o fato dele
possuir um ângulo interno de 90º. Por ser um triângulo especial, ele recebe nomes
específicos para os seus lados. Os lados que formam o ângulo de 90º são chamados
de catetos já o lado oposto ao ângulo de 90º é chamado de hipotenusa.
Teorema de Pitágoras
Este teorema mostra uma relação matemática entre os lados do triângulo retângulo,
isto é, se conhecemos dois lados do triângulo retângulo, podemos calcular o
terceiro lado aplicando o teorema de Pitágoras que é definido como:
(hipotenusa)2
= (cateto)2
+ (cateto)2
Exemplo: Determine os valores de x nos triângulos retângulos a seguir:
a)
Observe que os catetos (lados que formam o ângulo de 90º) são 6 cm e 8 cm e que
o “x” está representando a hipotenusa. Aplicando o teorema de Pitágoras temos:

7. 6
2 2 2
2 2 2
2
2
6 8
36 64
100
100
10
hip cat cat
x
x
x
x
x cm
 
 
 

 

Observe que na penúltima linha da resolução foram colocados os sinais de +/-, pois
(-10)2
=100 e (+10)2
=100, isto é, existem duas respostas uma positiva e a outra
negativa, mas nesse caso, sabemos que é impossível uma medida de comprimento
ter valor negativo, por isso que a resposta final é 10 cm positivo. Portanto, daqui
por diante, iremos considerar somente o resultado positivo.
b)
Neste exemplo nós temos a hipotenusa igual a 50 mm, um dos catetos igual a 30
mm e o “x” está representando o outro cateto. Aplicando o teorema de Pitágoras
temos:
2 2 2
2 2 2
2
2
2
50 30
2500 900
2500 900
1600
1600
40
40
hip cat cat
x
x
x
x
x
x ou
x mm
 
 
 
 

 



8. 7
Nesses tipos de cálculos as funções que utilizamos na calculadora científica são:
Tecla para elevar ao quadrado:
Tecla para extrair a raiz quadrada:
Relações trigonométricas num triângulo retângulo
Conhecendo o valor de um lado e de um ângulo (exceto o de 90º que já é
conhecido) de um triângulo retângulo, podemos calcular os valores dos outros
lados deste triângulo através das relações trigonométricas, assim como, podemos
calcular um ângulo de referência conhecendo-se dois lados de um triângulo
retângulo também pelas relações trigonométricas.
O primeiro passo para trabalhar com as relações trigonométricas num triângulo
retângulo é verificar qual o ângulo deste triângulo que será utilizado e, a partir dele
nomear os catetos, isto é, o lado do triângulo que estiver oposto a esse ângulo é
denominado cateto oposto (co) e o lado que está formando esse ângulo, isto é, que
é vizinho do ângulo, é chamado de cateto adjacente. Já a hipotenusa é sempre o
lado oposto ao ângulo de 90º do triângulo.
Assim, do triângulo a seguir temos:
a = hipotenusa;
b = cateto oposto ao ângulo ;
c = cateto adjacente ao ângulo .

9. 8
Caso seja utilizado o outro ângulo como referência, altera-se apenas o cateto
oposto e o adjacente, a hipotenusa é a mesma. Assim:
a = hipotenusa;
b = cateto adjacente ao ângulo ;
c = cateto oposto ao ângulo .
Agora que já sabemos nomear os lados do triângulo retângulo, devemos conhecer
as relações trigonométricas que podem ser aplicadas neste tipo de triângulo.
Dois triângulos retângulos semelhantes (mesmos ângulos internos, mas lados com
tamanhos diferentes) possuem o mesmo resultado para a razão (divisão) entre dois
de seus lados, conforme ilustrado a seguir:
1) '
'
b b
a a

, observe que aqui está sendo dividido o cateto oposto ao ângulo 
pela hipotenusa de cada triângulo. A essa razão dá-se o nome de seno, portanto:
cateto oposto
seno do ângulo
hipotenusa
 

10. 9
De maneira simplificada:
co
sen
hip
 
2) '
'
c c
a a

, observe que aqui está sendo dividido o cateto adjacente ao ângulo
 pela hipotenusa de cada triângulo. A essa razão dá-se o nome de cosseno,
portanto:
cos
cateto adjacente
seno do ângulo
hipotenusa
 
De maneira simplificada:
cos
ca
hip
 
2) '
'
b b
c c

, observe que aqui está sendo dividido o cateto oposto pelo cateto
adjacente ao ângulo  de cada triângulo. A essa razão dá-se o nome de tangente,
portanto:
tan
cateto oposto
gente do ângulo
cateto adjacente
 
De maneira simplificada:
co
tg
ca
 
Portanto, seno, cosseno e tangente de um ângulo nada mais é do que a divisão
entre dois lados de um triângulo retângulo. A tabela 2 indica alguns valores para
seno, cosseno e tangente, mas a calculadora científica pode fornecer valores para
qualquer ângulo através das teclas:
Figura 1: Teclas para utilizar as funções seno, cosseno e tangente na calculadora científica.

11. 10
Deve-se tomar o cuidado de verificar se a calculadora está adequada para calcular
em graus (D), radianos (R) ou gradianos (G). Isso é verificado na parte superior do
visor da calculadora.
Figura 2: Visor de uma calculadora científica. Observe que aparece a letra D na parte
superior do visor, indicando que a calculadora está programada para trabalhar em graus.
Ângulo seno cosseno tangente
0o
0 1 0
10o
0,174 0,985 0,176
20o
0,342 0,940 0,364
30o
0,500 0,866 0,577
40o
0,643 0,766 0,839
50o
0,766 0,643 1,192
60o
0,866 0,500 1,732
70o
0,940 0,342 2,747
80o
0,985 0,174 5,671
90o
1 0 Não existe
180o
0 -1 0
270o
-1 0 Não existe
360o
0 1 0
Tabela 2: Valores de seno, cosseno e tangente de alguns ângulos.
Exemplos:
1) Determine os valores de X nos triângulos retângulos a seguir:
a)
O primeiro passo é identificar o que foi fornecido no
triângulo:
Hipotenusa (hip) = 8 mm
Ângulo () = 20o
Cateto oposto (co) = X

12. 11
Das três relações trigonométricas a que devemos utilizar é a do seno, pois a do
cosseno e da tangente utiliza o cateto adjacente e ele não foi fornecido, assim:
20
8
o
co
sen
hip
X
sen
 

Multiplicando em “cruz”, temos:
8. 20
2,74
o
X sen
X mm


b)
A relação trigonométrica adequada é o cosseno, pois é a única que tem hipotenusa
e cateto adjacente, assim:
cos
12
cos 40o
ca
hip
X
 

.cos 40 12
12
cos 40
15,66
o
o
X
X
X cm



c)
Dados:
Hipotenusa (hip) = X
Ângulo () = 40o
Cateto adjacente (ca) = 12 cm
Dados:
Ângulo () = 31,9o
Cateto oposto (co) = 16 mm
Cateto adjacente (ca) = X

13. 12
A relação trigonométrica adequada é a tangente, pois é a única que possui cateto
oposto e cateto adjacente, assim:
16
31,9o
co
tg
ca
tg
X
 

Multiplicando em “cruz”, temos:
. 31,9 16
16
31,9
25,71
o
o
X tg
X
tg
X cm



2) Determine os ângulos  dos seguintes triângulos retângulos:
a)
A relação trigonométrica adequada é o seno, pois é a única que possui cateto
oposto e hipotenusa, assim:
10
15
0,667
co
sen
hip
sen
sen






Mas queremos calcular o ângulo  e não o seno do ângulo , assim, devemos
utilizar as teclas “shift” + “sin” da calculadora, pois a tecla “shift” (ou qualquer
outra tecla que ative a segunda função da calculadora) irá ativar o inverso do seno
que é a função “sin-1
”. Portanto:
1
(0,667)
41,84o
sen




Dados:
Hipotenusa (hip) = 15 mm
Cateto oposto (co) = 10 mm

14. 13
Apertando a tecla da calculadora indicada a seguir teremos o resultado em graus,
minutos e segundos:
41 50´24´´o
 
b)
A relação trigonométrica adequada é a tangente, pois é a única que possui cateto
oposto e cateto adjacente, assim:
1
82
74
82
74
47,94
47 56' 24''
o
o
co
tg
ca
sen
tg








 
  
 


c)
A relação trigonométrica adequada é o cosseno, pois é a única que possui cateto
adjacente e hipotenusa, assim:
Dados:
Cateto adjacente (ca) = 74 mm
Cateto oposto (co) = 82 mm
Dados:
Cateto adjacente (ca) = 10 mm
Hipotenusa (hip) = 32 mm

15. 14
1
cos
10
cos
32
10
cos
32
71,79
71 47' 24''
o
o
ca
hip








 
  
 


Relações trigonométricas num triângulo qualquer
As relações trigonométricas estudadas no capítulo anterior servem apenas para
triângulos retângulos. Quando um triângulo não é retângulo, existem outras
relações para calcular algum lado e/ou algum ângulo do triângulo. Essas relações
são conhecidas como lei dos senos e lei dos cossenos.
Lei dos senos
Observe o triângulo a seguir:
Se dividirmos um lado pelo seno do ângulo oposto, teremos os seguintes
resultados:
12
18,66
40
9,33
18,66
30
17,54
18,66
110
o
o
o
sen
sen
sen



Observe que os resultados são iguais, isto é, as medidas dos lados são
proporcionais aos senos dos ângulos opostos. Esta é a lei dos senos e ela pode ser
utilizada em qualquer triângulo, inclusive o retângulo.

16. 15
1 2
1 2
lado lado
seno do ângulo oposto ao lado seno do ângulo oposto ao lado

Ou
1 3
1 3
lado lado
seno do ângulo oposto ao lado seno do ângulo oposto ao lado

Ou
2 3
2 3
lado lado
seno do ângulo oposto ao lado seno do ângulo oposto ao lado

Exemplos:
1) Monte a expressão da lei dos senos para o triângulo a seguir:
a b c
sen sen sen  
 
2) Calcule o valor de x nos triângulos a seguir:
a)

17. 16
0 0
0 0
0
0
80
40 120
. 120 80. 40
80. 40
120
59,38
X
sen sen
X sen sen
sen
X
sen
X mm




b)
Como a soma dos ângulos internos de um triângulo deve ser igual a 1800
, então o
triângulo terá os seguintes ângulos:
3) Calcule os valores de X e Y no triângulo a seguir:
Aplicando a lei dos senos:
Aplicando a lei dos senos:

18. 17
4) Calcule o ângulo  nos triângulos a seguir:
a)
b)
Lei dos cossenos
A lei dos cossenos é menos empregada que a lei dos senos devido à simplicidade
da equação da lei dos senos, mas em algumas situações, a resolução através da lei
dos cossenos se torna a forma mais rápida.
A lei dos cossenos também pode ser aplicada em um triângulo qualquer, inclusive
o retângulo. Sua definição é a seguinte:
O quadrado da medida de um lado é igual à soma das medidas dos quadrados dos
outros dois lados (até aqui lembra o teorema de Pitágoras) menos duas vezes o
produto destes lados pelo cosseno do ângulo formado entre eles.

19. 18
Para simplificar a definição da lei dos cossenos, vamos utilizar como exemplo o
triângulo abaixo:
Traduzindo a definição, têm-se:
2 2 2
2. . .cosa b c b c   
Exemplos:
1) Calcule o valor de X no triângulo a seguir:
2) Calcule o valor de  no triângulo a seguir:
Observe que o triângulo tem todos os lados iguais, isto é, ele é equilátero. Assim, o
triângulo também terá todos os ângulos iguais e como a soma dos ângulos internos
Aplicando a lei dos cossenos:

20. 19
é igual a 1800
, então cada ângulo tem 600
, isto é o ângulo  vale 600
. Utilizando a
lei dos cossenos, vamos provar que seu valor é de 600
.
Neste caso, nós temos os três lados e queremos calcular o ângulo, assim:
2 2 2
1
0
30 30 30 2.30.30.cos
900 900 900 1800.cos
900 1800 1800.cos
900 1800 1800.cos
900
cos
1800
0,5 cos
cos (0,5)
60









  
  
 
  






Área dos principais polígonos
O cálculo de área é utilizado com muita frequência na Engenharia e, portanto, todo
engenheiro deve dominar esse assunto.
Área do retângulo: O retângulo é um quadrilátero (polígono de quatro lados) que
possui os quatro ângulos internos iguais a 900
. Sua área é definida como o produto
da medida da base (b) pela medida da altura (h).
Área do quadrado: O quadrado é um retângulo que possui o mesmo valor para a
base (b) e para a altura (h=b). Assim, sua área também é dada pelo produto da base
pela altura.

21. 20
Área do paralelogramo: O paralelogramo é um quadrilátero que não possui
ângulos internos de 90º, mas possui seus lados opostos paralelos. A sua área
também é calculada como o produto da base (b) pela altura (h).
Área do triângulo: É calculada pelo produto da base (b) pela altura (h) dividido
por dois, pois se dividirmos o quadrado, ou o retângulo, ou o paralelogramo ao
meio, teremos dois triângulos iguais, e por isso que a área do triângulo tem essa
divisão por dois.
Área do losango: O losango é um quadrilátero com os quatro lados iguais e não
paralelos. Sua área é definida como o produto de sua diagonal maior (D) pela
diagonal menor (d) dividido por dois.
Área do trapézio: O trapézio é um quadrilátero que possui dois lados paralelos e
dois lados não paralelos, sendo que os seus lados paralelos recebem os nomes de
base. Sua área é calculada pelo produto da altura (h) pela soma de suas bases (B+b)
divididos por dois.

22. 21
( ).
2
B b h
A


Perímetro dos polígonos
O perímetro de um polígono é definido como a soma de todos os seus lados
Exemplos:
1)
2)
Circunferência e círculo
Circunferência é uma figura geométrica representada por uma linha contida num
plano que possui uma mesma distância de um ponto que é denominado de centro
da circunferência. Círculo é toda região que compreende a circunferência, isto é,
circunferência é somente a linha externa enquanto círculo é região interna da
circunferência.
Circunferência Círculo

23. 22
A distância do centro da circunferência (0) até a linha periférica (externa) é
denominada de raio (R) e o dobro do raio é denominado diâmetro (d).
Comprimento da circunferência (perímetro)
Curvando uma linha podemos fazer uma circunferência de diâmetro d, sendo que o
comprimento dessa linha é chamado de perímetro ou comprimento da
circunferência (p). Existe uma relação muito interessante e importante entre o
comprimento da linha (perímetro) e o diâmetro da circunferência formada pela
linha: Se dividirmos qualquer comprimento de linha pelo diâmetro que ela forma,
teremos sempre o mesmo resultado, e esse resultado tem um valor muito
conhecido e utilizado na matemática, o número  (3,14159265...),
matematicamente:
.
2. , :
2
p
d
p d
Como d R então
p R







Exemplos:
1) Qual o perímetro de uma circunferência de raio 20 m?
2
2 20
40
125,66
p R
p
p
p m








24. 23
2) Qual o diâmetro que conseguimos formar com uma linha de 300 mm de
comprimento?
Resposta: O perímetro da circunferência é o comprimento da linha (300 mm),
então:
.
300 .
300
95,49
p d
d
d
p mm







3) Determine a distância em linha reta percorrida por uma roda de 250 mm de raio
quando ela realiza uma volta completa.
Resposta: A distância percorrida em uma volta é exatamente o perímetro da roda,
assim:
2
2 250
500
1570,8
p R
p
p
p mm







Área de um círculo
A área de um círculo é definida como o produto de  pelo quadrado da medida de
seu raio.
Exemplo: Calcule a área de um círculo de diâmetro igual a 20 mm.
Resposta: O raio vale 10 mm, pois ele é a metade do diâmetro, assim:
2
2
.
.10
100.
314,16
A R
A
A
A mm








25. 24
Radiano
Um radiano é o valor que ângulo central (adquirequando o comprimento do
arco da circunferência possui o mesmo valor do raio da circunferência.
Em uma metade de qualquer circunferência (1800
) é observado que o comprimento
do arco equivale a 3,14159... raios de circunferência, isto é:
1800
=  rad (relação entre graus e radianos).
Exemplo:
1) Converta para radianos as seguintes medidas de ângulos:
a) 300
0
0
180
30 x


Multiplicando em “cruz”:
180. 30.
30.
180
6
0,52
x
x
x rad
x rad







b) 450
Multiplicando em “cruz”:

26. 25
c) 600
0
0
180
60 x


180. 60.
60.
180
3
1,05
x
x
x rad
x rad







2) Converta as seguintes medidas de ângulos em graus:
a) 0,76 rad
0
180
0,76x


0
0
. 180.0,76
180.0,76
43,54
43 32'24''
x
x
x
x






Volume de alguns sólidos geométricos
Para finalizar essa introdução à Geometria, é necessário estudarmos o volume dos
sólidos que são muito utilizados em projetos de Engenharia, o paralelepípedo, o
cilindro e a esfera.
Paralelepípedo: São sólidos cujas bases são paralelogramos. Os paralelepípedos
que iremos estudar são os retos-retângulos e o cubo.
O paralelepípedo reto-retângulo possui todos os ângulos internos iguais a 900
.
Todos os cantos de qualquer paralelepípedo são chamados de arestas.
d) 2700
b) 4,73 rad

27. 26
aresta
O volume deste tipo de paralelepípedo é calculado multiplicando-se todos os seus
lados:
. .V a b c
O cubo é um paralelepípedo que possui todos os seus lados iguais e, também,
possui todos os ângulos internos iguais a 900
.
O seu volume também é calculado multiplicando-se todos os seus lados:
3
. .V a a a
V a


Cilindro: Muito parecido com os paralelepípedos, mas apresenta bases circulares.
O seu volume é calculado pelo produto (multiplicação) da área da base circular
(Ab) pela sua altura (h).

28. 27
.bV A h
Como a área de um círculo é dada por
2
.bA R , então:
2
. .V R h
Esfera: É um sólido que possui uma superfície externa que está a uma mesma
distância até o seu centro, sendo esta distância denominada raio da esfera.
O seu volume é calculado pela seguinte expressão:
3
4. .
3
R
V


A área da superfície esférica é calculada por:

29. 28
Referências Bibliográficas
GIOVANNI, J. R. & BONJORNO, J. R. Matemática: uma nova abordagem. FTD, São Paulo, 2000.
LIPSCHUTZ, S. Álgebra Linear. McGraw-Hill, USA, 1978.
OLIVEIRA, I. C. & BOULOS, P. Geometria Analítica: um tratamento vetorial. McGraw-Hill, São
Paulo, 1986.
REIS, I. Fundamentos da Matemática. Moderna. São Paulo, 1997.
SMOLE, K. C.S. & KIUKAWA, R. Matemática. Saraiva, São Paulo, 1998.