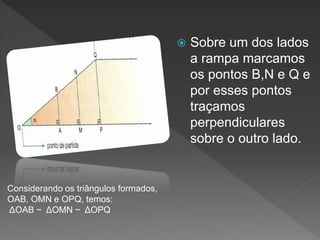
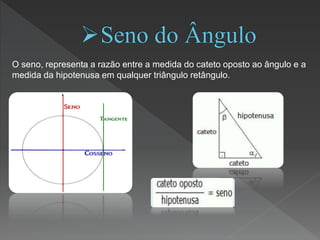
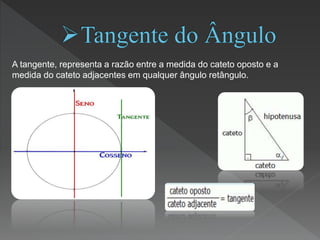
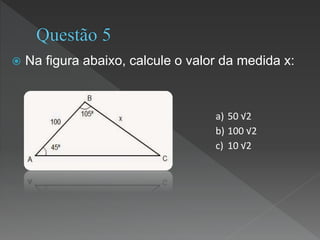
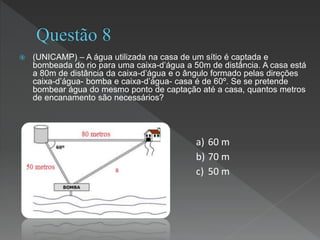
Este documento discute os conceitos fundamentais da trigonometria, incluindo as relações trigonométricas em triângulos retângulos e quaisquer, assim como a lei dos senos e cossenos. Aplica esses conceitos para resolver problemas envolvendo distâncias e ângulos.

2.  História da Trigonometria;
 Relações Trigonométricas de um Triângulo Retângulo;
 Seno, Cosseno e Tangente de um Triângulo Retângulo;
 Problemas no Triângulo Retângulo;
 Atividades;
 As Relações Trigonométricas em um Triângulo
Qualquer;
 Topografia;
 Lei dos Senos e Cossenos;
 Atividades;

3.  A palavra trigonometria significa
medida das partes de um triângulo.
Não se sabe ao certo se o conceito
da medida de ângulo surgiu com os
gregos ou se eles, por contato com a
civilização babilônica, adotaram suas
frações sexagesimais. Mas os
gregos fizeram um estudo
sistemático das relações entre
ângulos - ou arcos - numa
circunferência e os comprimentos de
suas cordas.

5.  Vamos supor que a figura
seguinte seja uma rampa
na qual destacamos o
ângulo de medida a (ou
simplesmente ângulo
alfa), chamado Ângulo
de Subida.

6.  Sobre um dos lados
a rampa marcamos
os pontos B,N e Q e
por esses pontos
traçamos
perpendiculares
sobre o outro lado.
Considerando os triângulos formados,
OAB, OMN e OPQ, temos:
ΔOAB ~ ΔOMN ~ ΔOPQ

7. O seno, representa a razão entre a medida do cateto oposto ao ângulo e a
medida da hipotenusa em qualquer triângulo retângulo.

8. O cosseno, representa a razão entre a medida do cateto adjacente
e a medida da hipotenusa em qualquer triângulo retângulo.

9. A tangente, representa a razão entre a medida do cateto oposto e a
medida do cateto adjacentes em qualquer ângulo retângulo.

10. O seno, o cosseno e a
tangente do ângulo, são
denominados razões
trigonométricas

11.  Usando os valores do seno, do cosseno e
da tangente de um ângulo agudo de um
triângulo retângulo, podemos resolver
problemas. Acompanhe as situações a
seguir:

12.  (Cefet – PR) A Rua Tenório Quadros e a Avenida Teófilo
Silva, ambas retilíneas, cruzam-se conforme um ângulo
de 30º. O posto de gasolina Estrela do Sul encontra-se na
Avenida Teófilo Silva a 4 000 m do citado cruzamento.
Portanto, determine em quilômetros, a distância entre o
posto de gasolina Estrela do Sul e a Rua Tenório
Quadros?
a) 2266 m
b) 6800 m
c) 5200 m

13.  (Unisinos – RS) Um avião levanta voo sob um ângulo
constante de 20º. Após percorrer 2 000 metros em linha
reta, qual será a altura atingida pelo avião,
aproximadamente? (Utilize: sem 20º = 0,342; cos 20º =
0,94 e tg 20º = 0,364).
a) 1880
b) 684
c) 728

14.  (UF – PI) Um avião decola, percorrendo uma
trajetória retilínea, formando com o solo, um
ângulo de 30º (suponha que a região
sobrevoada pelo avião seja plana). Depois
de percorrer 1 000 metros, qual a altura
atingida pelo avião?
a) 1700
b) 566,6...
c) 500

15.  De um ponto A, um agrimensor enxerga o topo
T de um morro, conforme um ângulo de 45º. Ao
se aproximar 50 metros do morro, ele passa a
ver o topo T conforme um ângulo de 60º.
Determine a altura do morro.
a) X= 121,38 / Y~= 71,4
b) X= 122,40 / Y~= 70,3
c) X= 120,52 / Y~= 60,5

16.  Algumas vezes deparamos com plantas de
terrenos em que há a representação de lagos
ou de montanhas com todas as medidas
indicadas sem que nos ocorra pensar em
como essas medidas teriam sido obtidas.
 A topografia é a área da Engenharia que trata
de situações como esta: medições que
determinam a forma e a posição de elementos
do relevo, com base em relações
estabelecidas pela Trigonometria. Para isso,
utiliza-se o teodolito, um instrumento de
observação que ajuda a calcular distâncias
difíceis de serem medidas, a partir de medidas
de triângulos que podem ser determinados nos
terrenos

17. O conhecimento das relações entre
lados e ângulos desses triângulos é
fundamental para o topógrafo, pois se
ele conhecer três das seis medidas
de lados e ângulos de um triângulo
poderá calcular as demais.
Até a descoberta dessas relações,
problemas que envolvessem triângulos
eram geralmente resolvidos com o que
se sabia das relações no triângulo
retângulo, mas a prática mostrou que isso era insuficiente ou tornava os
Cálculo muito trabalhosos.
A determinação das medidas dos ângulos e dos comprimentos dos lados de
um triângulo qualquer, sem recorrer aos triângulos retângulos, foi possível com
a evolução da Trigonometria. As relações, chamadas lei dos senos e
lei dos cossenos, trouxeram ferramentas fundamentais para os problemas que
envolviam esse triângulos.

18.  A lei dos senos estabelece a relação entra a
medida de um lado e o seno do ângulo oposto a
esse lado. Para um triângulo ABC de lados a, b, c,
podemos escrever.

19.  A lei dos cosseno em qualquer triângulo, o quadrado de um
lado é igual à soma dos quadrados dos outros dois, menos
duas vezes o produto desses dois lados pelo cosseno do
ângulo formado por eles.

20.  Na figura abaixo, calcule o valor da medida x:
a) 50 √2
b) 100 √2
c) 10 √2

21.  Calcule a medida do lado x. Dados: sen45°=
0,707; sen120°= 0,866.
a) 183,88 cm
b) 198,33 cm
c) 183,73 cm

22.  Os lados de um triângulo são 3, 4 e 6. Calcule o
cosseno do maior ângulo interno desse triângulo.
a) -11/24
b) -10/24
c) -1/24

23.  (UNICAMP) – A água utilizada na casa de um sítio é captada e
bombeada do rio para uma caixa-d’água a 50m de distância. A casa está
a 80m de distância da caixa-d’água e o ângulo formado pelas direções
caixa-d’água- bomba e caixa-d’água- casa é de 60º. Se se pretende
bombear água do mesmo ponto de captação até a casa, quantos metros
de encanamento são necessários?
a) 60 m
b) 70 m
c) 50 m

24. Isabele Félix N°8
Jamile Fontenele N°9
Jamille Miranda N°10
Beatriz Fontenele N°15