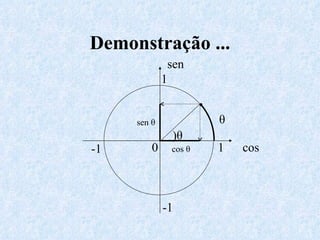
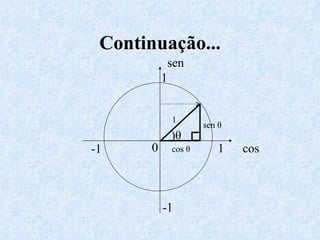
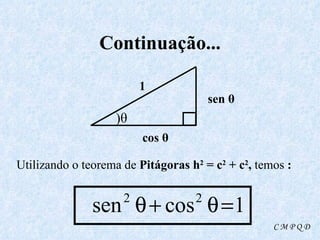
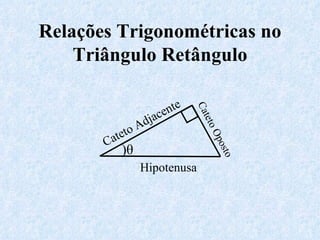
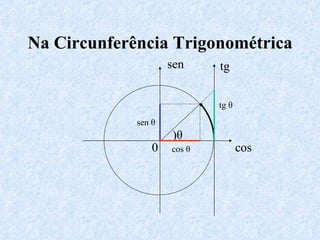
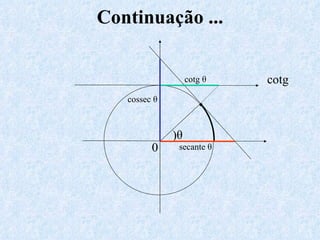
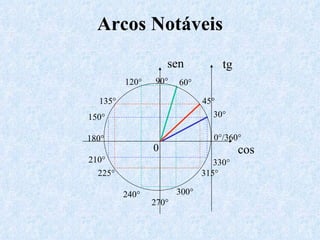
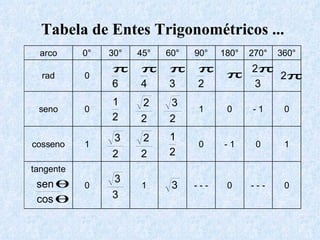
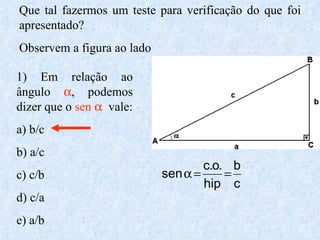
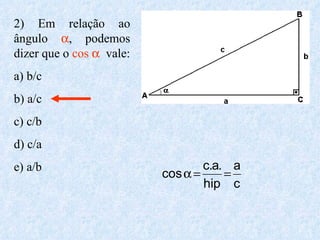
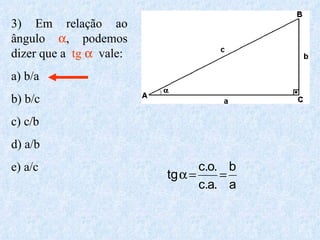
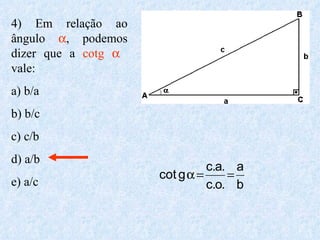
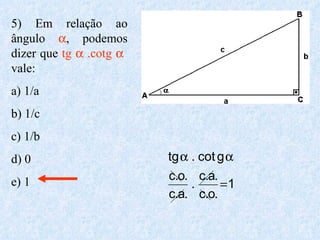
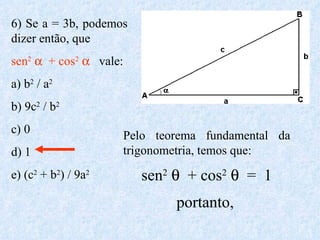
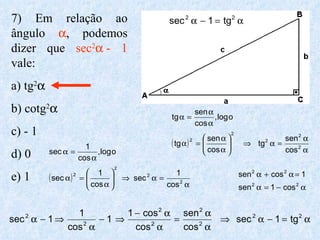
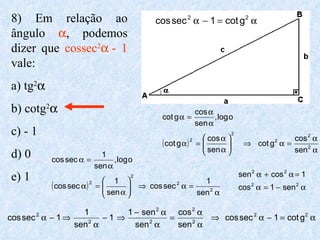
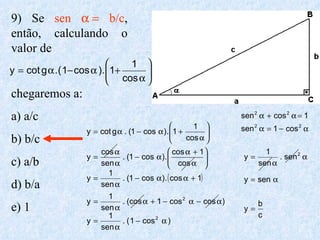
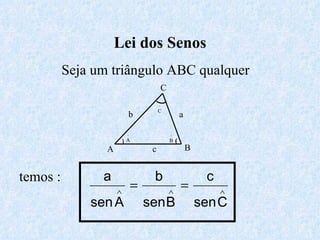
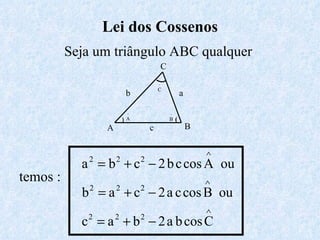
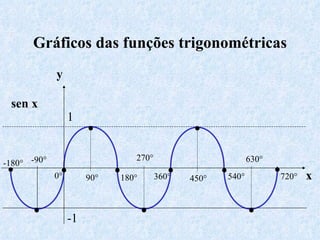
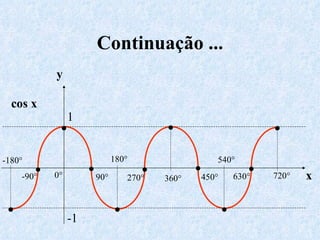
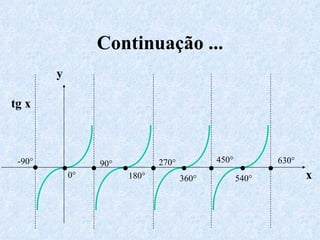
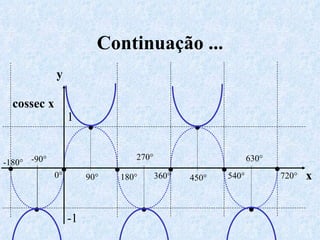
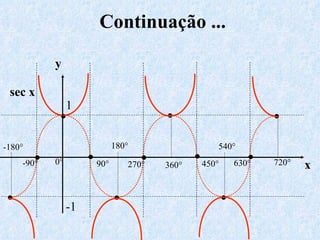
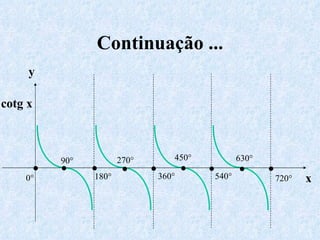
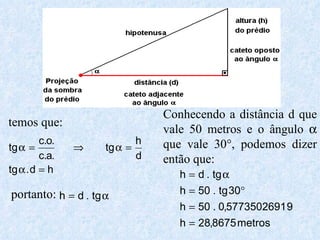
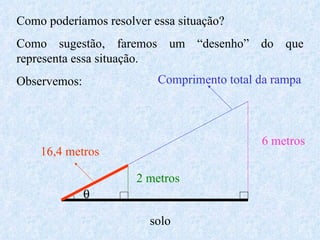
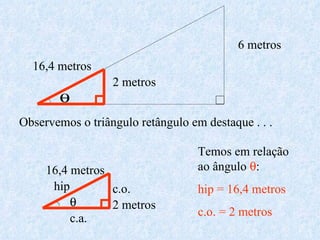
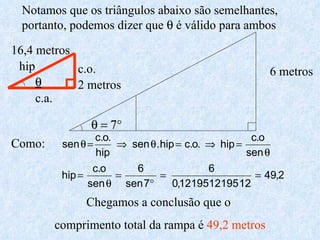
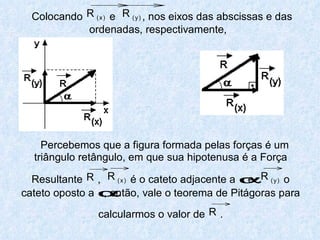
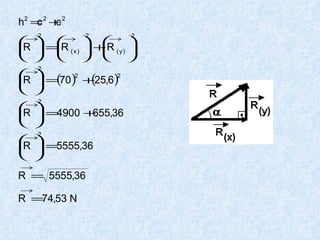
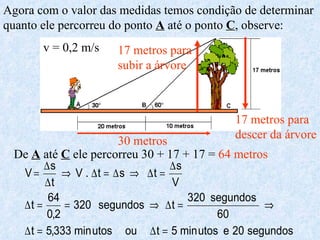
O documento apresenta os conceitos fundamentais da trigonometria, incluindo o teorema fundamental da trigonometria, relações trigonométricas, funções trigonométricas e suas aplicações em geometria e mecânica. Há também exemplos numéricos para exercitar os conceitos apresentados.

1. Teorema Fundamental da Trigonometria

2. Demonstração ... )θ θ · 1 cos sen 1 -1 -1 0 sen θ cos θ

3. Continuação... )θ 1 cos sen 1 -1 -1 0 sen θ cos θ 1

4. Continuação... Utilizando o teorema de Pitágoras h 2 = c 2 + c 2 , temos : C M P Q D )θ sen θ cos θ 1

5. Relações Trigonométricas no Triângulo Retângulo Cateto Adjacente Cateto Oposto Hipotenusa ) θ

6. Continuação ... Cotangente de θ Secante de θ Cossecante de θ Tangente de θ Cosseno de θ Seno de θ Relação no Triângulo Retângulo Ente Trigonométrico

7. Na Circunferência Trigonométrica )θ cos sen 0 · tg sen θ cos θ tg θ

8. Continuação ... )θ 0 · cotg cotg θ secante θ cossec θ

9. Arcos Notáveis 30° 45° 60° 150° 210° 330° 135° 225° 315° 120° 240° 300° cos sen 0 tg 90° 180° 270° 0°/360°

10. Tabela de Entes Trigonométricos ...

11. Vamos pensar . . .

12. Que tal fazermos um teste para verificação do que foi apresentado? Observem a figura ao lado 1) Em relação ao ângulo  , podemos dizer que o sen  vale: a) b/c b) a/c c) c/b d) c/a e) a/b

13. 2) Em relação ao ângulo  , podemos dizer que o cos  vale: a) b/c b) a/c c) c/b d) c/a e) a/b

14. 3) Em relação ao ângulo  , podemos dizer que a tg  vale: a) b/a b) b/c c) c/b d) a/b e) a/c

15. 4) Em relação ao ângulo  , podemos dizer que a cotg  vale: a) b/a b) b/c c) c/b d) a/b e) a/c

16. 5) Em relação ao ângulo  , podemos dizer que tg  .cotg  vale: a) 1/a b) 1/c c) 1/b d) 0 e) 1

17. 6) Se a = 3b, podemos dizer então, que sen 2  + cos 2  vale: a) b 2 / a 2 b) 9c 2 / b 2 c) 0 d) 1 e) (c 2 + b 2 ) / 9a 2 Pelo teorema fundamental da trigonometria, temos que: sen 2  + cos 2  = 1 portanto,

18. 7) Em relação ao ângulo  , podemos dizer que sec 2  - 1 vale: a) tg 2  b) cotg 2  c) - 1 d) 0 e) 1

19. 8) Em relação ao ângulo  , podemos dizer que cossec 2  - 1 vale: a) tg 2  b) cotg 2  c) - 1 d) 0 e) 1

20. 9) Se sen  b/c , então, calculando o valor de chegaremos a: a) a/c b) b/c c) a/b d) b/a e) 1

21. Voltando a parte teórica

22. Lei dos Senos Seja um triângulo ABC qualquer temos : ) ( A B C a c b

23. Lei dos Cossenos Seja um triângulo ABC qualquer temos : ) ( A B C a c b

24. Continuação ... Curiosidade : Quando um dos ângulos do triângulo é reto, por exemplo, Â= 90°, temos : Sabe-se que cos 90° = 0, logo ... Temos, portanto ... Teorema de Pitágoras

25. Gráficos das funções trigonométricas sen x y x • • • • • • • • • • 0° 540° 720° 450° 630° 360° 270° 180° -180° -90° • 90° 1 -1

26. Continuação ... cos x y x • • • • • • • • • • • 0° 540° 720° 450° 630° 360° 270° 180° -180° -90° 90° 1 -1

27. Continuação ... tg x y x • • • • • • • • • 0° 360° -90° 90° 180° 270° 450° 540° 630°

28. Continuação ... • • • • • • • • • • y x 0° 540° 720° 450° 630° 360° 270° 180° -180° -90° • 90° 1 -1 cossec x

29. Continuação ... • • • • • • • • • • • 0° 540° 720° 450° 630° 360° 270° 180° -180° -90° 90° sec x y x 1 -1

30. Continuação ... cotg x y x • • • • • • • • • 0° 360° 90° 180° 270° 450° 540° 630° 720°

31. TRIGONOMETRIA APLICADA • Modelo matemático que indica ao número de horas do dia, com luz solar, de uma determinada cidade norte americana, “ t” dias após 1º de janeiro. Fonte : J.Stewart – Cálculo vol. I – Pág. 34

32. Continuação ... Fonte : J.Stewart – Cálculo vol. I – Pág. 394 • Função de Fresnel , assim chamada em homenagem ao físico francês Augustin Fresnel (1788-1827), famoso por seus trabalhos em ótica. Esta função foi primeiramente apresentada num trabalho sobre difração de ondas de luz de Fresnel, porém recentemente foi aplicado no planejamento de auto-estradas.

33. Continuação ... • Integração por Substituição trigonométrica Demonstrando o Caso I ... C M P Q D

34. Trigonometria Algumas Aplicações

35. Parte Prática O exemplo clássico da Sombra Para que possamos medir (aproximadamente) a altura de um prédio, sem a necessidade de subir ao terraço, ou utilizar equipamentos sofisticados, seria necessário somente 2 elementos. São eles: uma distância um ângulo Observe a seguir . . .

36. temos que: portanto: Conhecendo a distância d que vale 50 metros e o ângulo  que vale 30°, podemos dizer então que:

37. Exemplo 1 A inclinação de uma rampa

38. Uma rampa com inclinação constante, (como a que existe em Brasília) tem 6 metros de altura na sua parte mais elevada. Um engenheiro começou a subir, e nota que após ter caminhado 16,4 metros sobre a rampa está a 2,0 metros de altura em relação ao solo. Será que este engenheiro somente com esses dados e uma calculadora científica conseguiria determinar o comprimento total dessa rampa e sua inclinação em relação ao solo?

39. Como poderíamos resolver essa situação? Como sugestão, faremos um “desenho” do que representa essa situação. Observemos: 6 metros 16,4 metros 2 metros  Comprimento total da rampa solo

40. Observemos o triângulo retângulo em destaque . . .  2 metros 16,4 metros hip c.o. c.a. Temos em relação ao ângulo   hip = 16,4 metros c.o. = 2 metros

41.  2 metros 16,4 metros hip c.o. c.a. Como: hip = 16,4 metros c.o. = 2 metros Obs.: quando dizemos que arcsen  = 1/2 , podemos transformar essa igualdade em uma pergunta: “qual é o arco, cujo seno vale 1/2?”, a resposta seria dizer que  = 30°.

42. Em nosso exercício, chegamos a conclusão que: sen  = 0,121951219512, logo podemos encontrar o ângulo  , com o auxílio da calculadora que normalmente utiliza as funções ASIN ou SIN -1 , então, devemos digitar 0,121951219512 e a opção acima de sua calculadora. Se o processo foi realizado corretamente, deverá ser encontrado o valor 7,00472640907 , que iremos considerar como aproximadamente 7° . Encontramos assim, a inclinação da rampa!

43. 6 metros   2 metros 16,4 metros hip c.o. c.a. Notamos que os triângulos abaixo são semelhantes, portanto, podemos dizer que  é válido para ambos Como: Chegamos a conclusão que o comprimento total da rampa é 49,2 metros

44. Exemplo 2 Mecânica Geral ou Trigonometria?

45. Os conceitos trigonométricos aparecem com muita freqüência no estudo da Física, Topografia, Astronomia e de muitos outros assuntos. Observemos os exemplos a seguir: Em relação ao sistema de forças representado na figura, onde F 1 = 20N, F 2 = 100N, F 3 = 40N e F 4 = 10N, você seria capaz de determinar a intensidade da resultante do sistema e o ângulo que essa resultante forma com o eixo das abscissas (x)?

52. Desafio !

53. Um alpinista muito ágil, percorre um trajeto passando pelos pontos A e B . Não se sabe ao certo o que ocorreu, mas ele conseguiu com o material apropriado chegar a conclusão das medidas abaixo mencionadas. Quando chega até a árvore ele percebe que o único caminho que o levará até o ponto C é escalando-a. (a altura da árvore é representada por h - despreze a largura do tronco) Se sua velocidade média é de 0,2 m/s, quantos minutos ele demorou para sair do ponto A e chegar ao ponto C ? ( )

54. Solução: Resumidamente, temos o triângulo ao lado que representa nosso desafio.

55. Igualando o h das equações ( I ) e (II) Como

56. 30 metros 17 metros para subir a árvore 17 metros para descer da árvore Agora com o valor das medidas temos condição de determinar quanto ele percorreu do ponto A até o ponto C , observe: De A até C ele percorreu 30 + 17 + 17 = 64 metros v = 0,2 m/s

57. Obrigado pela participação de todos!!! Infelizmente, terminou . . . Prof. Edson Arnaldo Mendes Prof. Paulo Alves Rodrigues