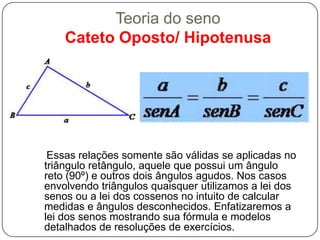
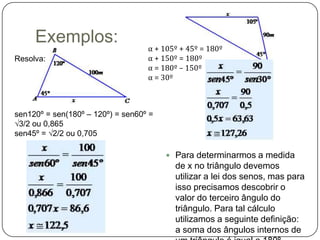
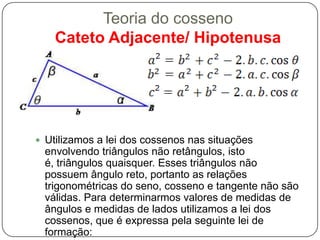
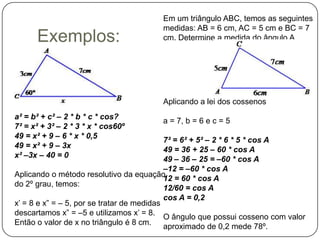
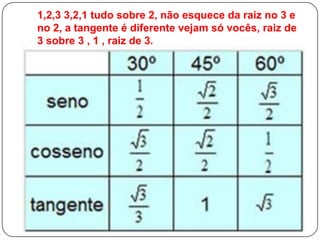
O documento explica as relações trigonométricas de seno, cosseno e tangente em triângulos retângulos, relacionando os ângulos com os lados opostos e adjacentes à hipotenusa. Também apresenta a lei dos senos para calcular medidas desconhecidas em triângulos quaisquer, e a lei dos cossenos para triângulos não retângulos.

1. Teoria de seno e
cosseno.
Os estudos trigonométricos no triângulo
retângulo têm por finalidade relacionar os
ângulos do triângulo com as medidas dos
lados, por meio das seguintes relações: seno,
cosseno e tangente. Essas relações utilizam o
cateto oposto, o cateto adjacente e a
hipotenusa.

2. Teoria do seno
Cateto Oposto/ Hipotenusa
Essas relações somente são válidas se aplicadas no
triângulo retângulo, aquele que possui um ângulo
reto (90º) e outros dois ângulos agudos. Nos casos
envolvendo triângulos quaisquer utilizamos a lei dos
senos ou a lei dos cossenos no intuito de calcular
medidas e ângulos desconhecidos. Enfatizaremos a
lei dos senos mostrando sua fórmula e modelos
detalhados de resoluções de exercícios.

3. Exemplos:
α + 105º + 45º = 180º
Resolva: α + 150º = 180º
α = 180º – 150º
α = 30º
sen120º = sen(180º – 120º) = sen60º =
√3/2 ou 0,865
sen45º = √2/2 ou 0,705
 Para determinarmos a medida
de x no triângulo devemos
utilizar a lei dos senos, mas para
isso precisamos descobrir o
valor do terceiro ângulo do
triângulo. Para tal cálculo
utilizamos a seguinte definição:
a soma dos ângulos internos de

4. Teoria do cosseno
Cateto Adjacente/ Hipotenusa
 Utilizamos a lei dos cossenos nas situações
envolvendo triângulos não retângulos, isto
é, triângulos quaisquer. Esses triângulos não
possuem ângulo reto, portanto as relações
trigonométricas do seno, cosseno e tangente não são
válidas. Para determinarmos valores de medidas de
ângulos e medidas de lados utilizamos a lei dos
cossenos, que é expressa pela seguinte lei de
formação:

5. Em um triângulo ABC, temos as seguintes
medidas: AB = 6 cm, AC = 5 cm e BC = 7
Exemplos: cm. Determine a medida do ângulo A.
Aplicando a lei dos cossenos
a² = b² + c² – 2 * b * c * cos?
a = 7, b = 6 e c = 5
7² = x² + 3² – 2 * 3 * x * cos60º
49 = x² + 9 – 6 * x * 0,5
7² = 6² + 5² – 2 * 6 * 5 * cos A
49 = x² + 9 – 3x
49 = 36 + 25 – 60 * cos A
x² –3x – 40 = 0
49 – 36 – 25 = –60 * cos A
–12 = –60 * cos A
Aplicando o método resolutivo da equação
12 = 60 * cos A
do 2º grau, temos:
12/60 = cos A
cos A = 0,2
x’ = 8 e x” = – 5, por se tratar de medidas
descartamos x” = –5 e utilizamos x’ = 8.
O ângulo que possui cosseno com valor
Então o valor de x no triângulo é 8 cm.
aproximado de 0,2 mede 78º.

6. 1,2,3 3,2,1 tudo sobre 2, não esquece da raiz no 3 e
no 2, a tangente é diferente vejam só vocês, raiz de
3 sobre 3 , 1 , raiz de 3.