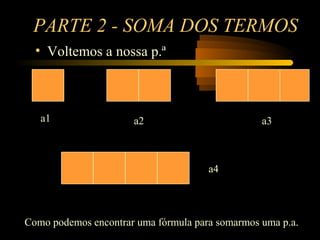
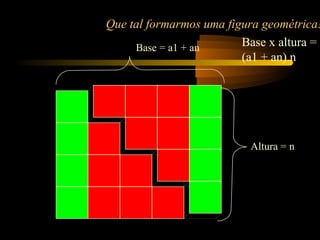
Este documento apresenta os conceitos básicos de progressão aritmética (P.A), incluindo a fórmula para o termo geral an = a1 + (n-1)r e a fórmula para a soma dos termos Sn = (a1 + an)n/2. Exemplos comuns de exercícios sobre P.A são apresentados e resolvidos para demonstrar a aplicação prática destas fórmulas.

1. UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
INSTITUTO DE MATEMÁTICA
LABORATÓRIO DE ENSINO - 2
Desenvolvido por:
Cristiano De Angelis

2. 1 - INTRODUÇÃO
• É comum, no nosso dia-a-dia, nos depararmos com situações nas
quais precisamos rever o passado, trabalhar com o presente e prever o
futuro.
• No caso da Matemática, que é o nosso instrumento de trabalho neste
momento, fazemos estas atividades por meio de cálculos.
• Quem nunca calculou o quanto pagará em uma prestação?
• E se ocorrerem aumentos progressivos?
• Vejamos um exemplo:

3. 1) Pagamos uma prestação de R$ 500,00
mensais. Se a prestação aumenta 50 reais a
cada mês, qual será o seu valor ao final de 2
anos?
2) E se quiséssemos calcular o quanto
pagamos no total, somando todos os meses?

4. • Estas duas perguntas, com certeza, tem uma
solução viável até por meios práticos. Mas
se a prestação fosse 501,23 e o aumento
mensal 51,88? Iríamos fazer da mesma
forma? Poderíamos ficar uma tarde
somando e, ao final, existiria grande
chances de ocorreu algum errinho.

5. • Questões como estas são comuns na nossa vida. E
as provas, sobretudo os vestibulares, exploram
estas questões, porém, de forma mais sofisticada.
• Vejamos os casos:

6. • Em todas as questões, temos uma situação inicial:
ACRESCENTANDO ALGUMA COISA, TEREMOS:
ACRESCENTANDO NOVAMENTE ESSA MESMA COISA, TEREMOS:
ACRESCENTANDO NOVAMENTE ESSA MESMA COISA, TEREMOS:
E ASSIM SUCESSIVAMENTE.

7. •
Mas e daí?

8. • Parece engraçado, mas este simples joginho
provoca verdadeiros estragos.
• Vejamos alguns:

9. • A nossa situação inicial ( ), chamamos de
“primeira situação”, ou “situação 1”, ou “termo
inicial”, ou , etc.
• A fim de padronizar este nome, que tal
chamarmos de a1!!!!
• Ora, se a primeira é a1, qual será a segunda?
Muito Bem, a2.
• E assim por diante, a3, a4, a5, etc..., até o último.
Como chamaremos o último termo?
• “A último”, ou “an”.

10. • Vamos, agora, estabelecer relações:
a1
a2 = a1 + 1 ACRÉSCIMO
a3 = a1 + 2 ACRÉSCIMOS

11. • Então:
• a2 = a1 + 1 acréscimo
• a3 = a1 + 2 acréscimos
• a4 = a1 + 3 Acréscimos
• a10 = a1 + 9 acréscimos
• a100 = a1 + 99 acréscimos
• ...
• an = a1 + (n-1) acréscimos

12. • Vamos chamar acréscimos de RAZÃO
ACRESCIDA, ou simplesmente razão.
• Abreviamos razão pela letra R.

13. Chegamos, então até a primeira fórmula importante desta aula
• an = a1 + (n-1).r
• de onde concluímos, também
• an = a2 + (n-2).r
• an = a3 + (n-3).r
• ...
• Chamaremos esta situação de Progressão Aritmética, ou
simplesmente P. A, onde :
• an = último termo da P.A
• a1 = primeiro termo da P.A
• n = nº de termos da P.A , indicado também pelo an.

14. • Uma outra consideração importante sobre p.a, ainda ~e
que, em qualquer p.ª, é que , um número menos o seu
antecessor, é igual ao antecessor menos o antecessor
seguinte, e assim por diante, ou seja,
• a6 - a5 = a5 - a4 = a4 - a3 = ... = r

15. • Como resolver os exercícios!!!!
• a) São dados duas variáveis de uma p.ª e é pedida a outra, diretamente com a
fórmula conhecida.
• A1 - em uma p.ª sabemos que o primeiro termo é = 5 e a razão = 2. Calcule o 10º
termo.
• A2 - em uma p.ª sabemos que o 30º termo = 62 e a razão = 2, calcule o 1º termo.
• A3 - em uma p.ª o primeiro termo = 2 e o 20º termo = 42. Qual o valor da razão:
• b) São dados também duas variáveis, mas pedido outro termo. Nesse caso
diviremos o exemplo em duas partes . Primeiro encontramos o a 1 e a razão. A
seguir, encontraremos o termo, ou os termos pedidos, ou então, usando a outra
versão da nossa fórmula, encontraremos diretamente o temo solicitado!!
• B1 - em um p.ª o quinto termo = 10 e a razão = 2. Encontre o oitavo termo.
• B2 - em uma p.ª o vigésimo termo é 60 e o décimo é 40. Encontre o primeiro termo.

16. • C) São dados a soma, subtração, divisão ou produto de dois termos
(geralmente a soma) e nos é solicitado algum termo ou a razão da p.ª
• c1) (unb-95) Em uma p.a, a soma do primeiro com o décimo termo é
igual a 28 e a soma do quinto com o oitavo termo é igual a 22. Qual a
razão desta p.a
• d) Existe, também, muitas outras maneiras de exercícios. Por exemplo
• d1) Inserindo 3 termos em uma p.ª ...
• D2) sabendo que a-1, a+5, a+11 formam uma p.ª, calcule o valor de a.

17. PARTE 2 - SOMA DOS TERMOS
• Voltemos a nossa p.ª
a1 a2 a3
a4
Como podemos encontrar uma fórmula para somarmos uma p.a.

18. Que tal formarmos uma figura geométrica!
Base = a1 + an Base x altura =
(a1 + an).n
Altura = n

19. Como a nossa p.a é a
metade da figura, então
também dividimos por dois, e chegamos a
Sn = (a1 + an) . n
2

20. • Com estas duas fórmulas (do termo geral e da
soma), mas os nosso conceitos básicos,
resolvemos qualquer exercício sobre p.ª
• Vejamos alguns exemplos de vestibular:

21. • (unicamp-sp) A soma dos dois primeiros termos
de uma p.ª é igual a 13 e dos cinco primeiros é
igual a 55. Determine o 31º termo
• a) 95 b) 245 c) 105 d) 235 e) 253
• (Fuvest-sp) Em uma progressão aritmética de
termos positivos, os 3 primeiros são 1 - a, -a,
raiz 11-1. O quarto termo é:
• a) 2 b) 3 c) 4 d) 5 e) 6

22. • (Fuvest-sp) A soma do 4º com o 8º termo de
uma P.ª é 20. O 31º é o dobro do 16º. A P.ª
é:
• a) -5, -2, 1
• b) 5, 6, 7
• c) 0, 2, 4
• d) 0, 3, 6
• e) 1, 3, 5

23. • (Fuvest-sp) Um automóvel percorre no
primeiro dia de viagem uma distancia x. No
segundo, o dobro do primeiro no terceiro o
triplo do primeiro, e assim sucessivamente.
• Ao final de 20 dias percorreu uma distancia
de 6.300 km. A distancia do primeiro dia foi
de:
• a) 15 b) 30 c) 20 d) 25 e) 35

24. CONCLUSÃO
• “Não é possível errarmos ou permitir que
nossos alunos errem qualquer questão sobre
p.a “
• Ricardo da Silva Gelak