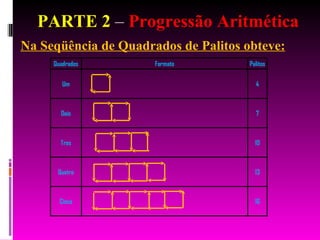
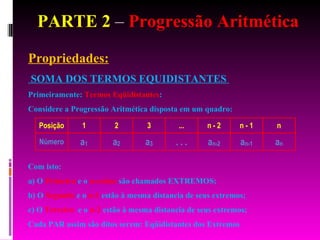
O documento explica o conceito de progressão aritmética, onde cada termo é igual ao anterior somado de um valor constante. Apresenta a definição formal, propriedades como o termo geral e a soma dos termos, e exemplos para verificar se sequências numéricas formam ou não progressões aritméticas. Finaliza com exercícios resolvidos sobre cálculo de termos, soma dos primeiros termos e inserção de termos intermediários em uma progressão dada.

1. Progressões Numéricas PARTE 2 – Progressão Aritmética

2. PARTE 2 – Progressão Aritmética Na Seqüência de Quadrados de Palitos obteve:

3. PARTE 2 – Progressão Aritmética A quantidade de Palitos Forneceu a Seqüência: 4 - 7 - 10 - 13 - 16 Pelo qual possui o detalhe: a) Q2 – Q1 = 7 – 4 = 3; b) Q3 – Q2 = 10 – 7 = 3 c) Q4 – Q3 = 13 – 10 = 3 d) Q5 – Q4 = 16 – 13 = 3 Isto está dizendo que um número da seqüência subtraído do anterior fornece sempre o mesmo valor ( aqui: 3 ); ao qual é o mesmo que dizer que um número é o anterior somado de um mesmo valor. Seqüência neste estilo é Chamado: Progressão Aritmética .

4. PARTE 2 – Progressão Aritmética Definição: Seja a seqüência numérica: : a 1 . a 2 . a 3 . a 4 . . . . .a n Esta seqüência diz ser uma Progressão Aritmética se ocorrer: a k = a k - 1 + r , em que r um número fixo. Ou seja : Cada Número é o anterior somado do mesmo valor.

5. PARTE 2 – Progressão Aritmética Nota: Na notação: : a 1 . a 2 . a 3 . a 4 . . . . .a n E: a k = a k - 1 + r Tem que: a 1 é o Primeiro Termo da Progressão Aritmética a n é o Termo Geral da Progressão Aritmética r é a Razão da Progressão Aritmética

6. PARTE 2 – Progressão Aritmética Exemplo 1: Para cada seqüência abaixo, verifique se é ou não uma Progressão Aritmética: : 11 . 15 . 19 . 23 . 27 . 31 . 35 Solução a 2 – a 1 = 15 – 11 = 4; a 3 – a 2 = 19 – 15 = 4; a 4 – a 3 = 23 – 19 = 4; a 5 – a 4 = 27 – 23 = 4; a 6 – a 5 = 31 – 27 = 4; a 7 – a 6 = 35 – 31 = 4; Ou Seja: A Diferença foi um mesmo valor, Assim trata-se de uma Progressão Aritmética .

7. PARTE 2 – Progressão Aritmética Exemplo 2: : 2,0 . 4,5 . 7,0 . 9,5 . 12,0 Solução a 2 – a 1 = 4,5 – 2,0 = 2,5; a 3 – a 2 = 7,0 – 4,5 = 2,5; a 4 – a 3 = 9,5 – 7,0 = 2,5; a 5 – a 4 = 12 – 9,5 = 2,5; Assim trata-se de uma Progressão Aritmética .

8. PARTE 2 – Progressão Aritmética Exemplo 3: : 5 . 11 . 17 . 22 . 28 Solução a 2 – a 1 = 11 – 5 = 6; a 3 – a 2 = 17 – 11 = 6; a 4 – a 3 = 22 – 17 = 5 ; a 5 – a 4 = 28 – 22 = 6; Como houve uma diferença com resultado diferente das demais, indica que NÃO configura uma Progressão Aritmética .

9. PARTE 2 – Progressão Aritmética Exemplo 4: Considere a seguinte construção geométrica: Encontrar a quantidade de Pontos na Interseção de Retas Co-planares e que não se interceptam mais de duas e não tenham nenhuma paralela a outra. Solução

10. PARTE 2 – Progressão Aritmética Exemplo 4 : Continuação

11. PARTE 2 – Progressão Aritmética Exemplo 4 : Continuação A seqüência de Pontos Foi : 1 . 3 . 6 . 10 Solução a2 – a1 = 3 – 1 = 2; a3 – a2 = 6 – 3 = 3; a4 – a3 = 10 – 6 = 4; Como houve diferenças com resultados diferentes dos outros , indica que NÃO configura uma Progressão Aritmética .

12. PARTE 2 – Progressão Aritmética Propriedades: TERMO GERAL Quando se tem uma Progressão Aritmética, seus valores satisfaz: 1. a 2 = a 1 + r = a 1 + (2 – 1 )r; 2. a 3 = a 2 + r = a 1 + r + r = a 1 + 2r = a 1 + (3 – 1)r 3. a 4 = a 3 + r = a 1 + 2r + r = a 1 + 3r = a 1 + (4 – 1)r 4. a 5 = a 4 + r = a 1 + 3r + r = a 1 + 4r = a 1 + (5 – 1)r De Forma Geral a n = a 1 + (n – 1)r

13. PARTE 2 – Progressão Aritmética Propriedades: SOMA DOS TERMOS EQUIDISTANTES Primeiramente: Termos Eqüidistantes : Considere a Progressão Aritmética disposta em um quadro: Com isto: a) O Primeiro e o n-ezimo são chamados EXTREMOS; b) O Segundo e o n-1 estão à mesma distancia de seus extremos; c) O Terceiro e o n-2 estão à mesma distancia de seus extremos; Cada PAR assim são ditos serem: Eqüidistantes dos Extremos

14. PARTE 2 – Progressão Aritmética Propriedades: SOMA DOS TERMOS EQUIDISTANTES Vamos calcular cada uma das somas abaixo: a) Primeiro com o último termo: S 1 = a 1 + a n b) Segundo com o penúltimo termo: S 2 = a 2 + a n-1 = a 1 + r + a n – r = a 1 + a n = S 1 c) Terceiro com o anti-penúltimo termo: S 3 = a 3 + a n-2 = a 1 + 2r + a n – 2r = a 1 + a n = S 1 Etc. Note que cada uma das somas de termos eqüidistantes dos extremos fornece sempre o mesmo resultado que é: O Valor do Primeiro Com do Último Termo.

15. PARTE 2 – Progressão Aritmética Propriedades: SOMA DOS TERMOS DA PROGRESSÃO A soma é: S = a 1 + a 2 + a 3 + a 4 + . . . . + a n Duplicando esta Soma fica: 2.S = a 1 + a 2 + a 3 + a 4 + . . . . + a n + + a 1 + a 2 + a 3 + a 4 + . . . . + a n Agrupando pelos termos eqüidistantes: 2.S = ( a 1 + a n ) + ( a 2 + a n-1 ) + . . . . Pela Propriedade da Soma dos Extremos tem-se: 2S = ( a 1 + a n ) + ( a 1 + a n ) + ( a 1 + a n ) + . . . Ou 2.S = n . ( a 1 + a n ) logo: S = ( a 1 + a n ) / 2

16. PARTE 2 – Progressão Aritmética Propriedades : Resumo

17. PARTE 2 – Progressão Aritmética Exercício 1 : Dada a Progressão Aritmética: :7 . 11 . 15 . 19 . . . ., Ache o que se pede: a) Valor do nono termo. Solução Primeiramente tem que achar a razão que é: r = 11 – 7 = 4 Com isto tem: Primeiro Termo: a 1 = 7 Aqui: n = 9. Logo: a 9 = 7 + ( 7 – 1 ) . 4 = 7 + 6 . 4 = 7 + 24 = 31. Resposta: O Nono termo é 31 .

18. PARTE 2 – Progressão Aritmética Exercício 1 : b) Valor do vigésimo termo. Solução A razão que é: r = 11 – 7 = 4 Primeiro Termo: a 1 = 7 Aqui: n = 20. Logo: a 9 = 7 + ( 20 – 1 ) . 4 = 7 + 19 . 4 = 7 + 56 = 63. Resposta: O Vigésimo termo é 63 .

19. PARTE 2 – Progressão Aritmética Exercício 1 : b) Valor da soma dos 20 primeiros termos. Solução A razão que é: r = 11 – 7 = 4 Primeiro Termo: a 1 = 7 Aqui: n = 20. Vigésimo Termo: 63 ( já calculado em b ) Logo: S20 = ( 7 + 63) . 20 / 2 = 70 . 20 / 2 = 700. Resposta: A soma é700 .

20. PARTE 2 – Progressão Aritmética Exercício 1 : b) Valor da soma dos 40 primeiros termos. Solução A razão que é: r = 11 – 7 = 4 Primeiro Termo: a 1 = 7 Aqui: n = 40. Vigésimo Termo: a 40 = 7 + (40 – 1 ) . 4 = 7 + 39 . 4 = 7 + 156 = 163 Logo: S 40 = ( 7 + 163) . 40 / 2 = 170 . 20 / 2 = 1 700. Resposta: A soma é: 1 700 .

21. PARTE 2 – Progressão Aritmética Exercício 3 : Inserir 7 meios entre: 2 e 42. Solução Nota: Inserir 7 Meios indica encontrar 7 números ao qual possua a mesma variação a partir do primeiro valor até o último fornecido: É equivalente a: Construir uma Progressão Aritmética em que os extremos são : 2 e 42 Com isto tem: Primeiro Termo: 2 ; Quantia de Termos: 9 ( 7 + 2 ) Nono Termo: 42 : Razão: Desconhecida Na forma geral: 42 = 2 + ( 9 – 1 ) . r assim: 42 – 2 = 8.r Ou: 8.r = 40 daí r = 40 / 8 = 5. Logo, a Progressão é: : 2 . 7 . 12 . 17 . 22 . 27 . 32 . 37 . 42. Os Meios inseridos são: : 7 , 12 , 17 , 22 , 27 , 32 e 37.

22. PARTE 2 – Progressão Aritmética Exercício 4 : Ache o total de palitos que foi usado na confecção de todos os quadrados do Exemplo Inicial desta Parte. Solução Para a sua construção usou, respectivamente: 4 – 7 – 10 – 13 e 16 palitos Com isto tem: Primeiro Termo: 4 ; Quantia de Termos: 5 Ultimo Termo: 16 : Razão: r = 7 – 4 = 3 Na forma da soma: S = ( 4 + 16) . 5 / 2 = 20 . 5 / 2 = 100/ 2 = 50 Resposta: 50 palitos.

23. Progressões Numéricas PARTE 2 - Progressão Aritmética FIM Prof. Gercino Monteiro Filho