Baixado 126 vezes
![2.2 TIPOS DE MATRIZES
[ ]
=
=
01
4
3
:EXEMPLO
AtipoDo-
coluna.únicaumaPossui-
:COLUNAMATRIZB)
543
:EXEMPLO
AtipoDo-
linha.únicaumaPossui-
:LINHAMATRIZA)
mx1
1xn
A
A
[ ]
=
==
=
=
497
6815
1410
62
83
;3
:EXEMPLO
n.mPortanto
colunas.denúmeroaoigualélinhasdenúmeroO-
:QUADRADAMATRIZD)
000
000
:EXEMPLO
0.valemmatrizdaelementososTodos-
:NULAMATRIZC)
CBA
A](https://image.slidesharecdn.com/aula2-matrizes-150221113034-conversion-gate02/85/Aula-2-matrizes-10-320.jpg)
Aula 2 matrizes
Este documento apresenta os principais conceitos de matrizes em três frases: 1) Matrizes são representadas por tabelas onde cada elemento tem uma linha e coluna, permitindo operações como adição e subtração quando tiverem a mesma ordem. 2) Existem vários tipos de matrizes como quadrada, nula e identidade, e operações como transposta, oposta e multiplicação por um número. 3) A multiplicação de matrizes será explicada nas próximas aulas, com exercícios propostos de adição, subtração e multiplicação por um número.
Mais conteúdo relacionado
![MatemáTica Matrizes [TaíS Andrade]](https://cdn.slidesharecdn.com/ss_thumbnails/matemtica-matrizestasandrade-100127025923-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
![MatemáTica Matrizes [TaíS Andrade]](https://cdn.slidesharecdn.com/ss_thumbnails/matemtica-matrizestasandrade-100127025840-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Mais de João Alessandro da Luz, Secretaria de Estado da Educação do Paraná, Campo Mourão - Pr
Aula 2 matrizes
- 1. AULA 02 GEOMETRIAANALÍTICA E ÁLGEBRALINEAR Professor: João Alessandro MATRIZES
- 2.
- 3. 1.1 POSTULADOS EAXIOMAS Postulados ou Axiomas: São definições que relacionam conceitos primitivos e aceitamos sem demonstração. Exemplos: a) Existe reta, e numa reta, bem como fora dela há infinitos pontos. b) Existe plano, e num plano, bem como fora dele há infinitos pontos. Exemplo a Exemplo b
- 4. Teoremas: Propriedades quepodem ser justificadas com base nos postulados. Exemplos: a)Teorema de Pitágoras: a² = b² + c² b) Teorema Angular de Tales: O Teorema nos diz que a soma de todos os ângulos internos de um triângulo QUALQUER é igual à 1800 . 1.2 TEOREMAS
- 5. Corolário: é umadecorrência imediata de um teorema. Exemplos: o comprimento da diagonal de um quadrado cujo lado possui comprimento a é dado por . Isso é um corolário do Teorema de Pitágoras. Lema: é um teorema que é usado como um passo intermediário para atingir um resultado maior, provado em outro teorema. Normalmente o lema tem pouca serventia além de servir ao propósito do teorema que o utiliza, mas isto não é uma regra, e a classificação entre lemas e teoremas é arbitrária. 1.3 OUTROS 2a
- 6.
- 7. 2. MATRIZ Conheça eveja a tabela de Notas do 2º Ano do Ensino Médio de 2 alunos em 2013: Pois é! Vou ter quePois é! Vou ter que estudar mais este ano!!!estudar mais este ano!!! Pois é Baby... EstePois é Baby... Este ano menos Pedroano menos Pedro Paulo e Alex naPaulo e Alex na cabeça e maiscabeça e mais estudo!!!estudo!!! Maria Setembrina Rick Martini
- 8. TABELA DE NOTAS Alunos/Notas 1º Bimestre 2º Bimestre 3º Bimestre 4º Bimestre Média Anual Resultado Maria Setembrina 4060 40 60 50 Reprovada Rick Martini 20 40 30 30 30 Reprovado A IDÉIA DE MATRIZ É A IDÉIA DE UMA TABELA: PARA A MATEMÁTICA, CHAMAREMOS LINHA DE (i) E COLUNA DE (j), AMBAS COM LETRA MINÚSCULA. PORTANTO NA TABELA ACIMA TEMOS: i = 3 e j = 7
- 9.
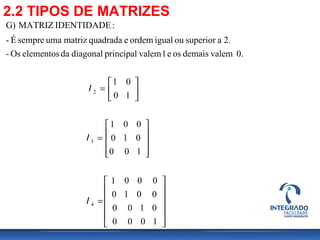
- 10. 2.2 TIPOS DEMATRIZES [ ] = = 01 4 3 :EXEMPLO AtipoDo- coluna.únicaumaPossui- :COLUNAMATRIZB) 543 :EXEMPLO AtipoDo- linha.únicaumaPossui- :LINHAMATRIZA) mx1 1xn A A [ ] = == = = 497 6815 1410 62 83 ;3 :EXEMPLO n.mPortanto colunas.denúmeroaoigualélinhasdenúmeroO- :QUADRADAMATRIZD) 000 000 :EXEMPLO 0.valemmatrizdaelementososTodos- :NULAMATRIZC) CBA A
- 11. 2.2 TIPOS DEMATRIZES = = −− −− =− − − = 12810 1043 Aatranspostmatriz 1201 84 103 :EXEMPLO colunas.pelaslinhasasnteordenadamese-trocandoobtidaÉ- :TRANSPOSTAMATRIZF) 798 543 : 798 543 :EXEMPLO A.-pordarepresentaéAdeopostamatrizA- matriz.umadeelementocadadesinalose-trocandoobtidaÉ- :OPOSTAMATRIZE) t aeA AopostaMatriz A
- 12.
- 13. 2.3 IGUALDADE DEMATRIZES ( ) BA PORTANTO BeA ba Definição ijij = − − = − − = =⇔= == : 798 543 798 543 :EXEMPLO BA :TEMOSn,xmTIPO,MESMODOMATRIZES ,bBE)(aASENDO: ijij
- 14. 2.4 ADIÇÃO DEMATRIZES ( ) :EXEMPLO BA :TEMOSn,xmTIPO,MESMODOMATRIZES ,ijbBE)ij(aASENDO: ijbijaijcC Definição +=⇔+= == −+ − 01 52 40 52 04 11 = 53 52 31 É sempre possível somar matrizes? Não! Somente quando estas forem de mesma ordem. + = Se liguem, o mesmo vale pra subtração.
- 15. 2.5 SUBTRAÇÃO DEMATRIZES ( ) −− − = −− −− = −= = = −=⇔−= == 72 54 9253 10548 :. 95 104 23 58 :EXEMPLO BA :TEMOSn,xmTIPO,MESMODOMATRIZES ,bBE)(aASENDO: ijij C C BAC PORTANTOBeA bacC Definição ijijij
- 16. 6. MULTIPLICAÇÃO DEUM NÚMERO POR UMA MATRIZ = = = = = =⇔= = 46 1016 2.23.2 5.28.2 .2 :.2 23 58 :EXEMPLO .. :TEMOSREAL, NÚMEROr UMEn,xmTIPO,DOMATRIZ ,)(aASENDO: ij B B AB PORTANTOreA arBArB Definição ijij
- 17. 2.7 MULTIPLICAÇÃO DEMATRIZES SERÁ VISTO EM QUADRO-NEGRO NAS PRÓXIMAS AULAS. AGUARDEM!!!!
- 18.
- 19. 3. EXERCÍCIOS a) A+ B b) B – A c) 2A d) B – I2
- 20.
- 21.