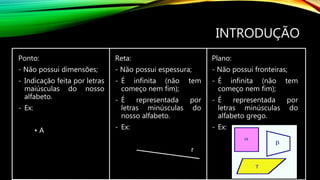
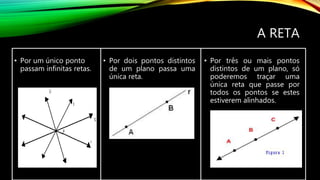
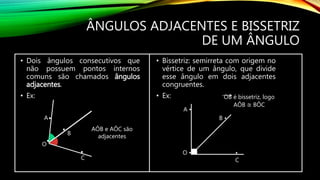
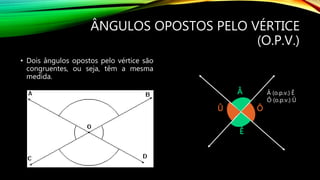
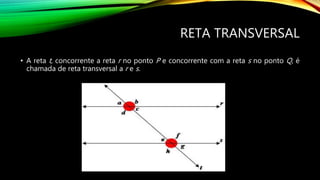
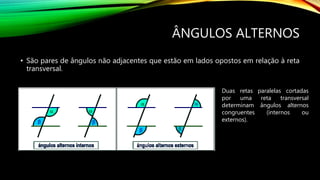
1) O documento discute conceitos básicos de geometria como retas, pontos, ângulos e suas posições relativas. 2) Apresenta as definições de reta, ponto e plano assim como tipos de ângulos como agudos, retos e obtusos. 3) Explica propriedades angulares como ângulos adjacentes, complementares e suplementares e a relação entre ângulos formados por uma reta transversal cortando duas ou mais retas paralelas.

1. GEOMETRIA: RETAS E
ÂNGULOS
Professor João Paulo Luna

2. INTRODUÇÃO
Reta:
- Não possui espessura;
- É infinita (não tem
começo nem fim);
- É representada por
letras minúsculas do
nosso alfabeto.
- Ex:
r
Ponto:
- Não possui dimensões;
- Indicação feita por letras
maiúsculas do nosso
alfabeto.
- Ex:
• A
Plano:
- Não possui fronteiras;
- É infinita (não tem
começo nem fim);
- É representada por
letras minúsculas do
alfabeto grego.
- Ex:

3. A RETA
• Por um único ponto
passam infinitas retas.
• Por dois pontos distintos
de um plano passa uma
única reta.
• Por três ou mais pontos
distintos de um plano, só
poderemos traçar uma
única reta que passe por
todos os pontos se estes
estiverem alinhados.

4. POSIÇÕES RELATIVAS DE DUAS
RETAS EM UM PLANO
• Retas Concorrentes: se cruzam em
um único ponto.
r •
s
a
b
• Retas Paralelas: não se cruzam, ou
seja, não possuem pontos comuns.
r
m
d c

5. SEMIRRETA E SEGMENTO DE RETA
• Semirreta: tem início mas não tem fim.
Inicia-se no ponto de origem, e passa
por outro ponto.
• Ex: AB
A •
• B
• Segmento de reta: tem início e tem
fim. Inicia-se em um ponto e para em
outro ponto.
• Ex: AB
A •
• B

6. PONTO MÉDIO DE UM SEGMENTO
• Um ponto M, interno a um segmento AB,
é denominado ponto médio do
segmento AB se M divide AB em dois
segmentos congruentes.
O
A • • • C
AO ≅ OC
• Este é o símbolo de congruência (≅),
significa que os dois segmentos
apresentam a mesma medida.
𝐴𝐵 = 18𝑐𝑚
𝐶𝐷 = 18𝑐𝑚
Logo:
AB ≅ CD

7. ÂNGULOS
• Denomina-se ângulo a região formada por duas semirretas que têm a mesma
origem.

8. ÂNGULOS ESPECIAIS
• Ângulo raso ou meia-volta: • Ângulo nulo (0º):
O• • •
A B
• Ângulo de uma volta (360º):

9. ÂNGULOS ESPECIAIS
Ângulo reto
med (AÔB) = 90º
Ângulo agudo
0º < med (AÔB) < 90º
Ângulo agudo
90º < med (AÔB) < 180º

10. ÂNGULOS ADJACENTES E BISSETRIZ
DE UM ÂNGULO
• Dois ângulos consecutivos que
não possuem pontos internos
comuns são chamados ângulos
adjacentes.
• Ex:
•
•
•
•
A
O
B
C
AÔB e AÔC são
adjacentes
• Bissetriz: semirreta com origem no
vértice de um ângulo, que divide
esse ângulo em dois adjacentes
congruentes.
• Ex:
A •
O •
B •
•
C
OB é bissetriz, logo
AÔB ≅ BÔC

11. ÂNGULOS COMPLEMENTARES E
SUPLEMENTARES
• Ângulos complementares: são ângulos
que somados resultam em um ângulo
reto (90º).
• Ex:
AÔB = 60º
BÔC = 30º
AÔB + BÔC → 60º + 30º = 90º
A •
B •
•
C
O •
• Ângulos suplementares: são ângulos
que somados resultam em um ângulo
raso (180º).
• Ex:
AÔB = 100º
BÔC = 80º
AÔB + BÔC → 100º + 80º = 180º
•
A
•
O
•
C
B •

12. ÂNGULOS OPOSTOS PELO VÉRTICE
(O.P.V.)
• Dois ângulos opostos pelo vértice são
congruentes, ou seja, têm a mesma
medida.
Â
Ê
ÔÛ
 (o.p.v.) Ê
Ô (o.p.v.) Û

13. RETA TRANSVERSAL
• A reta t, concorrente a reta r no ponto P e concorrente com a reta s no ponto Q, é
chamada de reta transversal a r e s.

14. ÂNGULOS CORRESPONDENTES
• São pares de ângulos não adjacentes situados em um mesmo lado da reta
transversal, um na região interna e o outro na região externa às retas r e s.
r
s
Quando r // s, temos que:
 ≅ Ê
Â
Ê

15. ÂNGULOS ALTERNOS
• São pares de ângulos não adjacentes que estão em lados opostos em relação à reta
transversal.
Duas retas paralelas cortadas
por uma reta transversal
determinam ângulos alternos
congruentes (internos ou
externos).

16. ÂNGULOS COLATERAIS
• São pares de ângulos não adjacentes localizados no mesmo lado da reta transversal.
Â
Ê
Ô
Î
Quando r // s, temos que:
 + Ê ou Ô + Î = 180º