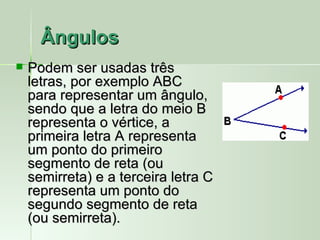
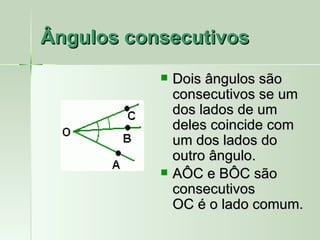
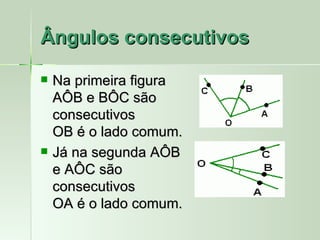
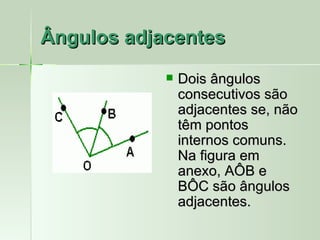
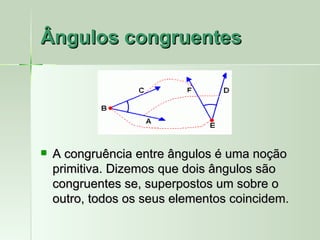
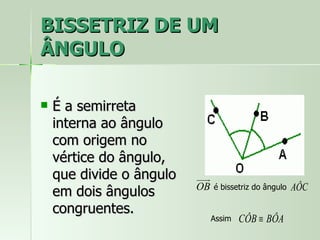
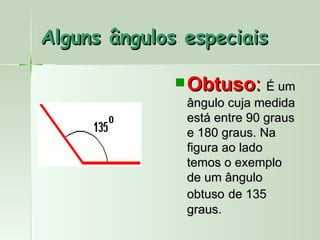
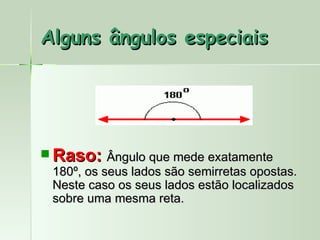
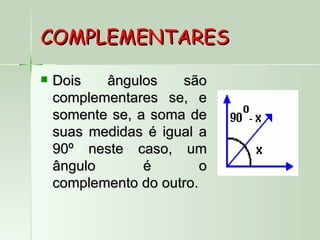
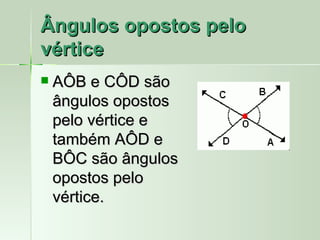
O documento define e descreve vários tipos de ângulos, incluindo: (1) ângulos são formados por dois segmentos de reta a partir de um ponto comum chamado vértice; (2) ângulos podem ser nomeados usando três letras com a letra do meio representando o vértice; (3) ângulos consecutivos compartilham um lado em comum.

1. Ângulos
 Ângulo é a reunião de dois
segmentos de reta
orientados (ou duas
semirretas orientadas) a
partir de um ponto comum.
 A interseção entre os dois
segmentos (ou semirretas) é
denominada vértice do
ângulo e os lados do ângulo
são os dois segmentos (ou
semirretas).

2. Ângulos
 Podem ser usadas três
letras, por exemplo ABC
para representar um ângulo,
sendo que a letra do meio B
representa o vértice, a
primeira letra A representa
um ponto do primeiro
segmento de reta (ou
semirreta) e a terceira letra C
representa um ponto do
segundo segmento de reta
(ou semirreta).

3. Ângulos consecutivos
 Dois ângulos são
consecutivos se um
dos lados de um
deles coincide com
um dos lados do
outro ângulo.
 AÔC e BÔC são
consecutivos
OC é o lado comum.

4. Ângulos consecutivos
 Na primeira figura
AÔB e BÔC são
consecutivos
OB é o lado comum.
 Já na segunda AÔB
e AÔC são
consecutivos
OA é o lado comum.

5. Ângulos adjacentes
 Dois ângulos
consecutivos são
adjacentes se, não
têm pontos
internos comuns.
Na figura em
anexo, AÔB e
BÔC são ângulos
adjacentes.

6. Ângulos congruentes
 A congruência entre ângulos é uma noção
primitiva. Dizemos que dois ângulos são
congruentes se, superpostos um sobre o
outro, todos os seus elementos coincidem.

7. BISSETRIZ DE UM
ÂNGULO
 É a semirreta
interna ao ângulo
com origem no
vértice do ângulo,
que divide o ângulo uuu
r
OB é bissetriz do ângulo AÔC
em dois ângulos
congruentes.
Assim CÔB ≡ BÔA

8. Alguns ângulos especiais
 Reto: Um ângulo reto é um ângulo
cuja medida é exatamente 90º.
Assim os seus lados estão
localizados em retas
perpendiculares.

9. Alguns ângulos especiais
 Agudo: Ângulo
cuja medida é
maior do que 0
graus e menor
do que 90 graus.
Ao lado temos
um ângulo de 45
graus.

10. Alguns ângulos especiais
 Obtuso: É um
ângulo cuja medida
está entre 90 graus
e 180 graus. Na
figura ao lado
temos o exemplo
de um ângulo
obtuso de 135
graus.

11. Alguns ângulos especiais
 Raso: Ângulo que mede exatamente
180º, os seus lados são semirretas opostas.
Neste caso os seus lados estão localizados
sobre uma mesma reta.

12. Ângulos
complementares,
suplementares e
replementares.

13. COMPLEMENTARES
 Dois ângulos são
complementares se, e
somente se, a soma de
suas medidas é igual a
90º neste caso, um
ângulo é o
complemento do outro.

14. SUPLEMENTARES
 Dois ângulos são suplementares se, e
somente se, a soma de suas medidas
é igual a 180º e neste caso, um
ângulo é o suplemento do outro.

15. REPLEMENTARES
 Dois ângulos são
replementares se, e
somente se, a soma
de suas medidas é
igual a 360º e neste
caso, um ângulo é o
replemento do outro.

16. Ângulos opostos pelo
vértice
 Consideremos duas retas
concorrentes cuja interseção seja
o ponto O. Essas retas
determinam quatro ângulos. Os
ângulos que não são adjacentes
são opostos pelo vértice.

17. Ângulos opostos pelo
vértice
 AÔB e CÔD são
ângulos opostos
pelo vértice e
também AÔD e
BÔC são ângulos
opostos pelo
vértice.

18. Ângulos opostos pelo
vértice
Se dois ângulos são
opostos pelo vértice,
então eles são
congruentes.

19. Ângulos
Professor: Carlinhos