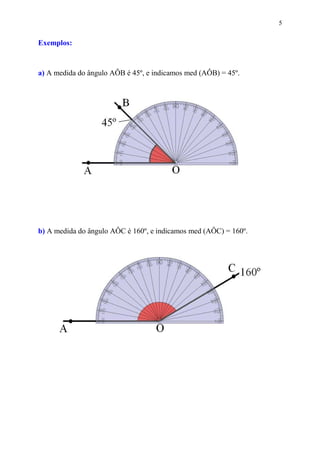
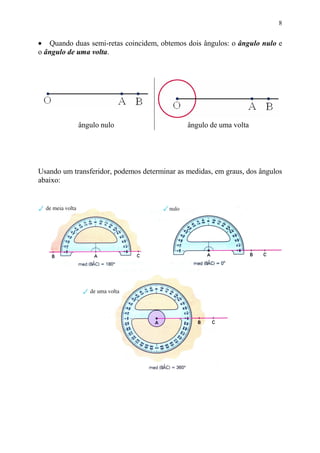
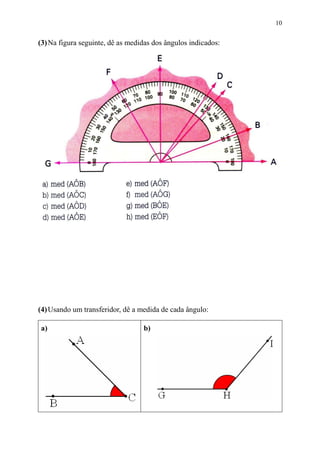
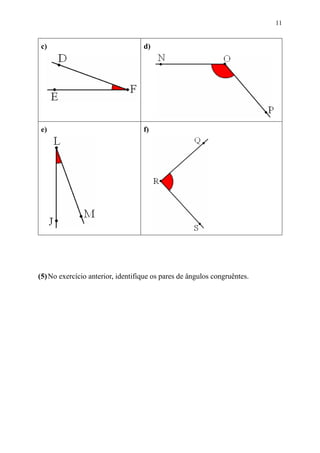
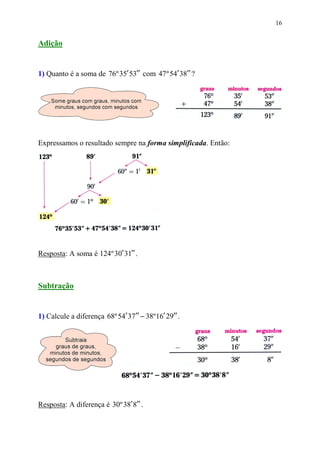
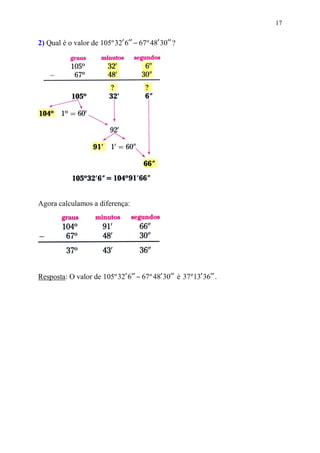
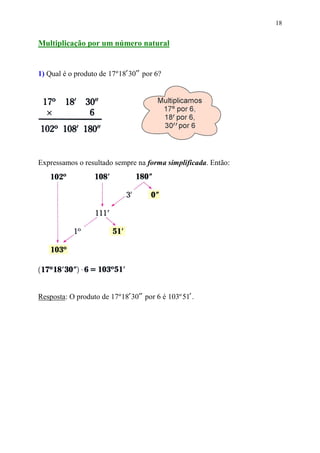
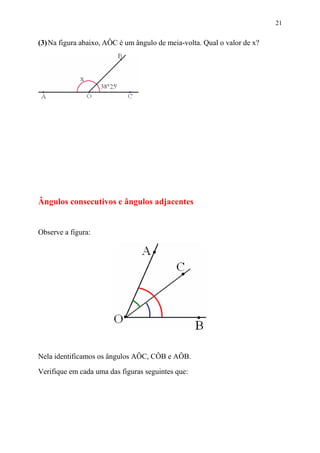
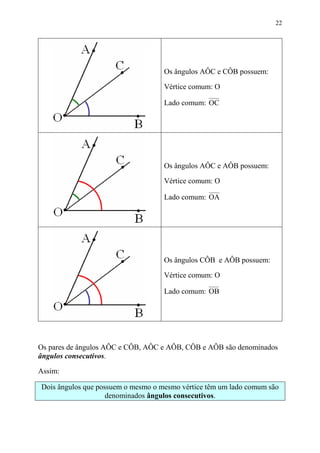
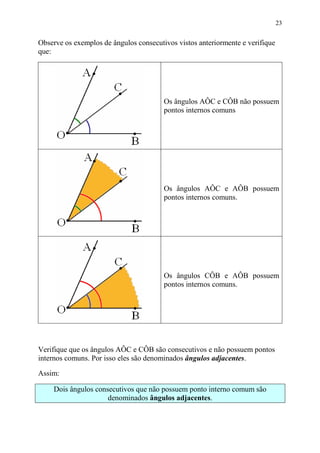
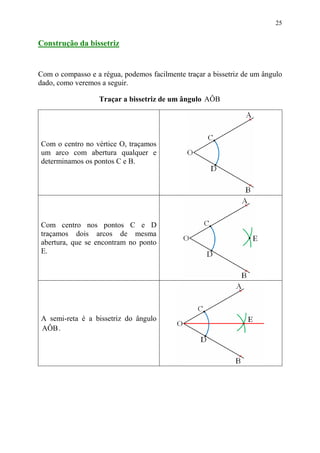
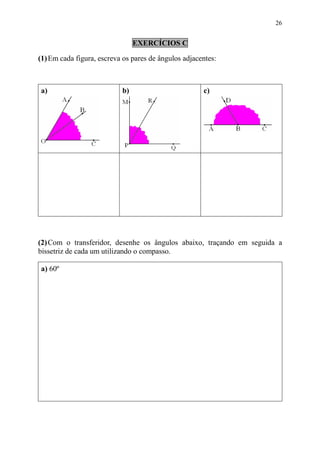
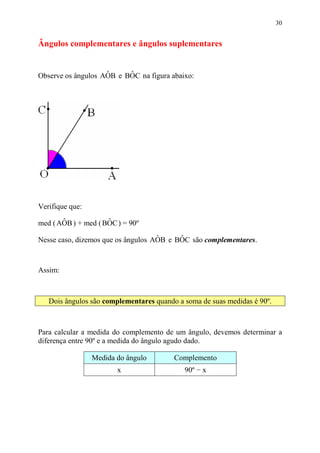
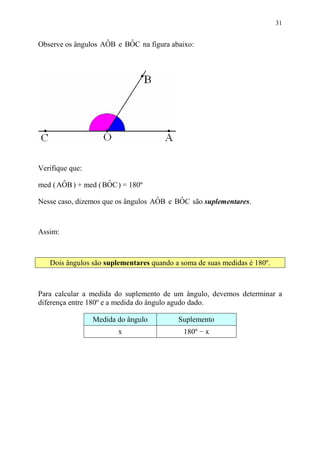
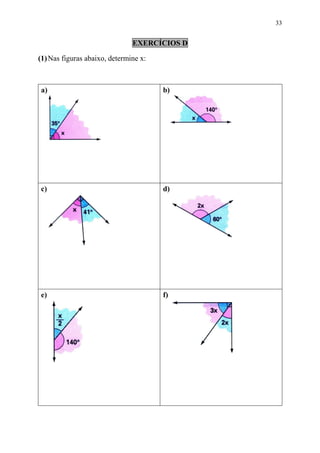
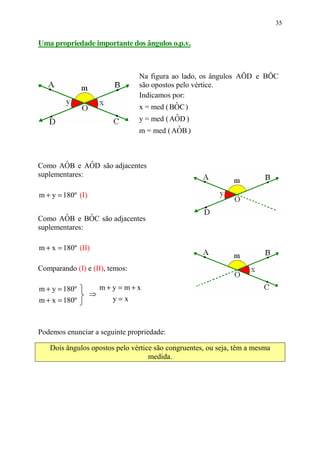
Este documento fornece informações sobre ângulos, incluindo definições, medidas, operações e propriedades. Ele discute conceitos como vértice, lados, medida em graus, minutos e segundos, ângulos congruentes, ângulos consecutivos, bissetriz e exercícios.

1. Ângulos
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
O ângulo e seus elementos.............................................................................................. 1
Medida de um ângulo...................................................................................................... 3
Ângulos congruentes ................................................................................................ 6
Ângulo raso e ângulo nulo........................................................................................ 7
Operações com medidas de ângulos ............................................................................. 13
Transformação de unidades.................................................................................... 14
Simplificando os resultados ................................................................................... 15
Adição .................................................................................................................... 16
Subtração ................................................................................................................ 16
Multiplicação por um número natural .................................................................... 18
Divisão por um número natural.............................................................................. 19
Ângulos consecutivos e ângulos adjacentes ................................................................. 21
Bissetriz de um ângulo.................................................................................................. 24
Construção da bissetriz........................................................................................... 25
Ângulo reto, ângulo agudo e ângulo obtuso ................................................................. 28
Retas perpendiculares............................................................................................. 29
Ângulos complementares e ângulos suplementares...................................................... 30
Ângulos opostos pelo vértice ........................................................................................ 34
Uma propriedade importante dos ângulos o.p.v....................................................................... 35
Referências bibliográficas............................................................................................. 38

2. 1
Ângulos
O ângulo e seus elementos
Veremos como representar matematicamente um ângulo e destacar suas partes
principais, utilizando os modelos abaixo:
Nos modelos matemáticos de figuras que surgem a idéia de ângulo, podemos
destacar duas semi-retas de mesma origem e não-opostas, que dividem o plano
em duas regiões: uma convexa e outra não-convexa.
Denominamos ângulo a região formada por duas semi-retas não-opostas que têm
a mesma origem.

3. 2
No ângulo da figura abaixo, podemos destacar os seguintes elementos:
O é o vértice do ângulo
As semi-retas OA e OB são denominadas lados do ângulo
Para identificar esse ângulo utilizamos a notação AÔB ou BÔA :
(Lê-se “ângulo AOB”)
A letra que corresponde ao vértice deve ficar no meio
OBS.: Quando não houver dúvidas quanto ao ângulo a que nos referimos,
podemos utilizar uma notação que indica apenas o seu vértice.
Ângulo Ô ou AÔB ˆ
Ângulo P ou MPN Neste caso, há três
ângulos com vértices em
O: AÔB , BÔC e AÔC

4. 3
Medida de um ângulo
A medida de um ângulo é dada pela medida de sua abertura, e a unidade padrão
utilizada é o grau, que se representa pelo símbolo º após o número.
Vamos ver o que representa o grau.
As primeiras noções de ângulo foram desenvolvidas na Grécia antiga. Deve-se a
Hiparco de Nicéia (século II a.C.), considerado pelos gregos como o pai da
Astronomia, a primeira divisão do círculo em 360 partes iguais, com o objetivo
de medir ângulos.
A cada um desses 360 arcos em que a circunferência foi dividida associamos um
ângulo cuja medida chamaremos de 1 grau.
O grau é uma unidade de medida de ângulo; 1 grau corresponde à medida do
1
ângulo (com vértice no centro da circunferência) associado a um arco de da
360
circunferência.

5. 4
Exemplos:
Assim, para medir um ângulo, comparamos sua medida à medida de um ângulo
de 1º. Ná prática, utilizamos um instrumento de medida chamado transferidor. O
transferidor já vem graduado com divisões de 1º em 1º.
Para medir um ângulo:
• coloque o transferidor sobre o ângulo, fazendo com que seu centro coincida
com o vértice do ângulo
• coloque a escala correspondente ao zero no transferidor sobre um dos lados
do ângulo
• identifique na escala do transferidor o número interceptado pelo outro lado do
ângulo

6. 5
Exemplos:
a) A medida do ângulo AÔB é 45º, e indicamos med (AÔB) = 45º.
b) A medida do ângulo AÔC é 160º, e indicamos med (AÔC) = 160º.

7. 6
Ângulos congruentes
ˆ
Consideremos os ângulos AÔB e MPQ abaixo:
Se transportarmos um ângulo sobre o outro, podemos notar que os vértices e os
lados dos dois ângulos coincidem:
ˆ
Assim, AÔB e MPQ possuem a mesma
abertura e, portanto, a mesma medida.
Dois ângulos que têm a mesma medida são chamados ângulos congruentes, e
utilizamos o símbolo ≅ para relacioná-los.
congruente
med (AÔB) = med (MPQ)
ˆ
AÔB ≅ MPQ
ˆ
usamos o símbolo =
quando comparamos
medidas usamos o símbolo ≅
quando comparamos
ângulos

8. 7
Na prática, utilizamos o transferidor para determinar se dois ângulos são ou não
congruentes.
ˆ
med (ABC) = 56º med (DÊF) = 56º
AÔB ≅ DÊF
Ângulo raso e ângulo nulo
• Quando duas semi-retas são opostas, dizemos que formam um ângulo raso ou
de meia-volta.
BÂC é um ângulo raso ou de meia-volta

9. 8
• Quando duas semi-retas coincidem, obtemos dois ângulos: o ângulo nulo e
o ângulo de uma volta.
ângulo nulo ângulo de uma volta
Usando um transferidor, podemos determinar as medidas, em graus, dos ângulos
abaixo:

10. 9
EXERCÍCIOS A
(1) Considere o ângulo da figura abaixo e responda:
a) Qual é o vértice desse ângulo?
b) Quais são os lados desse ângulo?
c) Qual é o nome desse ângulo?
(2) Na figura abaixo, identifique todos os ângulos e nomei os mesmos.

11. 10
(3) Na figura seguinte, dê as medidas dos ângulos indicados:
(4) Usando um transferidor, dê a medida de cada ângulo:
a) b)

12. 11
c) d)
e) f)
(5) No exercício anterior, identifique os pares de ângulos congruêntes.

13. 12
(6) Construa, com a ajuda do transferidor, um ângulo de:
a) 42º
b) 90º
c) 125º
d) 180º

14. 13
Operações com medidas de ângulos
Como vimos, o transferidor mede ângulos com intervalos de 1 em 1 grau. Mas
há ângulos que não possuem como medida um número inteiro de graus. Como
não é costume utilizar decimais em medidas de ângulos, utilizamos os
submúltiplos do grau.
O grau tem dois submúltiplos: o minuto e o segundo. Para escrever a medida de
um ângulo utilizando o minuto e o segundo, utilizamos a base 60 de numeração.
• minuto → símbolo : ′
• segundo → símbolo : ′′
Portanto:
Por exemplo, o ângulo de medida 18,5º pode ser escrito assim:
18,5º = 18º + 0 ,5º = 18º + 30′ = 18º 30′

15. 14
Transformação de unidades
Vejamos como fazer transformações de unidades de ângulos observando os
exemplos:
1) Quantos minutos tem 32º?
Resposta: 32º tem 1920′ .
2) Expresse 2º 7′ 30′′ em segundos.
Resposta: 2º 7′ 30′′ tem 7650′′ .
3) Escreva 5680′′ em graus, minutos e segundos.
Resposta: 5680′′ tem 1º 34′ 40′′ .

16. 15
Simplificando os resultados
Em algumas situações, principalmente nas operações com medidas de ângulos,
precisamos simplificar os resultados obtidos. Vejamos como fazer isso,
observando os exemplos.
1) Simplificar 54º 60′ .
54º 60′ = 54º + 1º = 55º
Resposta: 54º 60′ escrito na forma simplificada é 55º.
2) Simplificar 18º 126′ .
18º 126′ = 18º + 120′ + 6′ = 18º + 2º + 6′ = 20º + 6′ = 20º 6′
Resposta: 18º 126′ escrito na forma simplificada é 20º 6′ .
3) Simplificar 27 º 75′ 80′′ .
27º 75′ 80′′ = 27º + 75′ + 80′′
27º 75′ 80′′ = 27º + 75′ + 60′′ + 20′′
27º 75′ 80′′ = 27º + 75′ + 1′ + 20′′
27º 75′ 80′′ = 27º + 76′ + 20′′
27º 75′ 80′′ = 27º + 60′ + 16′ + 20′′
27º 75′ 80′′ = 27º + 1º +16′ + 20′′
27º 75′ 80′′ = 28º +16′ + 20′′
Resposta: 27 º 75′ 80′′ escrito na forma simplificada é 28º +16′ + 20′′ .

17. 16
Adição
1) Quanto é a soma de 76º 35′ 53′′ com 47 º 54′ 38′′ ?
Expressamos o resultado sempre na forma simplificada. Então:
Resposta: A soma é 124º 30′ 31′′ .
Subtração
1) Calcule a diferença 68º 54′ 37′′ − 38º 16′ 29′′ .
Resposta: A diferença é 30º 38′ 8′′ .

18. 17
2) Qual é o valor de 105º 32′ 6′′ − 67 º 48′ 30′′ ?
Agora calculamos a diferença:
Resposta: O valor de 105º 32′ 6′′ − 67 º 48′ 30′′ é 37 º 13′ 36′′ .

19. 18
Multiplicação por um número natural
1) Qual é o produto de 17 º 18′ 30′′ por 6?
Expressamos o resultado sempre na forma simplificada. Então:
Resposta: O produto de 17 º 18′ 30′′ por 6 é 103º 51′ .

20. 19
Divisão por um número natural
1) Calcule o quociente ( 82º 31′ 40′′ ) : 4.
Resposta: O quociente é 20º 37′ 55′′ .

21. 20
EXERCÍCIOS B
(1) Efetue as operações indicadas:
a) 13º 12′ + 41º 10′ 20′′ c) (27 º 36′ 33′′) :3
b) 35º 20′ − 10º 15′ 30′′ d) 4 ⋅ (10º 24′ 45′′)
(2) Determine, na forma mais simplificada possível, o valor das expressões:
a) 15º 12′ 35′′ + 27 º 18′ + 13º 51′ 30′′ b) (50º − 15º 20′) :5

22. 21
(3) Na figura abaixo, AÔC é um ângulo de meia-volta. Qual o valor de x?
Ângulos consecutivos e ângulos adjacentes
Observe a figura:
Nela identificamos os ângulos AÔC, CÔB e AÔB.
Verifique em cada uma das figuras seguintes que:

23. 22
Os ângulos AÔC e CÔB possuem:
Vértice comum: O
Lado comum: OC
Os ângulos AÔC e AÔB possuem:
Vértice comum: O
Lado comum: OA
Os ângulos CÔB e AÔB possuem:
Vértice comum: O
Lado comum: OB
Os pares de ângulos AÔC e CÔB, AÔC e AÔB, CÔB e AÔB são denominados
ângulos consecutivos.
Assim:
Dois ângulos que possuem o mesmo o mesmo vértice têm um lado comum são
denominados ângulos consecutivos.

24. 23
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique
que:
Os ângulos AÔC e CÔB não possuem
pontos internos comuns
Os ângulos AÔC e AÔB possuem
pontos internos comuns.
Os ângulos CÔB e AÔB possuem
pontos internos comuns.
Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos
internos comuns. Por isso eles são denominados ângulos adjacentes.
Assim:
Dois ângulos consecutivos que não possuem ponto interno comum são
denominados ângulos adjacentes.

25. 24
Bissetriz de um ângulo
Observe a figura abaixo:
med ( AÔP ) = med ( PÔB ) = 25º
Verifique que a semi-reta OP divide o
ângulo AÔB em dois ângulos ( AÔP e
PÔB ) congruentes.
Nesse caso, a semi-reta OP é
denominada bissetriz do ângulo AÔB .
Assim:
Bissetriz de um ângulo é a semi-reta de origem no vértice desse ângulo que
determina, com seus lados, dois ângulos adjacentes congruentes.

26. 25
Construção da bissetriz
Com o compasso e a régua, podemos facilmente traçar a bissetriz de um ângulo
dado, como veremos a seguir.
Traçar a bissetriz de um ângulo AÔB
Com o centro no vértice O, traçamos
um arco com abertura qualquer e
determinamos os pontos C e B.
Com centro nos pontos C e D
traçamos dois arcos de mesma
abertura, que se encontram no ponto
E.
A semi-reta é a bissetriz do ângulo
AÔB .

27. 26
EXERCÍCIOS C
(1) Em cada figura, escreva os pares de ângulos adjacentes:
a) b) c)
(2) Com o transferidor, desenhe os ângulos abaixo, traçando em seguida a
bissetriz de cada um utilizando o compasso.
a) 60º

28. 27
b) 110º
c) 90º
d) 77º

29. 28
Ângulo reto, ângulo agudo e ângulo obtuso
Podemos classificar um ângulo em agudo, obtuso ou reto.
Ângulo reto é o ângulo cuja
medida é 90º.
Ângulo agudo é o ângulo cuja
medida é menor que 90º.
Ângulo obtuso é o ângulo cuja
medida é maior que 90º.

30. 29
Retas perpendiculares
Se traçarmos duas retas num plano, tais que sejam concorrentes (possuam um
ponto em comum), é possível obter 4 ângulos congruentes, ou seja, de mesma
medida.
É fácil verificar que cada um desses ângulos
mede 90º.
a=b=c=d
Quando duas retas concorrentes formam entre si quatro ângulos retos, dizemos
que as retas são perpendiculares e utilizamos o símbolo ⊥ para representar esse
perpendicularismo.
Na figura ao lado, r e s formam entre si quatro
ângulos retos; então r ⊥ s .
Símbolo: ⊥ (perpendicular a)

31. 30
Ângulos complementares e ângulos suplementares
ˆ ˆ
Observe os ângulos AOB e BOC na figura abaixo:
Verifique que:
ˆ ˆ
med ( AOB ) + med ( BOC ) = 90º
ˆ ˆ
Nesse caso, dizemos que os ângulos AOB e BOC são complementares.
Assim:
Dois ângulos são complementares quando a soma de suas medidas é 90º.
Para calcular a medida do complemento de um ângulo, devemos determinar a
diferença entre 90º e a medida do ângulo agudo dado.
Medida do ângulo Complemento
x 90º − x

32. 31
ˆ ˆ
Observe os ângulos AOB e BOC na figura abaixo:
Verifique que:
ˆ ˆ
med ( AOB ) + med ( BOC ) = 180º
ˆ ˆ
Nesse caso, dizemos que os ângulos AOB e BOC são suplementares.
Assim:
Dois ângulos são suplementares quando a soma de suas medidas é 180º.
Para calcular a medida do suplemento de um ângulo, devemos determinar a
diferença entre 180º e a medida do ângulo agudo dado.
Medida do ângulo Suplemento
x 180º − x

33. 32
Exemplos:
a) Determinar a medida do complemento e do suplemento do ângulo de 46º.
Complemento: 90º −46º = 44º
Suplemento: 180º −46º = 134º
Resposta: O complemento do ângulo de 46º mede 44º e o suplemento 134º.
b) Na figura abaixo, determinar o valor de x.
Como os ângulos são adjacentes complementares:
x + 30º + x − 10º = 90º
2x + 20º = 90º
2 x = 90º − 20º
2x = 70º
70º
x=
2
x = 35º
Resposta: O valor de x é 35º.
ˆ ˆ
c) Na figura abaixo, determinar as medidas ABC e CBD .
Como os ângulos são adjacentes
suplementares:
3x + x + 12º = 180º
4x + 12º = 180º
4 x = 180º −12º
4x = 168º
168º
x=
4
x = 42º
ˆ ˆ
Resposta: ABC mede 126º e CBD mede 54º.

34. 33
EXERCÍCIOS D
(1) Nas figuras abaixo, determine x:
a) b)
c) d)
e) f)

35. 34
Ângulos opostos pelo vértice
Observe os ângulos AÔB e CÔD na figura abaixo:
Verifique que:
OA e OC são semi-retas opostas
OB e OD são semi-retas opostas
Portanto, as semi-retas OA e OB que formam os lados do ângulo AÔB são
opostas, respectivamente, às semi-retas OC e OD que formam os lados do
ângulo CÔD .
Neste caso, podemos também afirmar que os lados do ângulo AÔB são
formados pelos prolongamentos dos lados do ângulo CÔD , e vice-versa.
A esses dois ângulos damos o nome de ângulos opostos pelo vértice.
Dois ângulos são chamados opostos pelo vértice (abreviamos o.p.v.) quando os
lados de um forem prolongamentos dos lados do outro e vice-versa.

36. 35
Uma propriedade importante dos ângulos o.p.v.
Na figura ao lado, os ângulos AÔD e BÔC
são opostos pelo vértice.
Indicamos por:
ˆ
x = med ( BOC )
ˆ
y = med ( AOD )
ˆ
m = med ( AOB )
ˆ ˆ
Como AOB e AOD são adjacentes
suplementares:
m + y = 180º (I)
ˆ ˆ
Como AOB e BOC são adjacentes
suplementares:
m + x = 180º (II)
Comparando (I) e (II), temos:
m + y = 180º m+y = m+x
⇒
m + x = 180º y=x
Podemos enunciar a seguinte propriedade:
Dois ângulos opostos pelo vértice são congruentes, ou seja, têm a mesma
medida.

37. 36
Exemplo:
► Determinar os valores de x e y na figura abaixo.
x = 30º → ângulos o.p.v.
y + 30º = 180º → ângulos adjacetes suplementares
y = 180º − 30º
y = 150º
Resposta: O valor de x é 30º e de y é 150º.
EXERCÍCIOS E
(1) Nas figuras seguintes, calcule as medidas de x, y, a e b:
a)

38. 37
b)
c)
d)

39. 38
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
EDUCOM: ASSOCIAÇÃO PORTUGUESA DE TELEMÁTICA
EDUCATIVA. Disponível em: <http://portal.educom.pt>. Acesso em: 19 de
outubro de 2008.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
GUELLI, Oscar. Matemática: uma aventura do pensamento. São Paulo:
Ática, 1998.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
KLICK EDUCAÇÃO: O PORTAL DA EDUCAÇÃO. Disponível em:
<http://www.klickeducacao.com.br>. Acesso em: 7 de outubro de 2008.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.
MORI, Iracema; ONAGA, Dulce Onaga. Matemática: idéias e desafios. São
Paulo: Saraiva, 1997.

40. 39
MUNDO VESTIBULAR. Disponível em: <http://www.mundovestibular.com.br>.
Acesso em: 30 de outubro de 2008.
SÓ MATEMÁTICA. Disponível em: <http://www.somatematica.com.br>.
Acesso em: 23 de outubro de 2008.