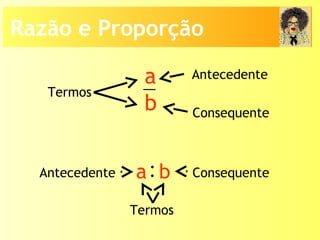
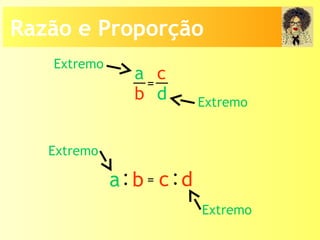
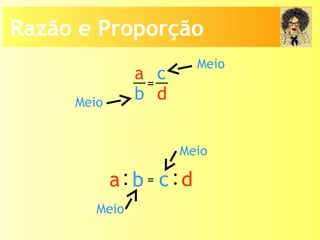
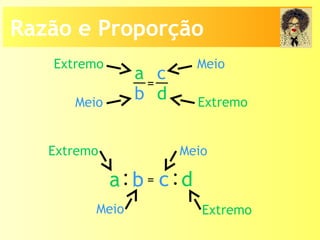
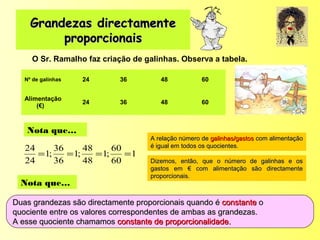
O documento descreve os conceitos de razão, proporção e as relações entre grandezas direta e inversamente proporcionais. Explica que uma razão é o quociente entre dois números e uma proporção é uma igualdade entre duas razões. Também apresenta exemplos de como calcular termos faltantes em proporções e aplicar os conceitos em situações reais.

1. Razão e Proporção

2. Razão e Proporção
A palavra razão, significa quociente, divisão,
a noção que a matemática assimilou. Por
isso, razão é o quociente entre dois
números A e B, com B ≠ 0. Assim,
a razão entre os números A e B pode ser
dita "razão de A para B" e representada
como:

3. a
b
:a b
Razão e Proporção

4. a
b
Termos
Termos
:a b
Razão e Proporção

5. a
b
Antecedente
Antecedente :a b
Razão e Proporção

6. a
b Consequente
Consequente:a b
Razão e Proporção

7. a
b
Termos
Antecedente
Consequente
Termos
Antecedente Consequente:a b
Razão e Proporção

8. Exemplo
• Uma orquestra é formada por 40 homens e 30 mulheres.
• Qual a razão entre o número de homens e o número de mulheres?Qual a razão entre o número de homens e o número de mulheres?
30
40
• Qual a razão entre o número deQual a razão entre o número de
mulheres e o número de homens?mulheres e o número de homens?
40
30
Numa razão é muito importante verificar a ordemNuma razão é muito importante verificar a ordem
pela qual estão referidas as duas grandezaspela qual estão referidas as duas grandezas

9. Uma proporção é uma igualdade entre duas razões.
Definição:
Razão e Proporção

10. Uma proporção é uma igualdade entre duas razões.
lê-se
“a está para b assim como c está para d”…
Definição:
a
b
c
d
=
Razão e Proporção

11. Uma proporção é uma igualdade entre duas razões.
lê-se
“a está para b assim como c está para d”…
…onde a, b, c e d são os termos da proporção: a
e d são extremos e b e c são os meios.
Definição:
a
b
c
d
=
Razão e Proporção

12. a
b
c
d
=
:a b :c d=
Razão e Proporção

13. Extremo
a
b
c
d
=
Extremo
:a b :c d=
Extremo
Extremo
Razão e Proporção

14. Meio
a
b
c
d
=
Meio
:a b :c d=
Meio
Meio
Razão e Proporção

15. Meio
Extremo
a
b
c
d
=
Extremo
Meio
:a b :c d=
Extremo
Extremo Meio
Meio
Razão e Proporção

16. Grandezas directamenteGrandezas directamente
proporcionaisproporcionais
Nº de galinhas 24 36 48 60
Alimentação
(€)
24 36 48 60
O Sr. Ramalho faz criação de galinhas. Observa a tabela.
1
60
60
;1
48
48
;1
36
36
;1
24
24
====
Nota que…
A relação número deA relação número de galinhas/gastosgalinhas/gastos com alimentaçãocom alimentação
é igual em todos os quocientes.é igual em todos os quocientes.
Dizemos, então, que o número de galinhas e osDizemos, então, que o número de galinhas e os
gastos em € com alimentação são directamentegastos em € com alimentação são directamente
proporcionais.proporcionais.
Duas grandezas são directamente proporcionais quando éDuas grandezas são directamente proporcionais quando é constanteconstante oo
quociente entre os valores correspondentes de ambas as grandezas.quociente entre os valores correspondentes de ambas as grandezas.
A esse quociente chamamosA esse quociente chamamos constante de proporcionalidade.constante de proporcionalidade.
Nota que…

17. Propriedade fundamental das
proporções:
Numa proporção, o produto dos meios é igual
ao produto dos extremos.
Razão e Proporção

18. Propriedade fundamental das
proporções:
Numa proporção, o produto dos meios é igual
ao produto dos extremos.
a
b
c
d
= b c× a d×=
Razão e Proporção

19. Propriedade fundamental das
proporções:
Numa proporção, o produto dos meios é igual
ao produto dos extremos.
a
b
c
d
= b c× a d×=
Meio
Meio
Razão e Proporção

20. Propriedade fundamental das
proporções:
Numa proporção, o produto dos meios é igual
ao produto dos extremos.
a
b
c
d
= b c× a d×=
Extremo
Extremo
Razão e Proporção

21. Propriedade fundamental das
proporções:
Numa proporção, o produto dos meios é igual
ao produto dos extremos.
a
b
c
d
= b c× a d×=
Meio
Extremo
Extremo
Meio
Razão e Proporção

22. Razão e Proporção
Exemplos:

23. Razão e Proporção
Exemplos:
4 12
4 21 7 12
7 21
= ⇔ × = ×

24. Exemplos:
4 12
4 21 7 12
7 21
= ⇔ × = × É proporção
Razão e Proporção

25. Exemplos:
4 12
4 21 7 12
7 21
= ⇔ × = ×
3 12
3 40 8 12
8 40
= ⇔ × ≠ ×
É proporção
Razão e Proporção

26. Exemplos:
4 12
4 21 7 12
7 21
= ⇔ × = ×
3 12
3 40 8 12
8 40
= ⇔ × ≠ ×
É proporção
Não é proporção
Razão e Proporção

27. Exercícios de aplicaçãoExercícios de aplicação
1. Descubra o termo que falta em cada uma das proporções:
?
6
3
2
=
20
25
?
5
=

28. Fica assim:
2 x ? = 3 x 6
2 x ? = 18
? = 18 : 2
? = 9
5 x 20 = ? x 25
100 = ? X 25
? = 100 : 25
? = 4
2. A idade do Rui está para a da avó assim como 2 está para 9.
O Rui tem 12 anos. Que idade tem a avó?

29. Fica assim:
?
12
9
2
=
2 x ? = 9 x 12
2 x ? = 108
? = 108 : 2
? = 54

30. Grandezas Diretamente Proporcionais
• É um tipo de proporção que envolve
duas grandezas e quando uma delas é
aumentada a outra também aumenta na
mesma proporção ou diminuindo uma
delas a outra também diminui na
mesma proporção.

31. Grandezas Diretamente Proporcionais
• Sendo duas grandezas A e B
diretamente proporcionais, então, a
relação estabelecida entre elas é:
• A/B = K ou A = B.K.

32. Exemplo: deslocamento e tempo
• Um objeto em movimento constante faz
certo deslocamento em certo tempo. Veja
abaixo uma tabela que relaciona um caso com
estas grandezas:
deslocamento(x) 3m 6m 9m 12m 15m
tempo (y)
1s 2s 3s 4s 5s

33. Exemplo: deslocamento e tempo

34.
Testando a aprendizagem...
• Verifique se as grandezas abaixo são
diretamente proporcionais e qual é a
constante de proporção entre x e y:
x 9 12 15 18
y 3 4 5 6

35. Grandezas Inversamente Proporcionais
• É o tipo de proporção que envolve duas
grandezas e quando uma delas aumenta
a outra diminui na mesma proporção ou
diminuindo uma delas a outra aumenta
na mesma proporção.

36. Grandezas Inversamente Proporcionais
• Sendo duas grandezas A e B
inversamente proporcionais, então, a
relação estabelecida entre elas é:
• A.B = K ou A = K/B

37. Exemplo: velocidade e tempo
• Neste exemplo iremos tratar das
grandezas velocidade e tempo. Primeiro,
perceba que se existe uma distância a ser
percorrida, quanto maior a
velocidade, menor é o tempo levado.

38. Exemplo: velocidade e tempo
• Veja abaixo uma tabela que relaciona o
tempo (y) total em horas de uma
viagem feita à uma velocidade (x) em
quilômetros por hora:
Velocidade (x) 60 80 100 120
Tempo (y) 4 33 ,2 4 2

39. Exemplo: velocidade e tempo
• Perceba que quando dobramos a velocidade
de 60 para 120, o tempo em horas cai de 4 para 2, ou
seja, pela metade.
• Para ter certeza de que x e y são inversamente
proporcionais, o produto deles deve ser constante:
• 60 4=240 80 3=240⋅ ⋅
100 2,4=240 120 2=240⋅ ⋅
Esta constante, neste caso, representa a distância total
percorrida na viagem.

40.
Testando a aprendizagem
• Verifique se as grandezas abaixo são
inversamente proporcionais e qual é a
constante de proporção.
x 5 10 20
y 2 1 ,0 5

41. Fim!