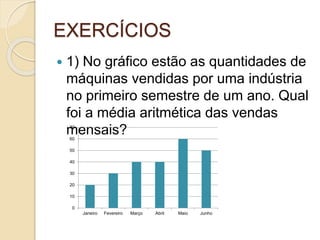
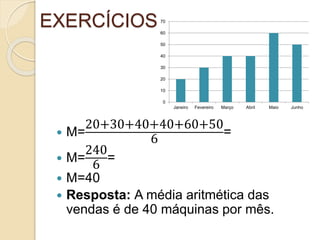
O documento apresenta os conceitos de média aritmética e média ponderada. A média aritmética é calculada somando-se os valores e dividindo-se pela quantidade de itens. A média ponderada multiplica-se cada valor pelo seu peso antes de somar e dividir. Exemplos ilustram o cálculo de médias e exercícios são propostos para treino.

1. MATEMÁTICA
AULA 3 – MÉDIAS

2. MÉDIA ARITMÉTICA
 A média aritmética de n números reais é
o número que se obtém somando os n
números e dividindo o resultado por n.
◦ EXEMPLO:
 A professora Eliete, de Português,
calculou as médias de seus alunos no
primeiro bimestre usando o seguinte
critério: somou as notas de três provas
com a nota de um trabalho e dividiu o
resultado por 4.
 Alexandre, que tirou 6,0, 4,5 e 7,0 nas
provas, e 7,5 no trabalho, ficou com que
média?

3. MÉDIA ARITMÉTICA
◦ EXEMPLO:
 Alexandre, que tirou 6,0, 4,5 e 7,0 nas
provas, e 7,5 no trabalho, ficou com que
média?

6+4,5+7+7,5
4
=

25
4
=
 6,25
 Ficou com 6,25. Essa média chama-se
média aritmética das notas.

4. MÉDIA PONDERADA
 A média ponderada de n números reais é o
número que se obtém multiplicando cada
número pelo seu peso, somando esses
produtos, e dividindo o resultado pela soma
dos pesos.
◦ EXEMPLO:
 O professor Maurício, de Matemática,
aplicou duas provas e propôs dois
trabalhos. A média bimestral foi calculada
assim: somou as notas de cada trabalho,
multiplicadas por 2, com as notas de cada
prova, multiplicadas por 3, e dividiu o

5. MÉDIA PONDERADA
◦ EXEMPLO:
 Alexandre tirou 6,0 e 7,0 nos trabalhos e
obteve 4,0 e 5,0 nas provas. Com que
média ficou?

6.2+7.2+4.3+5.3
10
=

12+14+12+15
10
=
53
10
 5,3
 O número 10, denominador da fração
acima, é a soma dos pesos atribuídos a
cada avaliação: 2 + 2 + 3 + 3 = 10 .

6. OBSERVAÇÕES
 A média aritmética é uma média
ponderada em que todos os valores
têm o mesmo peso.
◦ EXEMPLO:
◦ Num supermercado trabalham quatro
supervisores (ganhando cada um R$
1.250,00 por mês), vinte caixas
(ganhando cada um R$ 750,00 por mês)
e quarenta auxiliares (ganhando cada um
R$ 300,00 por mês). Em média, quanto
ganha cada um desses empregados?

7. OBSERVAÇÕES
◦ EXEMPLO:
◦ Queremos a média aritmética de 4
números iguais a 1.250, 20 iguais a 750 e
40 iguais a 300. O denominador será 64,
que é a soma de todos os trabalhadores.
Logo:
◦
4.1250+20.750+40.300
4+20+40
=
◦
5000+15000+12000
64
=
◦
32000
64
=500

8. OBSERVAÇÕES
 A média pode ser um número que não
ocorre na realidade. Veja esse
exemplo:
 Luana tem 3 irmãos, Danilo tem 4 e
Paola tem apenas 1. Quantos irmãos
eles tem, em média?
◦
3+4+1
3
=
◦
8
3
≈2,67
◦ Em média cada um tem 2,67 irmãos. A
afirmação é correta, mesmo que ninguém
possa ter 2,67 irmãos.

9. EXERCÍCIOS
 1) No gráfico estão as quantidades de
máquinas vendidas por uma indústria
no primeiro semestre de um ano. Qual
foi a média aritmética das vendas
mensais?
0
10
20
30
40
50
60
70
Janeiro Fevereiro Março Abril Maio Junho

10. EXERCÍCIOS
 M=
20+30+40+40+60+50
6
=
 M=
240
6
=
 M=40
 Resposta: A média aritmética das
vendas é de 40 máquinas por mês.
0
10
20
30
40
50
60
70
Janeiro Fevereiro Março Abril Maio Junho

11. EXERCÍCIOS
 2) Durante um bimestre, o professor
Humberto atribui a cada aluno 4 notas
de 0 a 10. A média bimestral é a
média aritmética das 4 notas. Com
três notas conhecidas, cuja média
aritmética é 6,0, Bia está fazendo uma
previsão de sua média bimestral. Qual
será essa média, no mínimo? E no
máximo?

12. EXERCÍCIOS
 Mínimo
 M=
6+6+6+0
4
=
 M=
18
4
=4,5
 Máximo
 M=
6+6+6+10
4
=
 M=
28
4
=7
 Resposta: A média mínima será 4,5 e a
máxima 7.

13. EXERCÍCIOS
 3) O maço da alface era vendido em
janeiro por R$ 0,70 e em fevereiro,
devido às chuvas, por R$ 1,00. Em
janeiro, a quantidade de alface
vendida foi o dobro da de fevereiro.
Em média, por quanto cada maço foi
vendido nesse período?

14. EXERCÍCIOS
 Nesse caso temos uma média
ponderada, já que existe pesos diferentes
para cada item. O preço de Janeiro tem
peso 2, já que a quantidade vendida foi o
dobro da quantidade de fevereiro, que
terá peso 1. Assim:
 M=
2.0,70+1.1,00
3
=
 M=
2,4
3
 M=0,80
 Resposta: O maço será vendido, em
média, por R$0,80.

15. EXERCÍCIOS
 4) Em certo dia, a cotação do dólar
fechou da seguinte forma:
 câmbio turismo ............................ R$
2,00
 câmbio comercial ........................ R$
1,90
 Comprando-se, neste dia, 2.000
dólares para uma viagem, 60% deles
ao câmbio turismo e 40% ao câmbio
comercial, quanto se paga em média

16. EXERCÍCIOS
 Mais um caso de média ponderada. O
cambio turismo terá peso 60, enquanto o
paralelo terá peso 40 (60% e 40%
comprados de cada tipo, respectivamente).
O denominador será 100, que é a soma dos
pesos. Assim:
 M=
60.2,00+40.1,90
100
=
 M=
120,00+76,00
100
 M=
196,00
100
 M=1,96

17. EXERCÍCIOS
 5) Num curso de inglês são aplicadas
três provas: a primeira com peso 2, a
segunda com peso 3 e a terceira com
peso 5. Além disso, o aluno pode
fazer uma prova substitutiva, que
entra no lugar de qualquer uma das
três e mantém o peso da prova
substituída. Um aluno que tirou,
respectivamente, notas 4,0, 5,0 e 6,0
e, na substitutiva, 7,6, que nota deve
substituir para ficar com a maior
média?

18. EXERCÍCIOS
 Mais um caso de média ponderada. A primeira
nota tem peso 2, a segunda 3 e a terceira 5. O
denominador será 10, que é a soma dos pesos.
 Serão necessários três cálculos para
encontrarmos a resposta, substituindo cada um
das três notas para ver em qual delas a média
será maior. Assim:
 Substituindo a Primeira Nota: 4,0 por 7,6
 M=
2.7,6+3.5,0+5.6,0
10
=
 M=
15,2+15+30
10
 M=
60,8
10
 M=6,02
 Substituindo a primeira nota a média será 6,02.

19. EXERCÍCIOS
 Substituindo a Segunda Nota: 5,0 por
7,6
 M=
2.4,0+3.7,6+5.6,0
10
=
 M=
8+22,8+30
10
 M=
60,8
10
 M=6,08
 Substituindo a segunda nota a média
será 6,08.

20. EXERCÍCIOS
 Substituindo a Terceira Nota: 6,0 por 7,6
 M=
2.4,0+3.5,0+5.7,6
10
=
 M=
8+15+38
10
 M=
61
10
 M=6,10
 Substituindo a terceira nota a média será
6,10.
 Resposta: Deve substituir a Terceira