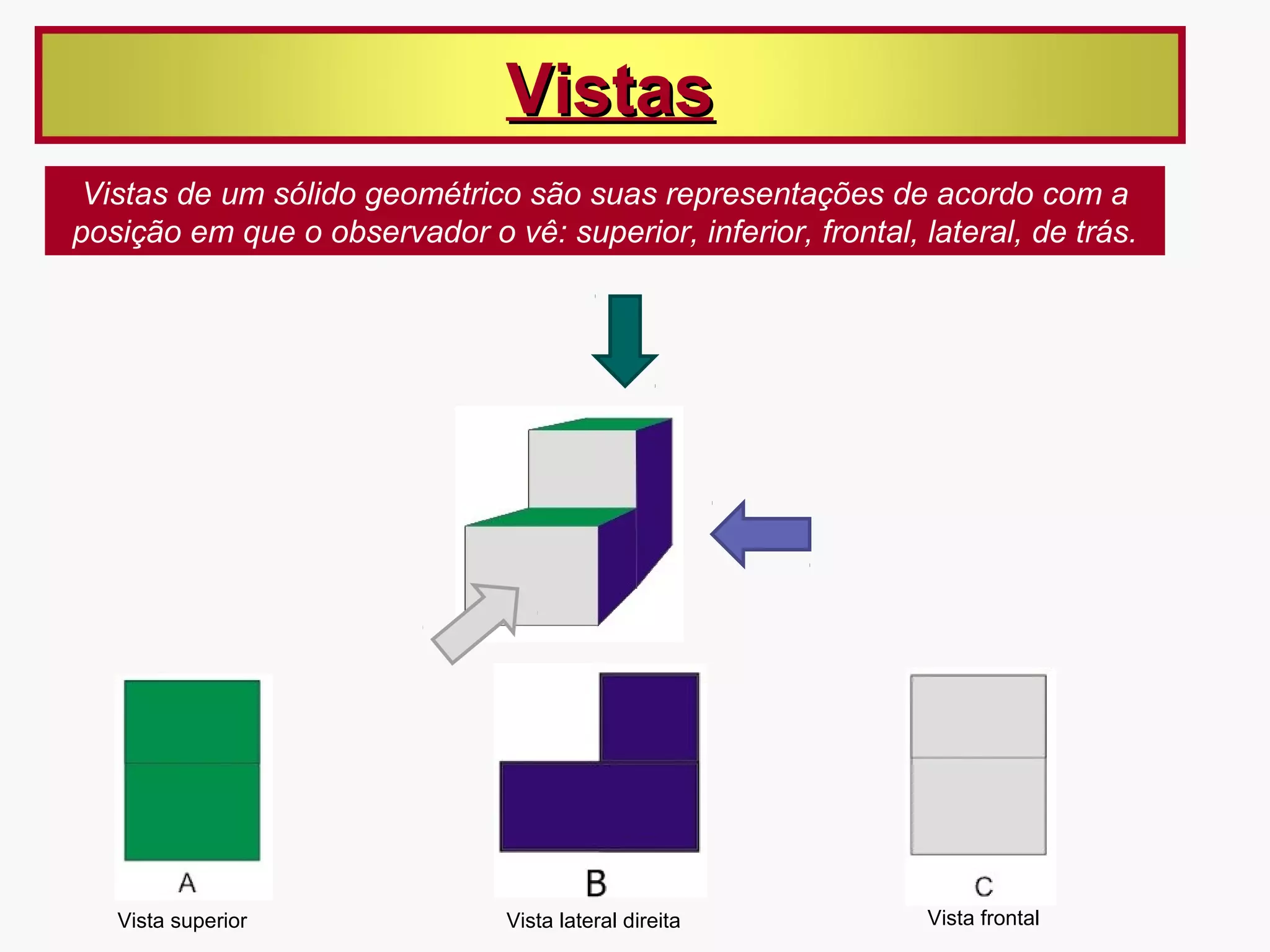
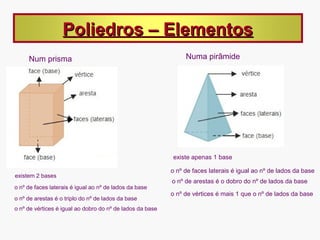
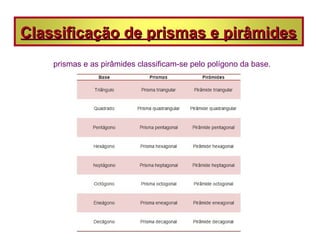
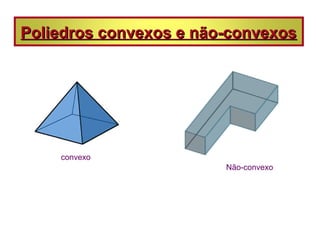
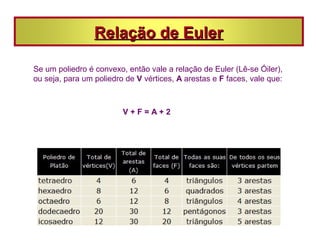
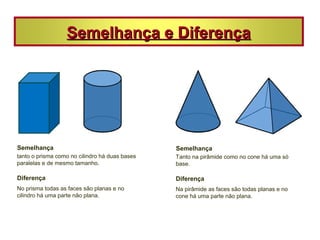
As vistas de um sólido geométrico são representações de acordo com a posição do observador, como superior, inferior, frontal e lateral. Prismas e pirâmides possuem elementos como vértices, arestas e faces, e classificam-se pela forma da base. Poliedros podem ser convexos ou não-convexos e satisfazem a relação de Euler.

1. Vistas
Vistas de um sólido geométrico são suas representações de acordo com a
posição em que o observador o vê: superior, inferior, frontal, lateral, de trás.
Vista superior Vista lateral direita Vista frontal

2. Poliedros – Elementos
Num prisma: Numa pirâmide
existe apenas 1 base
o nº de faces laterais é igual ao nº de lados da base
existem 2 bases
o nº de arestas é o dobro do nº de lados da base
o nº de faces laterais é igual ao nº de lados da base
o nº de vértices é mais 1 que o nº de lados da base
o nº de arestas é o triplo do nº de lados da base
o nº de vértices é igual ao dobro do nº de lados da base

3. Classificação de prismas e pirâmides
Os prismas e as pirâmides classificam-se pelo polígono da base.

4. Poliedros convexos e não-convexos
convexo
Não-convexo

5. Relação de Euler
Se um poliedro é convexo, então vale a relação de Euler (Lê-se Óiler),
ou seja, para um poliedro de V vértices, A arestas e F faces, vale que:
V+F=A+2

6. Semelhança e Diferença
Semelhança Semelhança
tanto o prisma como no cilindro há duas bases Tanto na pirâmide como no cone há uma só
paralelas e de mesmo tamanho. base.
Diferença Diferença
No prisma todas as faces são planas e no Na pirâmide as faces são todas planas e no
cilindro há uma parte não plana. cone há uma parte não plana.

7. Polígonos - Diagonais
n ×( n − 3 ) Onde n é o número de
d= lados
2

8. Simetria
SIMETRIA AXIAL SIMETRIA CENTRAL
ou ou
(simetria de reflexão) (simetria de rotação)
Cada uma das figuras tem um Figuras com simetria central
eixo de simetria

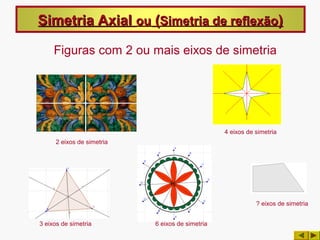
9. Simetria Axial ou (Simetria de reflexão)
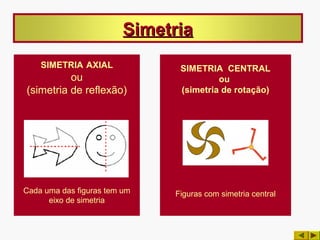
Uma figura tem Simetria axial quando existe pelo menos uma reta que a
divide em duas partes que se podem sobrepor ponto por ponto por
dobragem, isto é por reflexão. A essa reta dá-se o nome de eixo de simetria
O Eixo de Simetria de uma figura é uma
reta r que divide a figura em duas partes
geometricamente iguais.
Para qualquer ponto A numa das partes
existe um ponto A’ na outra parte, tal que:
[AA’] é perpendicular a r .
• Um perfeito exemplo de simetria
encontrada na natureza é o caso da
borboleta Monarca, a qual apresenta um
único eixo de simetria.

10. Simetria Axial ou (Simetria de reflexão)
Figuras com 1 eixo de simetria
Na Natureza Na Arquitetura
(Taj Mahal)
No Desenho Nas letras

11. Simetria Axial ou (Simetria de reflexão)
Figuras com 2 ou mais eixos de simetria
4 eixos de simetria
2 eixos de simetria
? eixos de simetria
3 eixos de simetria 6 eixos de simetria

12. Simetria Central ou (Simetria de rotação)
• Uma figura tem simetria central (de rotação) quando fica invariante por uma
rotação de amplitude inferior a uma volta completa (360°).
• Como a reconhecemos?
Se conseguirmos girar a figura em torno de um ponto fixo, de modo a que
a imagem resultante, através da rotação, coincida com a figura original.
Figuras com simetria Central Figura sem simetria Central
• invariante → é algo que não se altera ao aplicar-se um conjunto de transformações

13. Simetria Central ou (Simetria de rotação)
Simetria central de uma figura
Que simetrias rotacionais tem a figura?
C: Centro da simetria rotacional (ponto em torno C
do qual a figura “roda”)
Ângulo da simetria rotacional: ângulo orientado que descreve o “movimento”
da figura.
3600
900 1800
2700
Meia volta três quartos de uma volta completa
Um quarto de volta
volta