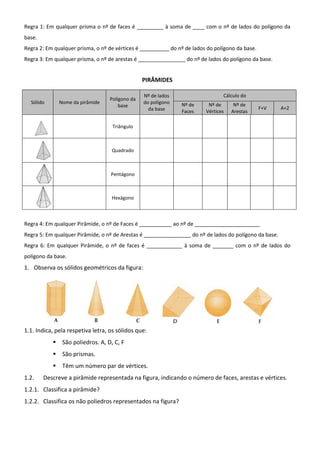
O documento discute os tipos de sólidos geométricos, divididos em poliedros e não poliedros. Poliedros incluem prismas e pirâmides, que são classificados de acordo com o polígono da base. Regras para calcular faces, vértices e arestas de prismas e pirâmides são fornecidas.

1. SÓLIDOS GEOMÉTRICOS (REVISÕES - 5ºano)
Os sólidos geométricos classificam-se em Poliedros e
Não Poliedros.
Os sólidos limitados unicamente por superfícies planas
chamam-se Poliedros.
Os sólidos limitados por porções de superfícies curvas
(em parte ou na totalidade) dizem-se Não Poliedros.
SÃO POLIEDROS: OS PRISMAS E AS PIRÂMIDES.
OS ELEMENTOS DE UM POLIEDRO SÃO AS FACES, AS ARESTAS E OS VÉRTICES.
As faces de um poliedro são polígonos.
Polígonos regulares são polígonos cujos lados são todos iguais.
As pirâmides são poliedros que possuem uma única base e cujas faces laterais são formadas por
triângulos. Numa pirâmide, o número de faces e o número de vértices é igual; Uma pirâmide tem
sempre um número par de arestas.
Os prismas são poliedros que possuem duas bases, que são polígonos iguais. Essas bases são ligadas
por paralelogramos que chamamos faces laterais. Num prisma, o número de arestas é múltiplo de 3.
Os PRISMAS e as PIRÂMIDES classificam-se de acordo com o polígono da base.

2. IGUALDADE DE EULER
Num sólido poliedro verifica-se a seguinte propriedade:
Número de faces + Número de vértices = Número de arestas + 2
NÃO POLIEDROS
EXERCÍCIOS RESOLVIDOS
PRISMAS
Nº de lados do Cálculo do
Polígono da
Sólido Nome do prisma polígono da Nº de Nº de Nº
base F+V A+2
base Faces Vértices Arestas
Triângulo
Quadrado
Rectângulo
Pentágono
Hexágono

3. Regra 1: Em qualquer prisma o nº de faces é _________ à soma de ____ com o nº de lados do polígono da
base.
Regra 2: Em qualquer prisma, o nº de vértices é __________ do nº de lados do polígono da base.
Regra 3: Em qualquer prisma, o nº de arestas é ________________ do nº de lados do polígono da base.
PIRÂMIDES
Nº de lados Cálculo do
Polígono da
Sólido Nome da pirâmide do polígono Nº de Nº de Nº de
base F+V A+2
da base Faces Vértices Arestas
Triângulo
Quadrado
Pentágono
Hexágono
Regra 4: Em qualquer Pirâmide, o nº de Faces é ___________ ao nº de ______________________
Regra 5: Em qualquer Pirâmide, o nº de Arestas é ________________ do nº de lados do polígono da base.
Regra 6: Em qualquer Pirâmide, o nº de faces é ____________ à soma de _______ com o nº de lados do
polígono da base.
1. Observa os sólidos geométricos da figura:
1.1. Indica, pela respetiva letra, os sólidos que:
São poliedros. A, D, C, F
São prismas.
Têm um número par de vértices.
1.2. Descreve a pirâmide representada na figura, indicando o número de faces, arestas e vértices.
1.2.1. Classifica a pirâmide?
1.2.2. Classifica os não poliedros representados na figura?

4. 2. Na figura, está representado um sólido.
Quantos vértices têm o sólido?
Quantas arestas tem o sólido?
Qual das figuras seguintes pode corresponder à planificação do sólido?
Aferição 2011
3. A figura seguinte representa uma pirâmide quadrangular.
Aferição 2011
Na posição em que se encontra a pirâmide, apenas estão visíveis três faces.
Quantas faces da pirâmide não estão visíveis?
4. As pirâmides têm características geométricas que as distinguem dos prismas; por exemplo: O
número de arestas das pirâmides é sempre um múltiplo de 2, enquanto o número de arestas
dos prismas é sempre um múltiplo de 3.
Escreve outra característica geométrica das pirâmides que as distinga dos prismas.
As pirâmides são poliedros que possuem uma única base e cujas faces laterais são formadas por
triângulos.

5. 5. O chão à volta de uma piscina está pavimentado com mosaicos todos iguais, como mostra a
figura.
Aferição 2010
Qual é o nome do polígono representado por cada um dos mosaicos da figura?
Hexágono Pentágono Retângulo Triângulo
6. O sólido representado a seguir tem a forma de um prisma pentagonal.
Quantas arestas tem um prisma pentagonal? 15 arestas
6.1. Qual das figuras seguintes corresponde à planificação de um prisma pentagonal?
Aferição 2010
7. A figura mostra três polígonos que a Maria desenhou, juntando, por um dos seus lados, dois
triângulos retângulos geometricamente iguais.
Aferição 2009
Quais são os nomes dos três polígonos que a Maria desenhou?
□ Losango, Triângulo e Pentágono.

6. x Paralelogramo, Triângulo e Pentágono.
□ Losango, Triângulo e Hexágono.
□ Paralelogramo, Triângulo e Hexágono.
8. O sólido representado na figura faz lembrar uma bola de futebol. Assinala,
com X, o nome dos polígonos das faces deste sólido que estão visíveis na
figura.
Quadriláteros e hexágonos
X Hexágonos e pentágonos Aferição 2008
Pentágonos e triângulos
Triângulos e octógonos
9. Quantos vértices, arestas e faces têm uma pirâmide quadrangular?
Número de vértices: 5
Número de arestas: 8
Número de faces: 5
10. A figura mostra a planificação de um paralelepípedo.
Aferição 2006
10.1. Quantas faces, vértices e arestas tem um paralelepípedo?
Número de faces: 6 faces
Número de arestas: 12 arestas
Número de vértices: 8 vértices