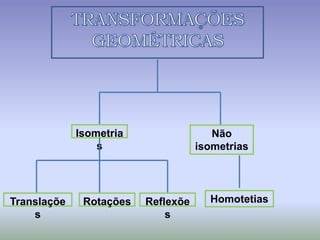
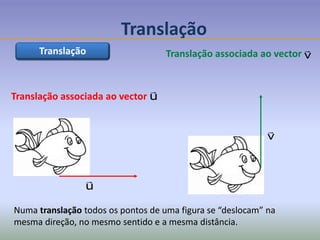
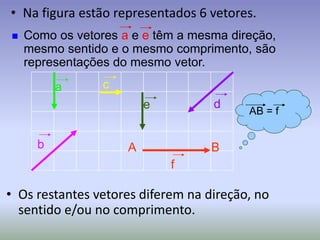
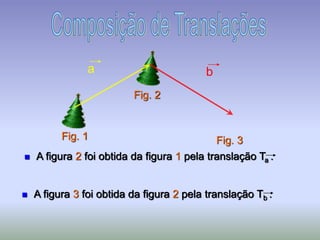
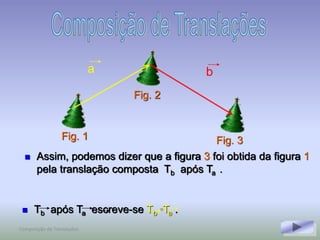
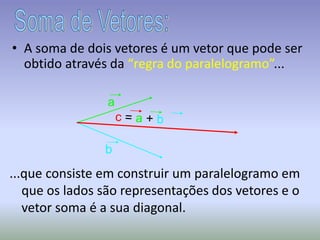
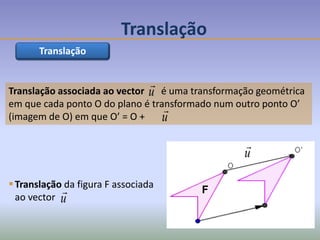
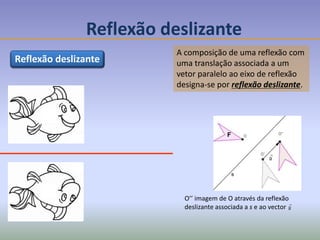
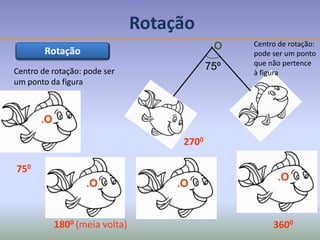
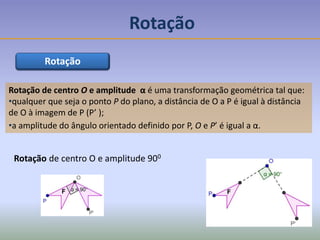
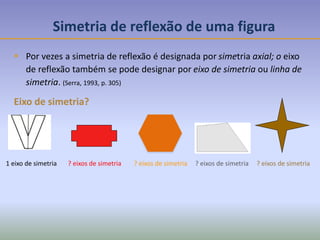
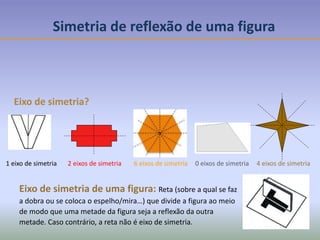
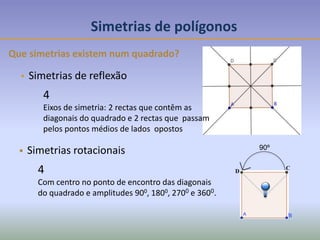
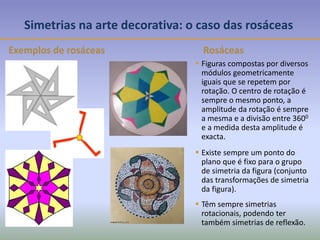
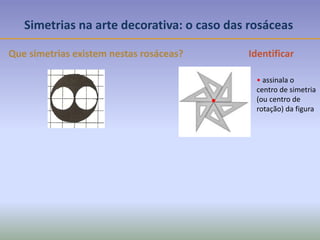
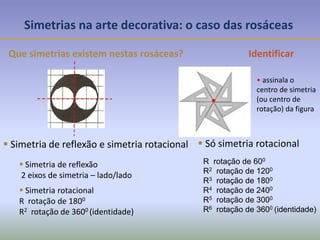
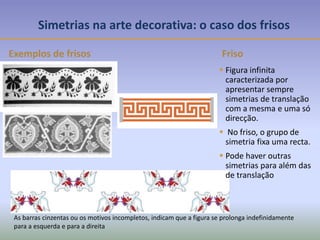
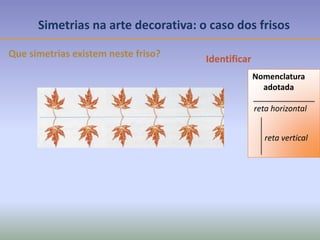
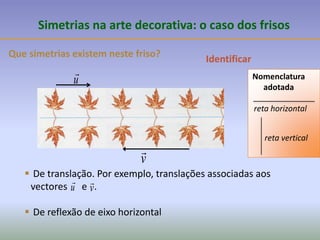
Este documento discute os conceitos de simetria e isometrias em geometria. Resume os quatro tipos fundamentais de isometrias: rotações, translações, reflexões e reflexões deslizantes. Explica como estas transformações geométricas preservam distâncias e como podem ser usadas para analisar a simetria de figuras. Ilustra estes conceitos com exemplos de polígonos, rosáceas e frisos decorativos.

1. ISOMETRIAS
9º ano

2. Simetria: Que significado?
Serão as mãos simétricas?
Será a nossa cara simétrica?
Serão os bonecos simétricos?

3. Simetria: Que significado?
A noção de simetria, sendo essencial em Matemática, não
é exclusiva deste campo
Simetria é uma ideia que o homem tem usado ao longo dos tempos
para tentar compreender e criar ordem, beleza e perfeição. (Serra,
1993, p. 304, cit. Weyl)
A noção de simetria é deveras importante em Matemática, nas
artes visuais e em diversas ciências como a Cristalografia e a
Física. (Oliveira, 1997, p. 70)
Em geometria, simetria define-se em termos de isometrias
Quando a imagem de uma figura, através de uma isometria diferente da
identidade, coincide com a figura original, então a figura tem simetria. (Serra,
1993)

4. Isometria
s
Não
isometrias
Translaçõe
s
Rotações Reflexõe
s
Homotetias

5. Isometria
Definição:
Isometria: Transformação geométrica que preserva as distâncias;
as figuras do plano são transformadas noutras geometricamente
iguais.
 Quatro tipos fundamentais de isometrias:
— Rotação
— Translação
— Reflexão
— Reflexão deslizante

6. Translação
Numa translação todos os pontos de uma figura se “deslocam” na
mesma direção, no mesmo sentido e a mesma distância.
Translação

u

v
Translação associada ao vector

u
Translação associada ao vector

v

7. • Na Fisica as forças representam-se por vetores.
Resistência do ar
Gravidade
• Um vetor é um ser matemático que se define por
uma direção, um sentido e um comprimento.

8. • Uma reta define uma direção e todas as que
lhe são paralelas têm a mesma direção.
Direção horizontal
Direção horizontal
Direção horizontal
Direção vertical Direção vertical

9. • Aqui, a direção horizontal tem ,em A, o
sentido da esquerda para a direita e, em B, o
sentido da direita para a esquerda.
• Para cada direção existem dois sentidos.
A
B

10. • Na figura estão representados 6 vetores.
a
d
c
e
b
f
A B
AB = f
 Como os vetores a e e têm a mesma direção,
mesmo sentido e o mesmo comprimento, são
representações do mesmo vetor.
• Os restantes vetores diferem na direção, no
sentido e/ou no comprimento.

11.  A figura 3 foi obtida da figura 2 pela translação Tb .
Fig. 1
Fig. 2
Fig. 3
a b
 A figura 2 foi obtida da figura 1 pela translação Ta .

12. Composição de Translações
Fig. 1
Fig. 2
Fig. 3
 Assim, podemos dizer que a figura 3 foi obtida da figura 1
pela translação composta Tb após Ta .
 Tb após Ta escreve-se Tb ◦Ta .
a b

13. ...que consiste em construir um paralelogramo em
que os lados são representações dos vetores e o
vetor soma é a sua diagonal.
• A soma de dois vetores é um vetor que pode ser
obtido através da “regra do paralelogramo”...
a
b

14. Translação associada ao vector é uma transformação geométrica
em que cada ponto O do plano é transformado num outro ponto O’
(imagem de O) em que O’ = O +
u

Translação
u

F
Translação da figura F associada
ao vector u

u

Translação

15. Cada ponto de uma figura e a sua imagem estão sobre uma reta
perpendicular ao eixo de reflexão e a igual distância desse eixo.
É como se o peixe e a estrela se estivessem “a ver ao espelho”...
Reflexão Os eixos de reflexão podem, ou não ter pontos em
comum com a(s) figura(s)
eixo de reflexão
Reflexão

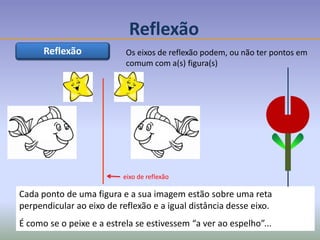
16. Reflexão de eixo s é a transformação geométrica que faz corresponder a
cada ponto O do plano o ponto O’ (imagem de O) de tal modo que:
•a recta s é perpendicular a [O O’] e passa pelo ponto médio de [O O’] (ou
s é a mediatriz de [O O’];
•se O pertence a s, a sua imagem coincide com O.
Reflexão
Reflexão da figura F de de eixo s
s
F
Reflexão

17. Reflexão deslizante
A composição de uma reflexão com
uma translação associada a um
vetor paralelo ao eixo de reflexão
designa-se por reflexão deslizante.
O’’ imagem de O através da reflexão
deslizante associada a s e ao vector
s
u

u

F
Reflexão deslizante

18. Rotação
75º
.ORotação
O peixe da esquerda “rodou” no sentido contrário aos ponteiros do
relógio (sentido positivo), descrevendo um ângulo de vértice O e
amplitude 75 graus.
Rotação de centro O e amplitude 750

19. Rotação
.O
750
.O
3600
O
75º
.
Centro de rotação: pode ser
um ponto da figura
1800 (meia volta)
Centro de rotação:
pode ser um ponto
que não pertence
à figura
.O
.O
2700
Rotação

20. Rotação de centro O e amplitude α é uma transformação geométrica tal que:
•qualquer que seja o ponto P do plano, a distância de O a P é igual à distância
de O à imagem de P (P’ );
•a amplitude do ângulo orientado definido por P, O e P’ é igual a α.
Rotação de centro O e amplitude 900
FF
Rotação
Rotação

21. Retomando a ideia de simetria de uma figura
De entre as aplicações mais interessantes das transformações
e grupos de transformações estão as relacionadas com
questões de simetria. Existindo muitas espécies de simetrias
no plano e no espaço (...). (Oliveira, 1996, p. 187)
— Simetria de reflexão (ou simetria axial)
— Simetria de rotação (ou simetria rotacional)
—Simetria de translação
—Simetria de reflexão deslizante
Há uma simetria para cada um dos quatro tipos de isometrias
referidos. (Serra, 1993, p. 305)

22. Simetria de reflexão de uma figura
Existe, pelo menos, uma reflexão que deixa a figura
globalmente invariante
Como a reconhecemos? Várias hipóteses...
 Se conseguirmos dobrar a figura de tal modo que as
duas partes obtidas se sobreponham exactamente;
 Se conseguirmos colocar um espelho ou mira sobre a
figura de modo a que a junção da parte reflectida com a
não reflectida seja exactamente igual à figura toda;
 Se recortarmos a figura e conseguirmos preencher
exactamente o buraco que fica na folha com a parte
recortada mas virada ao contrário (com a parte de baixo
do papel virada para cima);
 ...

23. Simetria de reflexão de uma figura
 Por vezes a simetria de reflexão é designada por simetria axial; o eixo
de reflexão também se pode designar por eixo de simetria ou linha de
simetria. (Serra, 1993, p. 305)
Eixo de simetria?
1 eixo de simetria ? eixos de simetria ? eixos de simetria? eixos de simetria ? eixos de simetria

24. Simetria de reflexão de uma figura
Eixo de simetria?
1 eixo de simetria 6 eixos de simetria 0 eixos de simetria2 eixos de simetria 4 eixos de simetria
Eixo de simetria de uma figura: Reta (sobre a qual se faz
a dobra ou se coloca o espelho/mira…) que divide a figura ao meio
de modo que uma metade da figura seja a reflexão da outra
metade. Caso contrário, a reta não é eixo de simetria.

25. Figura com simetria rotacional Figura sem simetria rotacional
Simetria rotacional de uma figura
Existe, pelo menos, uma rotação com uma amplitude superior a 00
e inferior a 3600 que deixa a figura globalmente invariante. Só
neste caso se admite também uma simetria rotacional associada a
um ângulo de 3600.
Se conseguirmos girar a figura em torno de um ponto fixo, de modo a que a
imagem resultante, através da rotação, coincida com a figura original.
Como a reconhecemos?
(ou qualquer outro tipo de simetria)

26. Simetria rotacional de uma figura
Que simetrias rotacionais tem a figura?
C: Centro da simetria rotacional (ponto
em torno do qual a figura “roda”)
C
Ângulo da simetria rotacional: ângulo orientado que descreve o
“movimento” da figura.
Três quartos de volta
(270º)
Uma volta inteira
(360º)
Um quarto de volta
(90º)
Meia volta
(180º)

27. Simetria de translação de uma figura
Existe, pelo menos, uma translação que deixa a figura
globalmente invariante
Como a reconhecemos?
Se podemos movimentar a figura segundo uma dada distância e
uma dada direcção (identificadas pelo vector da translação) de
tal modo que o seu transformado coincide com a figura original
Se a figura for infinita, existe essa possibilidade…

28. Simetria de reflexão deslizante de uma figura
Existe, pelo menos, uma reflexão deslizante que deixa a figura
globalmente invariante
Como a reconhecemos?
 Se, por exemplo, depois de desenharmos a figura em papel transparente, de
virarmos o papel ao contrário “em torno” de uma determinada reta e de o
deslocarmos segundo a direção dessa reta, conseguirmos que o transformado
da figura coincida com a figura original.
 Se a figura for infinita, existe essa possibilidade…

29. Simetrias de polígonos
Que simetrias existem num quadrado?
D C
BA

30. 90º
B
C
D
Simetrias de polígonos
Que simetrias existem num quadrado?
 Simetrias de reflexão
 Simetrias rotacionais
4
Com centro no ponto de encontro das diagonais
do quadrado e amplitudes 900, 1800, 2700 e 3600.
4
Eixos de simetria: 2 rectas que contêm as
diagonais do quadrado e 2 rectas que passam
pelos pontos médios de lados opostos

31. Simetrias na arte decorativa: o caso das rosáceas
Exemplos de rosáceas
 Figuras compostas por diversos
módulos geometricamente
iguais que se repetem por
rotação. O centro de rotação é
sempre o mesmo ponto, a
amplitude da rotação é sempre
a mesma e a divisão entre 3600
e a medida desta amplitude é
exacta.
Rosáceas
 Existe sempre um ponto do
plano que é fixo para o grupo
de simetria da figura (conjunto
das transformações de simetria
da figura).
 Têm sempre simetrias
rotacionais, podendo ter
também simetrias de reflexão.

32. Que simetrias existem nestas rosáceas?
Simetrias na arte decorativa: o caso das rosáceas
• assinala o
centro de simetria
(ou centro de
rotação) da figura
•
Identificar

33. Que simetrias existem nestas rosáceas?
Simetrias na arte decorativa: o caso das rosáceas
 Simetria de reflexão
2 eixos de simetria – lado/lado
 Simetria rotacional
R rotação de 1800
R2 rotação de 3600 (identidade)
R rotação de 600
R2 rotação de 1200
R3 rotação de 1800
R4 rotação de 2400
R5 rotação de 3000
R6 rotação de 3600 (identidade)
 Só simetria rotacional
•
 Simetria de reflexão e simetria rotacional
Identificar
• assinala o
centro de simetria
(ou centro de
rotação) da figura

34. Exemplos de frisos
As barras cinzentas ou os motivos incompletos, indicam que a figura se prolonga indefinidamente
para a esquerda e para a direita
 Figura infinita
caracterizada por
apresentar sempre
simetrias de translação
com a mesma e uma só
direcção.
 No friso, o grupo de
simetria fixa uma recta.
 Pode haver outras
simetrias para além das
de translação
Friso
Simetrias na arte decorativa: o caso dos frisos

35. Que simetrias existem neste friso?
Simetrias na arte decorativa: o caso dos frisos
Identificar
reta horizontal
Nomenclatura
adotada
reta vertical

36. Que simetrias existem neste friso?
Simetrias na arte decorativa: o caso dos frisos
u


v
 De translação. Por exemplo, translações associadas aos
vectores e .
 De reflexão de eixo horizontal
Identificar
u


v
reta horizontal
Nomenclatura
adotada
reta vertical

37. Que simetrias existem neste friso?
Simetrias na arte decorativa: o caso dos frisos
Identificar

38. Que simetrias existem neste friso?
Simetrias na arte decorativa: o caso dos frisos
 De reflexão de eixo horizontal
 De reflexão de eixos verticais
 De translação da figura
associadas a vectores com a
direcção de e comprimento
múltiplo do deste vector.
u

Identificar
u

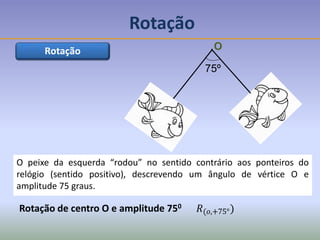
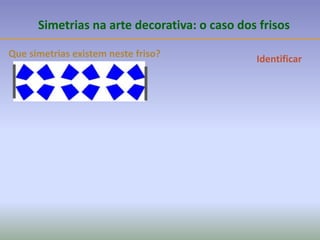
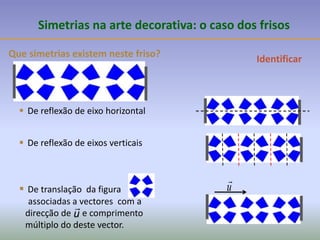
39. A partir de um motivo simples
podem-se construir frisos muito
diversos usando isometrias
Simetrias na arte decorativa: o caso dos frisos
Motivo simples
Construir
[A´, B’, C’, D’] imagem do
motivo simples através de
uma reflexão de eixo r.
A’
B’
C’
D’
[A’´, B’’, C’’, D’’] imagem de
[A´, B’, C’, D’] através de
uma translação de vector
paralelo ao eixo de reflexão
(recta r).
A’
B’
C’
D’
A’’
B’’
C’’
D’’
Nota: O motivo simples é, por vezes, designado por módulo
r