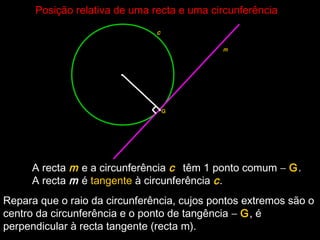
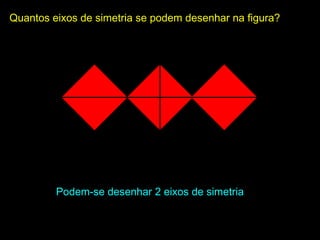
Este documento apresenta conceitos básicos de geometria como retas, segmentos de retas, ângulos, polígonos e circunferências. Define e classifica triângulos, quadriláteros e outros polígonos de acordo com seus lados e ângulos. Explica o que são eixos de simetria e como identificar a posição relativa de uma reta em relação a uma circunferência.

1. GeometriaGeometria

2. Rectas, semi-rectas e segmentos de rectaRectas, semi-rectas e segmentos de recta

3. RETARETA
aa
recta arecta a

4. RETARETA
aa
recta arecta a
AA
BB
ouou
rectarecta
ABAB

5. SEMI-RETASSEMI-RETAS
CC
BB
AA BBAA
CC
ee
AA
Poderemos representar outras semi-rectas, pelasPoderemos representar outras semi-rectas, pelas
suas notações?suas notações?
rr

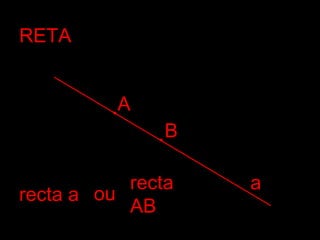
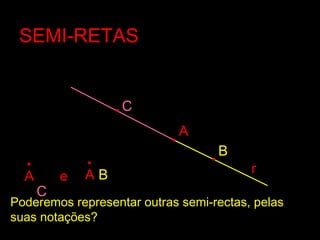
6. SEGMENTOS DE RETASEGMENTOS DE RETA
CC
BB
[A[A B]B][A[A C]C] ee [[CC B]B]
AA
mm

7. ÂNGULOSÂNGULOS
Este ângulo é agudo
A sua amplitude varia entre 0º e 90º
O
P
Q

8. Este ângulo é rectoEste ângulo é recto
A sua amplitude é 90ºA sua amplitude é 90º

9. Este ângulo é obtusoEste ângulo é obtuso
A sua amplitude varia entre 90º e
180º

10. Ângulo rasoÂngulo raso
A
O
B
A sua amplitude é 180ºA sua amplitude é 180º

11. Ângulo giroÂngulo giro
A sua amplitude é 360ºA sua amplitude é 360º

12. POLÍGONOSPOLÍGONOS
• TRIÂNGULOSTRIÂNGULOS
Classificação quanto aos ladosClassificação quanto aos lados

13. TriânguloTriângulo
equiláteroequilátero
Tem 3 ladosTem 3 lados
geometricamentegeometricamente
iguaisiguais

14. TriânguloTriângulo
isóscelesisósceles
Tem 2 lados com o mesmoTem 2 lados com o mesmo
comprimentocomprimento

15. TriânguloTriângulo
escalenoescaleno
Tem 3 lados comTem 3 lados com
comprimentos diferentescomprimentos diferentes

16. Classificação quanto aos ângulosClassificação quanto aos ângulos

17. TriânguloTriângulo
acutânguloacutângulo
Tem 3 ângulos agudosTem 3 ângulos agudos

18. TriânguloTriângulo
rectângulorectângulo
Tem um ângulo rectoTem um ângulo recto

19. TriânguloTriângulo
obtusânguloobtusângulo
Tem um ângulo obtusoTem um ângulo obtuso

20. A soma dos ângulos internos de umA soma dos ângulos internos de um
triângulo é igual a:triângulo é igual a:
180º (180 graus)180º (180 graus)

21. DIAGONAISDIAGONAIS
DiagonalDiagonal é um segmento de rectaé um segmento de recta
que une dois vérticesque une dois vértices opostos,opostos,
não consecutivos de um polígononão consecutivos de um polígono
O triângulo não temO triângulo não tem
diagonaisdiagonais

22. QuadriláterosQuadriláteros
QuadradoQuadrado
• Tem 4 lados com o mesmoTem 4 lados com o mesmo
comprimentocomprimento
• Tem 4 ângulos rectosTem 4 ângulos rectos
• Tem lados opostos paralelosTem lados opostos paralelos
• Tem 2 diagonais perpendiculares eTem 2 diagonais perpendiculares e
comcom o mesmo comprimentoo mesmo comprimento

23. RectânguloRectângulo
•Tem os ladosTem os lados
geometricamente iguaisgeometricamente iguais
dois a doisdois a dois
• Tem 4 ângulos rectosTem 4 ângulos rectos
• Tem lados opostosTem lados opostos
paralelosparalelos
•Tem 2 diagonaisTem 2 diagonais
geometricamente iguaisgeometricamente iguais
não perpendicularesnão perpendiculares

24. ParalelogramoParalelogramo
• Tem lados opostos paralelosTem lados opostos paralelos
•Tem duas diagonais com comprimentosTem duas diagonais com comprimentos
diferentesdiferentes não perpendicularesnão perpendiculares
• Tem ângulos opostos geometricamente iguaisTem ângulos opostos geometricamente iguais

25. LosangoLosango
• 4 lados geometricamente iguais4 lados geometricamente iguais
•2 diagonais perpendiculares com diferentes2 diagonais perpendiculares com diferentes
comprimentoscomprimentos
• Tem lados opostos paralelosTem lados opostos paralelos

26. • TrapéziosTrapézios
TrapézioTrapézio
TrapézioTrapézio
TrapézioTrapézio
isóscelesisósceles
rectângulorectângulo
escalenoescaleno

27. Tem diagonais não perpendicularesTem diagonais não perpendiculares
geometricamente iguaisgeometricamente iguais
Tem 2 diagonais não perpendicularesTem 2 diagonais não perpendiculares
e de diferentes comprimentose de diferentes comprimentos
Tem 2 diagonais não perpendiculares e deTem 2 diagonais não perpendiculares e de
diferentes comprimentosdiferentes comprimentos

28. Outros polígonosOutros polígonos
PentágonoPentágono
HexágonoHexágono
OctógonoOctógono

29. 1ª diagonal1ª diagonal
2ª diagonal2ª diagonal
3ª diagonal3ª diagonal
4ª diagonal4ª diagonal
5ª diagonal5ª diagonal
O pentágono tem 5 diagonaisO pentágono tem 5 diagonais

30. SIMETRIASIMETRIA
O triângulo equilátero tem 3 eixos de simetriaO triângulo equilátero tem 3 eixos de simetria
Quantos eixos de simetria tem o triângulo equilátero?Quantos eixos de simetria tem o triângulo equilátero?

31. O triângulo isósceles tem um eixo de simetriaO triângulo isósceles tem um eixo de simetria
Quantos eixos de simetria tem o triângulo isósceles?Quantos eixos de simetria tem o triângulo isósceles?

32. Quantos eixos de simetria tem o quadrado?Quantos eixos de simetria tem o quadrado?
O quadrado tem 4 eixos de simetriaO quadrado tem 4 eixos de simetria

33. Quantos eixos de simetria tem o rectângulo?Quantos eixos de simetria tem o rectângulo?
O rectângulo tem 2 eixos de simetriaO rectângulo tem 2 eixos de simetria

34. Quantos eixos de simetria tem o pentágono?Quantos eixos de simetria tem o pentágono?
O pentágono regular tem 5O pentágono regular tem 5
eixos de simetriaeixos de simetria
O pentágono não regularO pentágono não regular
tem 1 eixo de simetriatem 1 eixo de simetria

35. Podem-se desenhar 2 eixos de simetriaPodem-se desenhar 2 eixos de simetria
Quantos eixos de simetria se podem desenhar na figura?Quantos eixos de simetria se podem desenhar na figura?

36. Circunferência e Círculo
•
Uma circunferência é uma
linha curva fechada em que todos
os pontos estão à mesma
distância de um outro ponto que
se designa por centro da
circunferência
À circunferência e à
superfície interior à
circunferência damos
o nome de círculo
Centro

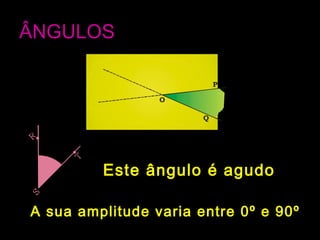
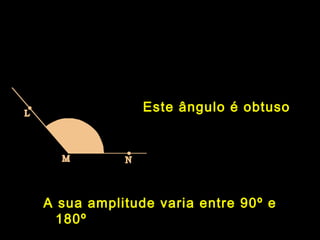
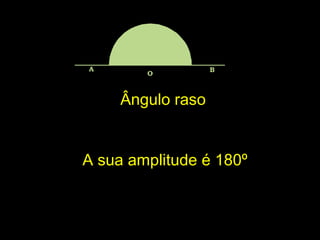
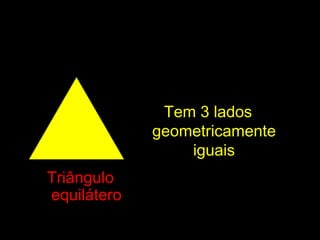
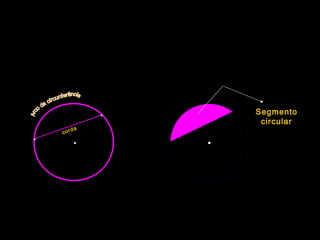
37. CircunferênciaCircunferência
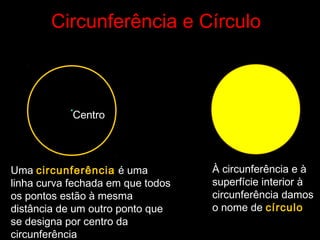
C
O ponto C é o centro da
circunferência r
A
O segmento de recta [CA] é um raio da
circunferência r
B
D
O segmento de recta [BD] é um
diâmetro da circunferência r
E
F
O segmento de recta [EF] é uma
corda da circunferência r
Raio da circunferência – segmento de
recta cujos pontos extremos são o
centro da circunferência e um ponto
qualquer da circunferência
Diâmetro da circunferência - segmento
de recta cujos pontos extremos são dois
pontos da circunferência e contém o seu
centro.
Corda da circunferência - segmento
de recta cujos pontos extremos são
dois pontos da circunferência.
•
•
•
•
•
r

38. •
•
• Segmento
circular
corda

39. •
•
•
Sector circular
raio
raio

40. •
a
b
As circunferências a e b são concêntricas,
isto é, têm o mesmo centro.
Coroa circular

41. Posição relativa de uma recta ePosição relativa de uma recta e
uma circunferênciauma circunferência

42. Posição relativa de uma recta e uma circunferênciaPosição relativa de uma recta e uma circunferência
•
f
g
A recta g e a circunferência f não têm pontos comuns; a
recta g diz-se exterior à circunferência f.

43. Posição relativa de uma recta e uma circunferênciaPosição relativa de uma recta e uma circunferência
•
h
A recta i e a circunferência h têm dois pontos comuns – G
e H; a recta i diz-se secante à circunferência h.
•
•
G
H
i

44. Posição relativa de uma recta e uma circunferênciaPosição relativa de uma recta e uma circunferência
•
c
A recta m e a circunferência c têm 1 ponto comum − G.
A recta m é tangente à circunferência c.
G
m
•
Repara que o raio da circunferência, cujos pontos extremos são o
centro da circunferência e o ponto de tangência − G, é
perpendicular à recta tangente (recta m).