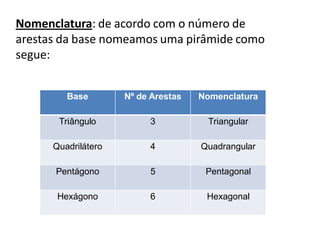
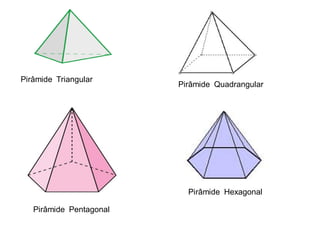
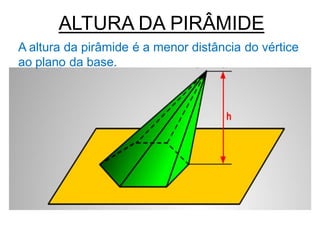
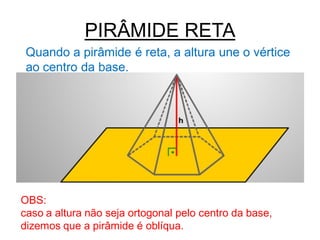
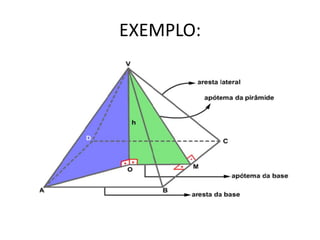
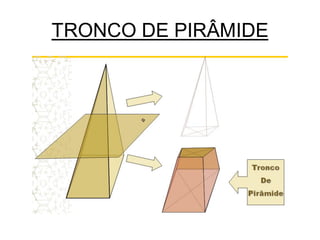
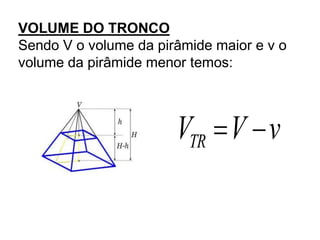
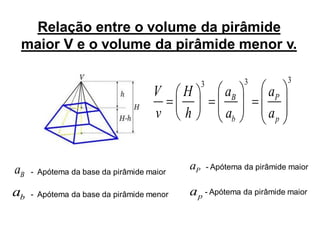
Uma pirâmide é um poliedro com uma base e vértice, onde as faces laterais são triângulos que se encontram no vértice. Existem vários tipos de pirâmides definidas pela forma da base, como triangular, quadrangular ou pentagonal. O documento explica conceitos como altura, apótema, área e volume de pirâmides regulares.

1. PIRÂMIDES
Definição
Uma pirâmide é todo poliedro formado por
uma face inferior e um vértice que une todas
as faces laterais. As faces laterais de uma
pirâmide são regiões triangulares, e o vértice
que une todas as faces laterais é chamado de
vértice da pirâmide.

2. EXEMPLOS DE PIRÂMIDE

3. Nomenclatura: de acordo com o número de
arestas da base nomeamos uma pirâmide como
segue:
Base Nº de Arestas Nomenclatura
Triângulo 3 Triangular
Quadrilátero 4 Quadrangular
Pentágono 5 Pentagonal
Hexágono 6 Hexagonal

4. Pirâmide Triangular
Pirâmide Quadrangular
Pirâmide Hexagonal
Pirâmide Pentagonal

5. ALTURA DA PIRÂMIDE
A altura da pirâmide é a menor distância do vértice
ao plano da base.

6. PIRÂMIDE RETA
Quando a pirâmide é reta, a altura une o vértice
ao centro da base.
OBS:
caso a altura não seja ortogonal pelo centro da base,
dizemos que a pirâmide é oblíqua.

7. PIRÂMIDE REGULAR
Definição
Pirâmide regular é uma pirâmide reta cuja
base é um polígono regular.
OBS: numa pirâmide regular, as faces
laterais são triângulos isósceles
congruentes.

8. APÓTEMA DA PIRÂMIDE
Definição
Denominamos apótema de uma pirâmide
regular, a altura do triângulo isósceles da
face lateral.

9. EXEMPLO:

10. Relação entre a altura da prâmide (h), o
apótema da base ab e o apótema da
pirâmide a p .
2 2 2
ap ab h

11. Exemplo:
1) Uma pirâmide quadrangular regular tem 4m
de altura e a aresta da base mede 6m. Calcule
seu o aótema da base e do apótema da
pirâmide.
ab = 3
2 2 2
ap ab h
2 2
g 3 4 9 16 5m

12. ÁREA
A área total AT de uma pirâmide é a
soma da área da superfície lateral AS L com
a área da base AB .
AT ASL AB

13. VOLUME
O volume de uma pirâmide é sempre o
produto da área da base vezes a altura,
dividido por três.
AB . h
V
3

14. EXEMPLOS
2)Uma pirâmide quadrangular regular tem 4m
de altura e a aresta da base mede 6m. Calcule
seu volume e a área total.
Solução. Observando os elementos na
figura, temos:
i) Volume:
2
AB .h 6 .4 (36).4 3
V pirâmide (12).(4) 48m
3 3 3
ii) Área total:
g 32 42 9 16 5m
AB (6)2 36m2
(6).(5) At Ab Al 36 60 96m2
AS L 4. 4 15 60m2
2

15. 3) Calcular a área da base, área lateral, área total e o volume da pirâmide
quadrangular regular de apótema 5cm e apótema da base 2cm.
Solução. Se o apótema da base mede 2cm, então a aresta da
base mede 4cm. Observando os elementos na figura, temos:
i) Áreas:
h 52 22 21cm
AB (4)2 16cm2
(4).(5) AT AB AS L 16 40 56cm2
AS L 4. 4 10 40cm2
2
ii) Volume:
AB .h 16 .( 21) 16 21
V cm3
3 3 3

16. 4) Calcule o volume de uma pirâmide hexagonal regular de área da
base 288 3 m2 e apótema 13m.
Solução. A área da base é o sêxtuplo da área de
um triângulo equilátero com lado de mesma
medida da aresta do hexágono. Temos:
l2 3
Ab 6. l2 3 (4).( 288 )
4 6. 288 3 l2 l 192 8 3m
4 6
Ab 288 3
O apótema do hexágono é a altura do triângulo equilátero. A
altura da pirâmide é calculada com a relação de Pitágoras no
triângulo retângulo de hipotenusa 13m.
l 3 8 3 3 (8)(3)
ap 12 m Ab .h 288 3 .(5)
2 2 2 V 96 3 .(5) 480 3m 3
3 3
h 13 2 12 2 169 144 25 5m

17. TRONCO DE PIRÂMIDE

18. VOLUME DO TRONCO
Sendo V o volume da pirâmide maior e v o
volume da pirâmide menor temos:
VTR V v

19. Relação entre o volume da pirâmide
maior V e o volume da pirâmide menor v.
3 3 3
V H aB aP
v h ab ap
aB - Apótema da base da pirâmide maior
aP - Apótema da pirâmide maior
ab - Apótema da base da pirâmide menor a p - Apótema da pirâmide maior