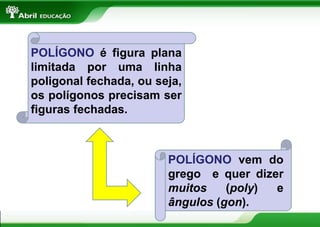
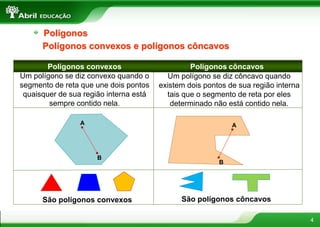
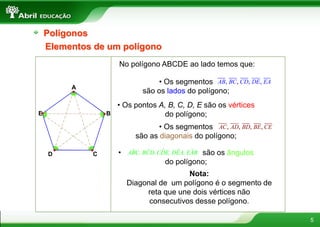
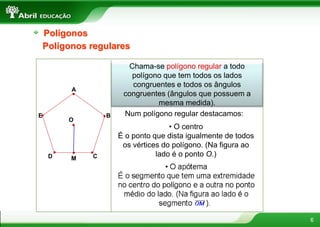
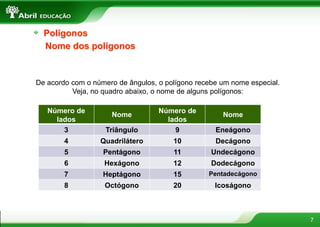
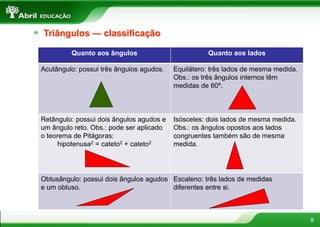
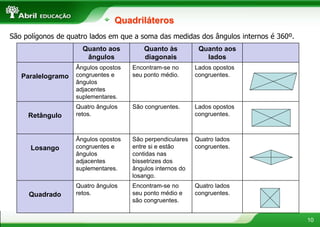
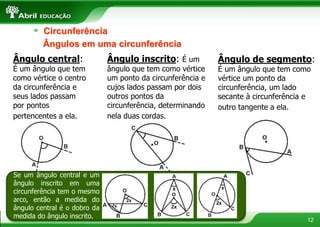
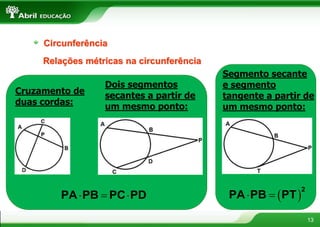
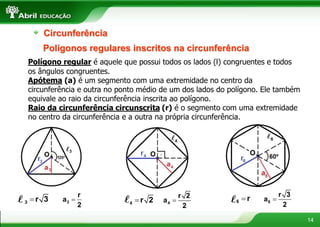
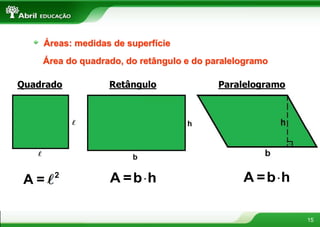
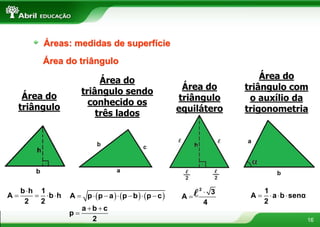
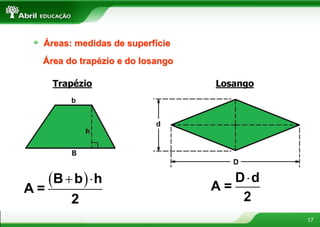
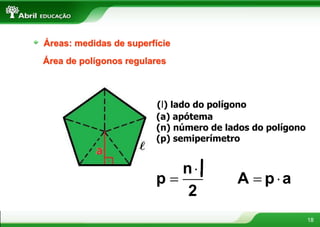
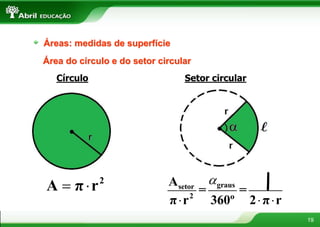
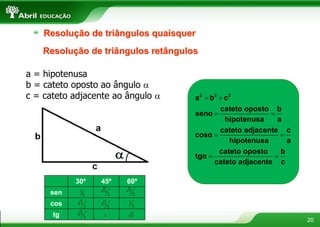
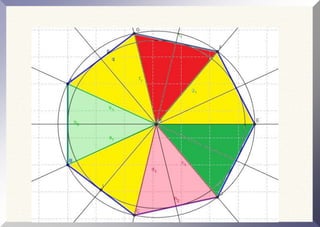
O documento aborda conceitos fundamentais sobre polígonos, incluindo definição, classificação, e propriedades, com exemplos de polígonos regulares e suas características. São apresentados tópicos como a soma dos ângulos internos e externos, as diferentes formas de triângulos e quadriláteros, além de explicações sobre circunferências e medidas de superfície. O material também inclui fórmulas para cálculo de áreas e relações métricas em triângulos e polígonos.

1. Aula de Matemática
Professor : Neilton Satel
02 de setembro 2014
Bom dia!

2. POLÍGONO vem do
grego e quer dizer
muitos (poly) e
ângulos (gon).
POLÍGONO é figura plana
limitada por uma linha
poligonal fechada, ou seja,
os polígonos precisam ser
figuras fechadas.

3. 3
Polígonos
Definição
Chama-se polígono toda linha poligonal fechada simples
juntamente com os pontos da região interna que essa linha
determina.
As figuras a seguir são polígonos
As figuras a seguir não são polígonos

4. 4
Um polígono se diz convexo quando o
segmento de reta que une dois pontos
quaisquer de sua região interna está
sempre contido nela.
Polígonos convexos e polígonos côncavos
Polígonos convexos Polígonos côncavos
Um polígono se diz côncavo quando
existem dois pontos de sua região interna
tais que o segmento de reta por eles
determinado não está contido nela.
A
B
A
B
São polígonos convexos São polígonos côncavos
Polígonos

5. 5
Polígonos
Elementos de um polígono
No polígono ABCDE ao lado temos que:
A
B
C
D
E
• Os segmentos
são os lados do polígono;
, , , ,
AB BC CD DE EA
• Os pontos A, B, C, D, E são os vértices
do polígono;
• Os segmentos
são as diagonais do polígono;
, , , ,
AC AD BD BE CE
• são os ângulos
do polígono;
ˆ ˆ
ˆ ˆ ˆ
ABC, BCD, CDE, DEA, EAB
Nota:
Diagonal de um polígono é o segmento de
reta que une dois vértices não
consecutivos desse polígono.

6. 6
Polígonos
Chama-se polígono regular a todo
polígono que tem todos os lados
congruentes e todos os ângulos
congruentes (ângulos que possuem a
mesma medida).
Polígonos regulares
A
B
C
D
E Num polígono regular destacamos:
• O centro
É o ponto que dista igualmente de todos
os vértices do polígono. (Na figura ao
lado é o ponto O.)
M
O

7. 7
Nome dos polígonos
De acordo com o número de ângulos, o polígono recebe um nome especial.
Veja, no quadro abaixo, o nome de alguns polígonos:
Número de
lados
Nome
Número de
lados
Nome
3 Triângulo 9 Eneágono
4 Quadrilátero 10 Decágono
5 Pentágono 11 Undecágono
6 Hexágono 12 Dodecágono
7 Heptágono 15 Pentadecágono
8 Octógono 20 Icoságono
Polígonos

8. 8
Polígonos
Soma das medidas dos
ângulos internos:
 
180º 2
i
S n
 
Soma das medidas dos
ângulos externos:
360º
e
S 
Ângulos internos de um
polígono regular:
 
180º 2
ou
i
i i
n
S
a a
n n

 
Ângulos externos de
um polígono regular:
360º
ou
e
e e
S
a a
n n
 
Número de diagonais
de um polígono:
 
3
2
n n
d



9. 9
Triângulos ― classificação
Quanto aos ângulos Quanto aos lados
Acutângulo: possui três ângulos agudos. Equilátero: três lados de mesma medida.
Obs.: os três ângulos internos têm
medidas de 60º.
Retângulo: possui dois ângulos agudos e
um ângulo reto. Obs.: pode ser aplicado
o teorema de Pitágoras:
hipotenusa2 = cateto2 + cateto2
Isósceles: dois lados de mesma medida.
Obs.: os ângulos opostos aos lados
congruentes também são de mesma
medida.
Obtusângulo: possui dois ângulos agudos
e um obtuso.
Escaleno: três lados de medidas
diferentes entre si.

10. 10
Quadriláteros
Quanto aos
ângulos
Quanto às
diagonais
Quanto aos
lados
Paralelogramo
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
Encontram-se no
seu ponto médio.
Lados opostos
congruentes.
Retângulo
Quatro ângulos
retos.
São congruentes. Lados opostos
congruentes.
Losango
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
São perpendiculares
entre si e estão
contidas nas
bissetrizes dos
ângulos internos do
losango.
Quatro lados
congruentes.
Quadrado
Quatro ângulos
retos.
Encontram-se no
seu ponto médio e
são congruentes.
Quatro lados
congruentes.
São polígonos de quatro lados em que a soma das medidas dos ângulos internos é 360º.

11. 11
Quadriláteros
Os trapézios são quadriláteros que têm apenas um par de lados
paralelos, chamados base maior e base menor.
Trapézio retângulo
É todo trapézio que tem dois
ângulos retos. Nele, um dos
lados que não é base é
perpendicular às duas bases.
Trapézio isósceles
É todo trapézio que tem dois
lados não paralelos
congruentes.

12. 12
Circunferência
Ângulos em uma circunferência
Ângulo central:
É um ângulo que tem
como vértice o centro
da circunferência e
seus lados passam
por pontos
pertencentes a ela.
Ângulo inscrito: É um
ângulo que tem como vértice
um ponto da circunferência e
cujos lados passam por dois
outros pontos da
circunferência, determinando
nela duas cordas.
Ângulo de segmento:
É um ângulo que tem como
vértice um ponto da
circunferência, um lado
secante à circunferência e
outro tangente a ela.
Se um ângulo central e um
ângulo inscrito em uma
circunferência tem o mesmo
arco, então a medida do
ângulo central é o dobro da
medida do ângulo inscrito.

13. 13
Circunferência
Relações métricas na circunferência
Cruzamento de
duas cordas:
Dois segmentos
secantes a partir de
um mesmo ponto:
  
PA PB PC PD
Segmento secante
e segmento
tangente a partir de
um mesmo ponto:
 
 
2
PA PB PT

14. 14
Circunferência
Polígonos regulares inscritos na circunferência
Polígono regular é aquele que possui todos os lados (l) congruentes e todos
os ângulos congruentes.
Apótema (a) é um segmento com uma extremidade no centro da
circunferência e outra no ponto médio de um dos lados do polígono. Ele também
equivale ao raio da circunferência inscrita ao polígono.
Raio da circunferência circunscrita (r) é o segmento com uma extremidade
no centro da circunferência e a outra na própria circunferência.

3
r
a
2

4
r 2
a
2

6
r 3
a
2

3 r 3
l 
4 r 2
l 
6 r
l

15. 15
Áreas: medidas de superfície
Área do quadrado, do retângulo e do paralelogramo
Quadrado Retângulo Paralelogramo

A =b h 
A =b h
2
A = l

16. 16
Áreas: medidas de superfície
Área do triângulo
Área do
triângulo
Área do
triângulo sendo
conhecido os
três lados
Área do
triângulo
equilátero
Área do
triângulo com
o auxílio da
trigonometria

   
b h 1
A b h
2 2
     
      
 

A p p a p b p c
a b c
p
2
   
1
A a b senα
2


2
3
A
4
l

17. 17
Áreas: medidas de superfície
Área do trapézio e do losango
Trapézio Losango
 
 
B b h
A =
2

D d
A =
2

18. 18
Áreas: medidas de superfície
Área de polígonos regulares
(l) lado do polígono
(a) apótema
(n) número de lados do polígono
(p) semiperímetro
 
A p a
.


n
p
2
l

19. 19
Áreas: medidas de superfície
Área do círculo e do setor circular
Círculo Setor circular
  2
A π r 
  
graus
setor
2
A
= =
π r 360º 2 π r
l

20. 20
Resolução de triângulos quaisquer
Resolução de triângulos retângulos
 
 
 
 
2 2 2
a b c
cateto oposto b
senα
hipotenusa a
cateto adjacente c
cosα
hipotenusa a
cateto oposto b
tgα
cateto adjacente c
a = hipotenusa
b = cateto oposto ao ângulo 
c = cateto adjacente ao ângulo 
30º 45º 60º
sen
cos
tg
1
2
1
2
2
2
2
2
3
2
3
2
3
3 3
1