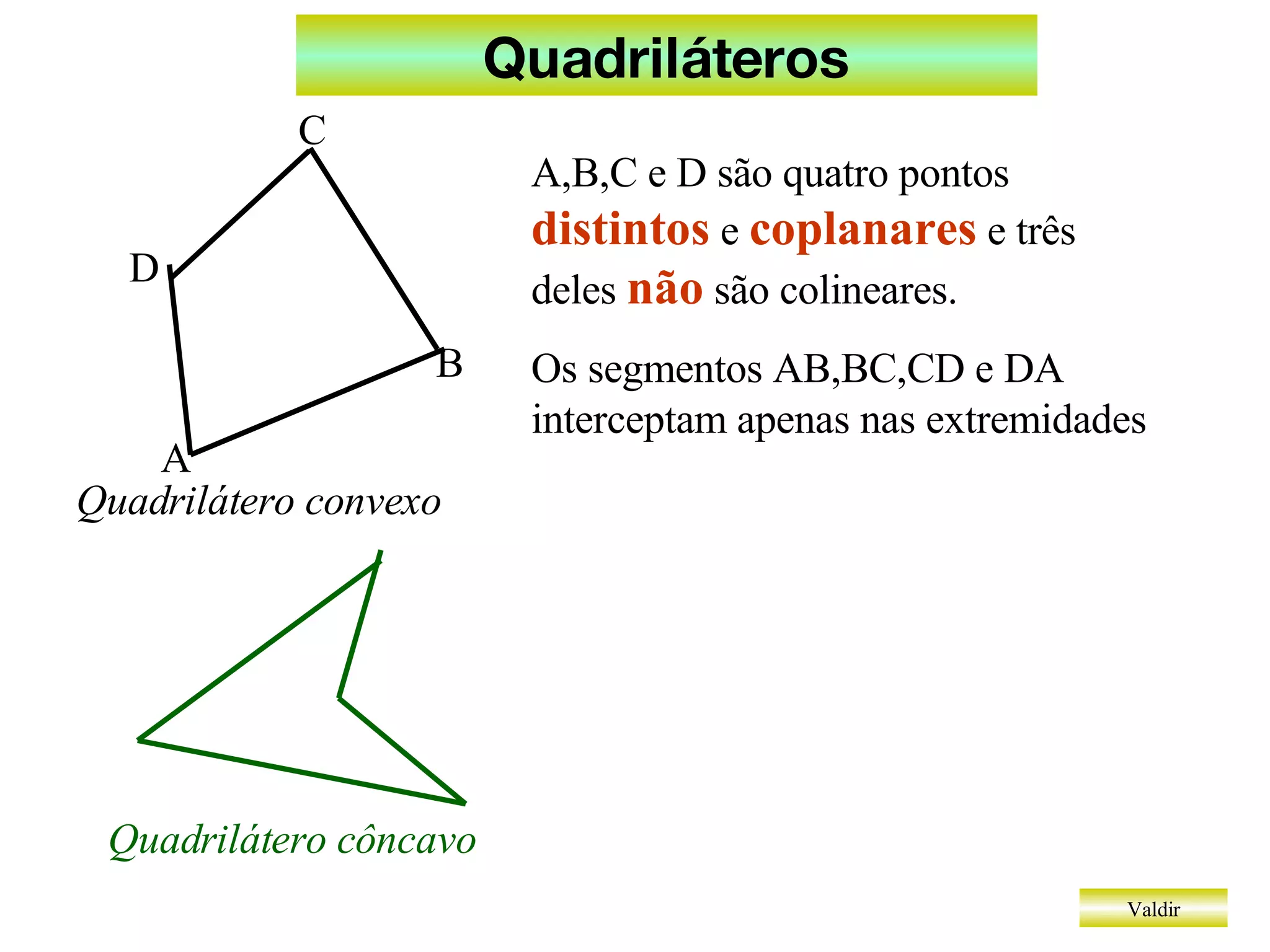
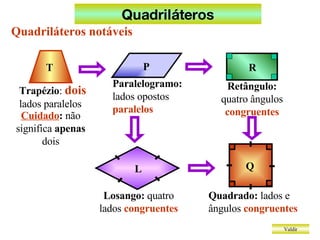
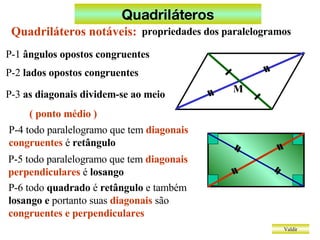
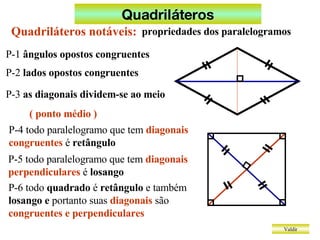
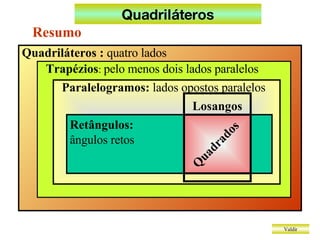
O documento discute diferentes tipos de quadriláteros, incluindo trapézios, paralelogramos, retângulos, losangos e quadrados. Ele lista as propriedades definidoras de cada um, como dois lados paralelos para trapézios, lados opostos paralelos para paralelogramos, e todos os ângulos retos para retângulos.

1. Quadriláteros Valdir A,B,C e D são quatro pontos distintos e coplanares e três deles não são colineares. Os segmentos AB,BC,CD e DA interceptam apenas nas extremidades Quadrilátero convexo Quadrilátero côncavo A B C D

2. Quadriláteros Valdir Quadriláteros notáveis Trapézio : dois lados paralelos Cuidado : não significa apenas dois Paralelogramo: lados opostos paralelos Retângulo: quatro ângulos congruentes Losango: quatro lados congruentes Quadrado: lados e ângulos congruentes T P R L Q

3. Quadriláteros Valdir  +  = 180° Quadriláteros notáveis: propriedades dos paralelogramos P-1 ângulos opostos congruentes P-2 lados opostos congruentes P-3 as diagonais dividem-se ao meio ( ponto médio ) P-4 todo paralelogramo que tem diagonais congruentes é retângulo P-5 todo paralelogramo que tem diagonais perpendiculares é losango P-6 todo quadrado é retângulo e também losango e portanto suas diagonais são congruentes e perpendiculares     

4. Quadriláteros Valdir P-1 ângulos opostos congruentes P-2 lados opostos congruentes P-3 as diagonais dividem-se ao meio ( ponto médio ) P-4 todo paralelogramo que tem diagonais congruentes é retângulo P-5 todo paralelogramo que tem diagonais perpendiculares é losango P-6 todo quadrado é retângulo e também losango e portanto suas diagonais são congruentes e perpendiculares Quadriláteros notáveis: propriedades dos paralelogramos M

5. Quadriláteros Valdir P-1 ângulos opostos congruentes P-2 lados opostos congruentes P-3 as diagonais dividem-se ao meio ( ponto médio ) P-4 todo paralelogramo que tem diagonais congruentes é retângulo P-5 todo paralelogramo que tem diagonais perpendiculares é losango P-6 todo quadrado é retângulo e também losango e portanto suas diagonais são congruentes e perpendiculares Quadriláteros notáveis: propriedades dos paralelogramos

6. Quadriláteros Valdir Resumo Quadriláteros : quatro lados Losangos Quadrados Trapézios : pelo menos dois lados paralelos Paralelogramos: lados opostos paralelos Retângulos: ângulos retos