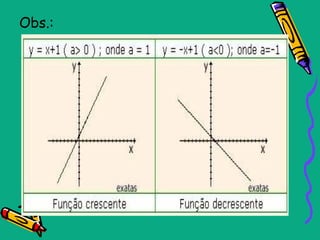
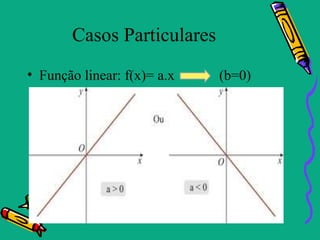
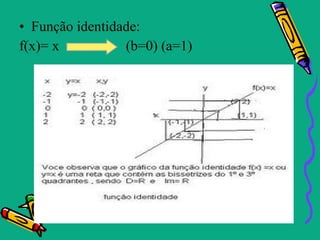
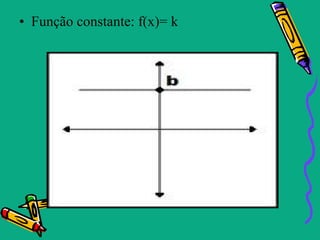
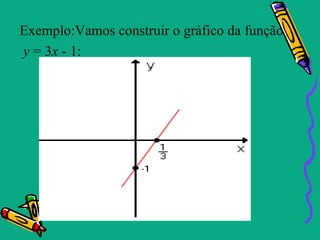
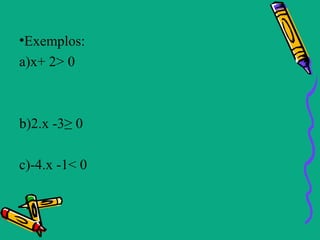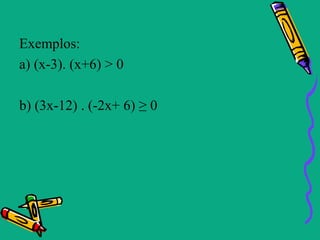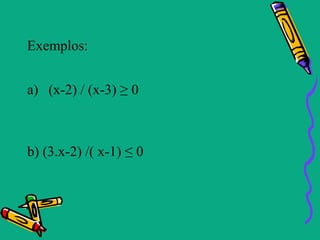Este documento descreve as funções polinomiais do 1o grau, também chamadas de funções afins. Elas são definidas por uma equação da forma f(x)=ax + b, onde a e b são números reais e a ≠ 0. O gráfico de uma função afim é uma reta. O documento também aborda conceitos como coeficientes angular e linear, zeros da função, inequações do 1o grau e casos particulares como função linear, identidade e constante.

1. Função Polinomial do 1º grau
Marcela Monteiro

2. História
•O conceito de função é um dos mais
importantes da Matemática. Este conceito
sofreu uma grande evolução ao longo dos
séculos, sendo que a introdução do método
analítico na definição de função (séc., XVI,
séc. XVII) veio revolucionar a Matemática.

3. •Desde o tempo dos Gregos até à Idade Moderna a
teoria dominante era a Geometria Euclidiana que tinha
como elementos base o ponto, a reta e o plano.
•Vai ser a partir desta época que uma nova teoria, o
Cálculo Infinitesimal, vai surgir e que se acaba por
revelar capital no desenvolvimento da Matemática
contemporânea. A noção de função vai ser um dos
fundamentos do Cálculo Infinitesimal.

4. • Foi Leibniz (1646 - 1716) quem primeiro usou o
termo "função" em 1673 no manuscrito Latino
"Methodus tangentium inversa, seu de fuctionibus".
•Um retoque final nesta definição viria a ser dado em
1748 por Euler (1707 - 1783) - um antigo aluno de
Bernoulli - substituindo o termo "quantidade" por
"expressão analítica". Foi também Euler quem
introduziu a notação f(x).

5. Função Polinomial do 1º grau
Chama-se função polinomial do 1º grau, ou
função afim,a qualquer função de IR em
IR dada por uma lei da forma f(x)=a.x+b,onde a e
b são números reais dados e
a 0.

6. Na função f(x) = a.x + b, o número a é chamado
de coeficiente angular e o número b é chamado
coeficiente linear.
Veja alguns exemplos de funções polinomiais do
1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0

7. Obs.:

8. Casos Particulares
• Função linear: f(x)= a.x (b=0)

9. • Função identidade:
f(x)= x (b=0) (a=1)

10. • Função constante: f(x)= k

11. Gráfico
O gráfico de uma função polinomial do 1º
grau, y = a.x + b, com a0, é uma reta oblíqua
aos eixos Ox e Oy.

12. Exemplo:Vamos construir o gráfico da função
y = 3x - 1:

13. Zero da função do 1º grau
Chama-se zero ou raiz da função polinomial
do 1º grau f(x) = a.x + b, a ≠ 0, o número real
x tal que f(x) = 0.
Temos:
f(x) = 0 a.x + b = 0 x= -b/ a

14. • Exemplos:
a) f(x) = 2x - 5:
b) g(x) = 3x + 6:
c) Cálculo da abscissa do ponto em que o gráfico
de h(x) = -2x + 10 corta o eixo das abscissas:

15. Inequações do 1 grau: o
Define-se inequação do 1o grau na variável x
como sendo toda desigualdade que pode ser
reduzida a uma das formas: a.x+b≥ 0, a.x+b≤
0, a.x+b> 0 ou a.x+> 0, a, b reais e a não
nulo.

16. •Exemplos:
a)x+ 2> 0
b)2.x -3≥ 0
c)-4.x -1< 0

17. •Inequações Produto do 1o grau:
Dadas as funções f (x) e g (x) afins, chamamos
de inequação produto a toda inequação que pode
assumir uma das seguintes formas:
f(x).g(x) ≥ 0, f(x). g(x)≤ 0, f(x).g(x)> 0 ou
f(x).g(x)> 0,
Obs.: A solução será através do quadro de sinais
que se obtém a partir do estudo de sinais de cada
função.

18. Exemplos:
a) (x-3). (x+6) > 0
b) (3x-12) . (-2x+ 6) ≥ 0

19. Inequações Quociente do 1o grau:
Dadas as funções f (x) e g (x) afins, chamamos
de inequação produto a toda inequação que pode
assumir uma das seguintes formas:
f(x)/g(x) ≥ 0, f(x)/g(x)≤ 0, f(x)/g(x)> 0 ou
f(x)/g(x)> 0
Obs.: A solução é análoga ao de inequações
produto

20. Exemplos:
a) (x-2) / (x-3) ≥ 0
b) (3.x-2) /( x-1) ≤ 0

21. "A mudança deve acontecer de dentro
para fora. Os seus pensamentos
determinarão diretamente a forma que
você vê o mundo. Pense positivo! Pense
que você pode e que você é capaz de
coisas maiores." (Dr. Jô Furlan)