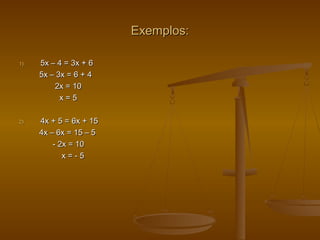Este documento discute funções polinomiais do primeiro grau. Explica que estas funções são equações com variáveis de expoente um, e que seus gráficos formam uma reta. Apresenta exemplos de problemas envolvendo funções lineares e como representá-los graficamente.

1. FUNÇÃO POLINOMIAL DO 1º GRAUFUNÇÃO POLINOMIAL DO 1º GRAU
Aluna: Renata Dias Melo VarellaAluna: Renata Dias Melo Varella
Professora: NilceProfessora: Nilce

2. Idéia Inicial:Idéia Inicial:
 Equações = sentenças matemáticas abertas, expressas por uma igualdade.Equações = sentenças matemáticas abertas, expressas por uma igualdade.
Ex.: x + 5 = 4Ex.: x + 5 = 4
aberta Igualdade
Quando a sentença matemática é fechada, podemos
afirmar quando é falsa ou verdadeira.
Ex.: 5 – 8 = 4 (F) 16 + 5 = 21 (V)

3. DefiniçãoDefinição
 É a igualdade entre duas expressões numéricas, com expoente da variávelÉ a igualdade entre duas expressões numéricas, com expoente da variável
igual a um.igual a um.
Ex.: x + 4 = 3x + 8 ou y – 1 = 5Ex.: x + 4 = 3x + 8 ou y – 1 = 5
 As variáveis são chamadas, também, de incógnitas.As variáveis são chamadas, também, de incógnitas.
 As expressões numéricas separadas pelo sinal de igualdade (=) chamam-As expressões numéricas separadas pelo sinal de igualdade (=) chamam-
se de membros, e cada membro é composto de termos. Em um termo, ose de membros, e cada membro é composto de termos. Em um termo, o
fator numérico que acompanha a variável é chamado de coeficiente.fator numérico que acompanha a variável é chamado de coeficiente.
Ex.: 3x – 2 = x + 8Ex.: 3x – 2 = x + 8
1º membro 2º membro

4. Exemplos:Exemplos:
1)1) 5x – 4 = 3x + 65x – 4 = 3x + 6
5x – 3x = 6 + 45x – 3x = 6 + 4
2x = 102x = 10
x = 5x = 5
2)2) 4x + 5 = 6x + 154x + 5 = 6x + 15
4x – 6x = 15 – 54x – 6x = 15 – 5
- 2x = 10- 2x = 10
x = - 5x = - 5

5. GRÁFICOS DE UMA FUNÇÃO DO 1º GRAUGRÁFICOS DE UMA FUNÇÃO DO 1º GRAU
 Função AfimFunção Afim
Dados a e b, sendo números reais quaisquer, denominando-se aDados a e b, sendo números reais quaisquer, denominando-se a ≠ 0, chama-se≠ 0, chama-se
de função afim uma função que está com a seguinte definição:de função afim uma função que está com a seguinte definição:
f(x) = ax + b, sendo todo número realf(x) = ax + b, sendo todo número real
O gráfico da função afim corta o eixo y nos pontos (0, b) e o gráfico é uma reta.O gráfico da função afim corta o eixo y nos pontos (0, b) e o gráfico é uma reta.
Ex.: F(x) = 2 x + 1Ex.: F(x) = 2 x + 1
xx F(x)F(x)
-2-2 -3-3
-1-1 -1-1
00 11
11 33 -1-2 0
1
1
-1
-3
3
x
y

6. GRÁFICOS DE UMA FUNÇÃO DO 1º GRAUGRÁFICOS DE UMA FUNÇÃO DO 1º GRAU
 Existem outros tipos de funções para obtenção de gráficos, como:Existem outros tipos de funções para obtenção de gráficos, como:
- função linear ( b= 0) e é escrita na forma f(x) = ax- função linear ( b= 0) e é escrita na forma f(x) = ax
- função identidade (a = 1 e b = 0) e escrita na forma f(x) = x- função identidade (a = 1 e b = 0) e escrita na forma f(x) = x
- função constante (a = o) e escrita na forma f(x) = c- função constante (a = o) e escrita na forma f(x) = c

7. PROBLEMA ENVOLVENDO A FUNÇÃO DE 1ºPROBLEMA ENVOLVENDO A FUNÇÃO DE 1º
GRAUGRAU
Situação envolvendo Função Linear:Situação envolvendo Função Linear:
No mês de Janeiro Claudia precisou comprar alguns livros escolares para seuNo mês de Janeiro Claudia precisou comprar alguns livros escolares para seu
filho, e na época custavam R$ 40,00 cada um. Desta forma, podemosfilho, e na época custavam R$ 40,00 cada um. Desta forma, podemos
elaborar a seguinte tabela (referente a compra de 05 livros) e escrever daelaborar a seguinte tabela (referente a compra de 05 livros) e escrever da
forma:forma:
Quantidade de livrosQuantidade de livros Preço a pagar em R$Preço a pagar em R$
11 40,0040,00
22 80,0080,00
33 120,00120,00
44 160,00160,00
55 200,00200,00
Preço a pagar = 40,00 (quantidade de livros)
Então, podemos dizer:
F(x) = 40,00 . X ou y = 40,00 x

8. REFERÊNCIA BIBLIOGRÁFICAREFERÊNCIA BIBLIOGRÁFICA
CASTRO, Luiz Roberto da Silveira; DOLCE, Osvaldo; GOULART, MárcioCASTRO, Luiz Roberto da Silveira; DOLCE, Osvaldo; GOULART, Márcio
Cintra; IEZZI, Gelson; MACHADO, Antonio dos Santos; MACHADO, NilsonCintra; IEZZI, Gelson; MACHADO, Antonio dos Santos; MACHADO, Nilson
José; TEIXEIRA, José Carlos.José; TEIXEIRA, José Carlos. Matemática.Matemática. São Paulo: Atual EditoraSão Paulo: Atual Editora
LTDA, 1992. p. 78-91.LTDA, 1992. p. 78-91.