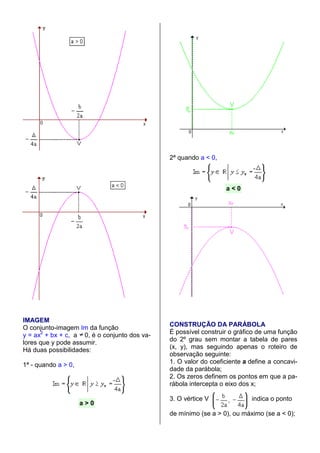
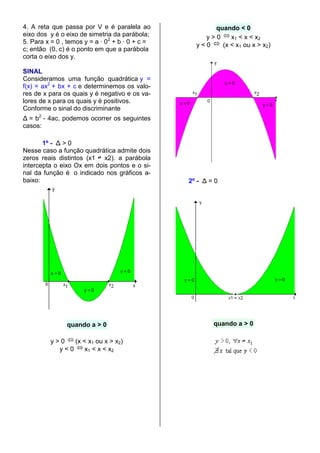
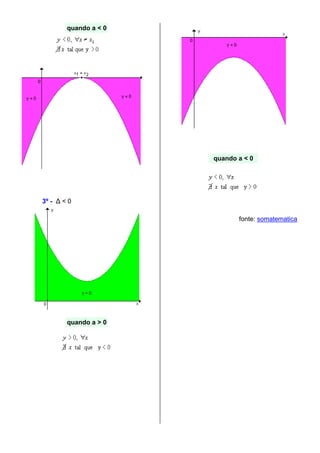
1) Uma função quadrática é definida como f(x) = ax2 + bx + c, onde a, b e c são números reais e a ≠ 0. O gráfico de uma função quadrática é uma parábola. 2) O sinal de a determina a concavidade da parábola, enquanto os zeros da função determinam os pontos onde a parábola intercepta o eixo x. 3) O vértice da parábola tem coordenadas (-b/2a, f(-b/2a)) e indica o ponto de mínimo ou máximo

1. Função Quadrática
DEFINIÇÃO Ao construir o gráfico de uma função qua-
Chama-se função quadrática, ou função po- drática y = ax2 + bx + c, notaremos sempre
linomial do 2º grau, qualquer função f de IR que:
em IR dada por uma lei da forma se a > 0, a parábola tem a concavidade
f(x) = ax2 + bx + c, onde a, b e c são núme- voltada para cima;
ros reais e a 0. se a < 0, a parábola tem a concavidade
Vejamos alguns exemplos de função qua- voltada para baixo;
dráticas:
ZERO E EQUAÇÃO DO 2º GRAU
f(x) = x2 -1, onde a = 1, b = 0 e c = -1 Chama-se zeros ou raízes da função poli-
nomial do 2º grau f(x) = ax2 + bx + c , a 0,
f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5 os números reais x tais que f(x) = 0.
Então as raízes da função
f(x) = - x2 + 8x, onde a = 1, b = 8 e c = 0 f(x) = ax2 + bx + c são as soluções da equa-
ção do 2º grau ax2 + bx + c = 0, as quais
f(x) = -4x2, onde a = - 4, b = 0 e c = 0 são dadas pela chamada fórmula de Bhas-
kara:
GRÁFICO
O gráfico de uma função polinomial do 2º
grau, y = ax2 + bx + c, com a 0, é uma
curva chamada parábola. Temos:
Exemplo:
Vamos construir o gráfico da função
y = x2 + x:
Primeiro atribuímos a x alguns valores, de- Observação
pois calculamos o valor correspondente de A quantidade de raízes reais de uma função
y e, em seguida, ligamos os pontos assim quadrática depende do valor obtido para o
obtidos. radicando , chamado discri-
minante, a saber:
x y quando ∆ > 0, há duas raízes reais e distin-
-3 6 tas;
-2 2 quando ∆ = 0, há só uma raiz real;
-1 0 quando ∆ < 0, não há raiz real.
COORDENADAS DO VÉRTICE
DA PARÁBOLA
0 0 Quando a > 0, a parábola tem concavidade
1 2 voltada para cima e um ponto de mínimo V;
quando a < 0, a parábola tem concavidade
2 6 voltada para baixo e um ponto de máxi-
mo V.
Em qualquer caso, as coordenadas de V
Observação: são . Veja os gráficos:

2. 2ª quando a < 0,
a<0
IMAGEM
CONSTRUÇÃO DA PARÁBOLA
O conjunto-imagem Im da função
É possível construir o gráfico de uma função
y = ax2 + bx + c, a 0, é o conjunto dos va-
do 2º grau sem montar a tabela de pares
lores que y pode assumir.
(x, y), mas seguindo apenas o roteiro de
Há duas possibilidades:
observação seguinte:
1. O valor do coeficiente a define a concavi-
1ª - quando a > 0,
dade da parábola;
2. Os zeros definem os pontos em que a pa-
rábola intercepta o eixo dos x;
3. O vértice V indica o ponto
a>0
de mínimo (se a > 0), ou máximo (se a < 0);

3. 4. A reta que passa por V e é paralela ao quando < 0
eixo dos y é o eixo de simetria da parábola; y>0 x1 < x < x2
5. Para x = 0 , temos y = a · 02 + b · 0 + c = y<0 (x < x1 ou x > x2)
c; então (0, c) é o ponto em que a parábola
corta o eixo dos y.
SINAL
Consideramos uma função quadrática y =
f(x) = ax2 + bx + c e determinemos os valo-
res de x para os quais y é negativo e os va-
lores de x para os quais y é positivos.
Conforme o sinal do discriminante
∆ = b2 - 4ac, podemos ocorrer os seguintes
casos:
1º - ∆ > 0
Nesse caso a função quadrática admite dois
zeros reais distintos (x1 x2). a parábola
intercepta o eixo Ox em dois pontos e o si-
nal da função é o indicado nos gráficos a-
baixo: 2º - ∆ = 0
quando a > 0 quando a > 0
y>0 (x < x1 ou x > x2)
y<0 x1 < x < x2

4. quando a < 0
quando a < 0
3º - ∆ < 0
fonte: somatematica
quando a > 0