O documento discute polinômios, definindo-os como expressões algébricas que envolvem termos com variáveis elevadas a potências inteiras. Aborda o grau de polinômios, propriedades de soma e multiplicação, e equações de 1o e 2o grau, cujos gráficos são retas e parábolas respectivamente.

1. Polinômios.
(Todas as definições a seguir serão válidas para o conjunto dos números reais.)
Os polinômios podem ser definidos da seguinte forma:
p(x) = ao + a 1x + a2x² + a3x³ +...+ anxn
sendo ai números reais chamados de coeficientes (com i = 0,1,2,3,...). O coeficiente a0
é conhecido como coeficiente constante, pois a incógnita que o acompanha tem
expoente nulo .
O grau de um polinômio é definido pela incógnita que tem o expoente de maior
valor e pode ser ordenado de forma crescente ou decrescente. Quando polinômio tem
um ou mais termos nulos, então ele é chamado de incompleto.
Uma das funções polinomiais mais importantes é definida por:
f(x) = a x² + b x + c
chamada de função do segundo grau. O gráfico desta função é a curva plana
denominada parábola, que tem algumas características utilizadas em estudos de
Cinemática, radares, antenas parabólicas e faróis de carros.
O valor numérico de um polinômio é obtido através da substituição da
incógnita pelo número que se deseja. Outras informações sobre os polinômios de
segundo grau se têm ao analisar os gráficos formados. Esta matéria será melhor
tratada na aula de funções.
Vejamos um exemplo:
Exemplo: O valor numérico de p(x)=2x²+7x-12 para x=3 é dado por:
p(3) = 2×(3)²+7×3-12 = 2×9+21-12 = 18+9 = 27
Algumas propriedades dos polinômios
Igualdade de polinômios:
A igualdade se verifica se, e somente se, o grau dos polinômios forem iguais e
seus coeficientes também.

2. Soma de polinômios:
Considere os polinômios p(x) e q(x)
p(x) = ao + a 1x + a2x² + a3x³ +... + anxn
q(x) = bo + b1x + b2x² + b3x³ +... + bnxn
a soma será basicamente somar os coeficientes de mesmo grau. Veja o resultado da
soma:
(p+q)(x) = (ao +bo)+(a1+b1)x+(a2+b2)x²+...+(an+bn)xn
Pode-se definir que a+b = c, sendo assim, temos que a resposta, de forma mais exata,
será:
(p+q)(x) = (co)+(c1)x+(c2)x²+...+(cn)xn
Existem algumas propriedade da soma que são importantes de serem
lembradas. Elas são:
Associativa: Quaisquer que sejam p, q, r em P[x], tem-se que:
(p + q) + r = p + (q + r)
Comutativa: Quaisquer que sejam p, q em P[x], tem-se que:
p+q=q+p
Elemento neutro: Existe um polinômio po(x)=0 tal que
po + p = p
Elemento oposto: Para cada p em P[x], existe outro polinômio q=-p em P[x] tal que
p+q=0
Produto de polinômios
Assim como na soma, o objetivo é apenas multiplicar os coeficientes relativos
ao mesmo grau. Veja o exemplo: sejam os polinômios p(x) e q(x)
p(x) = ao + a 1x + a2x² + a3x³ +...+ anxn
q(x) = bo + b1x + b2x² + b3x³ +...+ bn xn
o resultado será dado por:
r(x) = p(x)·q(x) = co + c1x + c2x² + c3x³ +...+ cnxn
lembrando que o produto deve ser feito de forma distributiva, ou seja, todos
elementos de um polinômio multiplicam todos os elementos do outro polinômio.
Assim como na soma, o produto também tem suas propriedades:

3. Associativa: Quaisquer que sejam p, q, r em P[x], tem-se que:
(p · q) · r = p · (q · r)
Comutativa: Quaisquer que sejam p, q em P[x], tem-se que:
p·q=q·p
Elemento nulo: Existe um polinômio po(x)=0 tal que
po · p = po
Elemento Identidade: Existe um polinômio p1(x)=1 tal que
p1 · p = p
qualquer que seja p em P[x]. A unidade polinomial é simplesmente denotada por p 1=1.
Equações de 1º grau
Uma função do 1º grau é toda função do tipo:
y(x) = ax + b
Onde a ≠ 0
A solução (ou raiz, ou zero) dessa equação é simples, e é obtida isolando-se o x quando
y = 0:
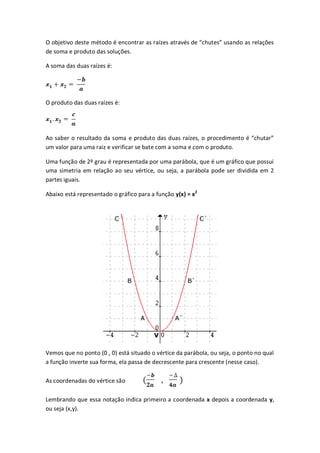
Toda função do 1º grau tem seu gráfico representado por uma reta, por isso também
pode-se chamar de função linear.
Por exemplo, para a função y(x) = 3x -1 seu gráfico é:

4. Os dois pontos principais desse tipo de gráfico são os pontos onde ocorre a reta
intercepta um eixo, nesse caso esses pontos são  (0 , -1) e (1/3 , 0).
Esses pontos são importantes, pois nos dizem como a reta é.
Os coeficientes a e b da função são chamados de coeficientes angular e linear
respectivamente.
O coeficiente angular também é igual a:
a = tg θ
Onde θ é o ângulo formado entre a reta e o eixo x.
Na matéria de laboratório vê-se muitas relações e fenômenos que podem ser descritos
ou aproximados à uma reta.
Equações de 2º grau
Analogamente à função de 1º grau, uma função de 2º grau é toda função do tipo:
y(x) = ax 2 + bx + c
onde a ≠ 0
Existem dois meios principais de se achar as raízes de uma equação de 2º grau.
Por Bhaskara
Esse método se baseia em uma quantidade chamada Delta Δ
As raízes são dadas pela seguinte equação:
Onde Δ = b2 – 4ac
Veja que teremos 2 raízes, ou seja, pontos onde o gráfico intercepta o eixo x. São elas:
e
Por Soma e Produto

5. O objetivo deste método é encontrar as raízes através de “chutes” usando as relações
de soma e produto das soluções.
A soma das duas raízes é:
O produto das duas raízes é:
Ao saber o resultado da soma e produto das duas raízes, o procedimento é “chutar”
um valor para uma raiz e verificar se bate com a soma e com o produto.
Uma função de 2º grau é representada por uma parábola, que é um gráfico que possui
uma simetria em relação ao seu vértice, ou seja, a parábola pode ser dividida em 2
partes iguais.
Abaixo está representado o gráfico para a função y(x) = x2
Vemos que no ponto (0 , 0) está situado o vértice da parábola, ou seja, o ponto no qual
a função inverte sua forma, ela passa de decrescente para crescente (nesse caso).
As coordenadas do vértice são
Lembrando que essa notação indica primeiro a coordenada x depois a coordenada y,
ou seja (x,y).

6. Existem somente 6 tipos de gráficos para uma função de 2º grau, e eles dependem dos
valores de a e de Δ.
Se a > 0  concavidade (boca da parábola) para cima;
Se a < 0  concavidade para baixo;
Se Δ > 0  existem duas raízes reais e distintas;
Se Δ = 0  existem duas raízes reais e idênticas;
Se Δ < 0  não existe raiz real.
Dizemos que uma função é positiva em tal intervalo se naqueles pontos seu valor for
maior que 0.
Dizemos que uma função é negativa em tal intervalo se naqueles pontos seu valor for
menor que 0.
Por exemplo, para a função y(x) = x2 - 4x + 3
Suas raízes são x1 = 1 e x2 = 3
Seu gráfico (gerado no Origin) é:

7. Model Polynomi
25 Adj. R-Squ 0,9988
Value Standard Er
B Intercept 2,8475 0,13219
20 B B1 -3,977 0,05352
B B2 1,0011 0,01097
15
B
Polynomial Fit of B
Y(x)
10
5
0
-5
-4 -2 0 2 4 6 8
X
Por enquanto, esses valores na tabela não nos interessam. Os pontos foram fornecidos
por mim, enquanto que a reta vermelha representa o “fit” (ou ajuste) dos pontos à
uma parábola média. Veja que nos pontos (1,0) e (3,0) a curva intercepta o eixo x.
Vejam também que nos intervalos do eixo x (- , 1) e (3, + ) a curva está acima do
eixo x, isso significa que ela é positiva. Já no intervalo (1,3) a curva passa por baixo,
mostrando que ela é negativa.