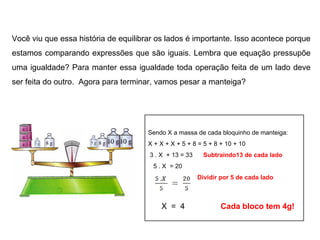
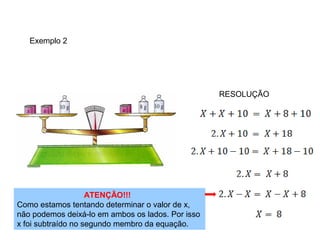
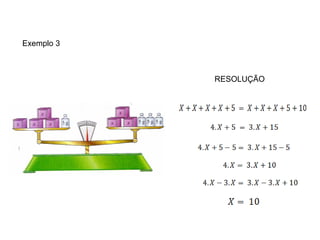
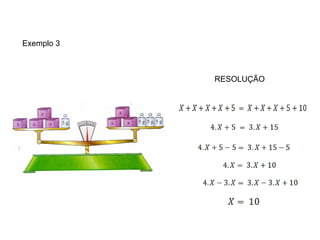
O documento ensina sobre equações do 1o grau usando exemplos de pesagem de alimentos. Mostra como equilibrar os lados de uma equação para determinar o peso desconhecido de cada item, como 150g para cada pote de mel e 4g para cada bloco de manteiga. Explica que operações feitas em um lado devem ser feitas no outro para manter a igualdade da equação.

1. MATEMÁTICA
O Manuel quer terminar de fazer os pães e para isso tem que
pesar o mel e a manteiga. Vamos lá?
Agora vamos pesar o mel, já está tudo na balança. Lembre-se
que se queremos saber o peso de cada pote só pode ficar um
pote de um lado da balança!
Os potes de mel são os temos desconhecidos, logo:
Observe este outro exemplo:
X + X + 50 = X + 200
2. X + 50 = X + 200 (Tira-se 50 g de cada lado da balança)
2. X + 50 - 50 = X + 200 – 50
2. X = X + 150 (Tira-se um pote de mel, nosso x, de cada
lado)
2. X – X = X – X + 150
X = 150g Cada pote de mel tem 150 gramas

2. MATEMÁTICA
Você viu que essa história de equilibrar os lados é importante. Isso acontece porque
estamos comparando expressões que são iguais. Lembra que equação pressupõe
uma igualdade? Para manter essa igualdade toda operação feita de um lado deve
ser feita do outro. Agora para terminar, vamos pesar a manteiga?
Sendo X a massa de cada bloquinho de manteiga:
X + X + X + 5 + 8 = 5 + 8 + 10 + 10
3 . X + 13 = 33 Subtraindo13 de cada lado
5 . X = 20
Dividir por 5 de cada lado
X = 4 Cada bloco tem 4g!

3. Equações do 1˚ Grau – Outros Exemplos
Indicando a massa, em gramas de cada cubo por x, vamos determinar
a equação sugerida pela balança.
Exemplo 1
RESOLUÇÃO

4. Exemplo 2
RESOLUÇÃO
ATENÇÃO!!!
Como estamos tentando determinar o valor de x,
não podemos deixá-lo em ambos os lados. Por isso
x foi subtraído no segundo membro da equação.

5. Exemplo 3
RESOLUÇÃO

6. Exemplo 3
RESOLUÇÃO