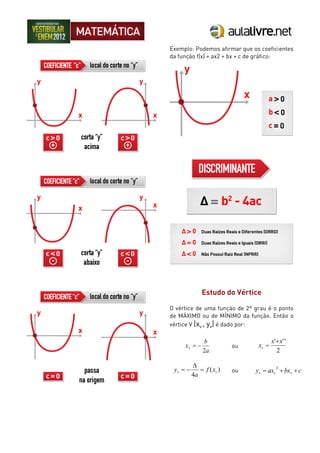
O documento discute funções do segundo grau, incluindo sua forma geral, estudo dos coeficientes, vértice e forma fatorada. Exemplos ilustram como calcular o vértice e transformar uma função em sua forma fatorada. Exercícios propõem problemas envolvendo funções quadráticas.

1. Aula 03
Funções do 2º grau
Forma geral
Onde “a”,” b” e “c” pertencem ao conjunto de
números reais e a 0
Estudo dos Coeficientes

2. Exemplo: Podemos afirmar que os coeficientes
da função f(x) = ax2 + bx + c de gráfico:
Estudo do Vértice
O vértice de uma função de 2º grau é o ponto
de MÁXIMO ou de MÍNIMO da função. Então o
vértice V (xv , yv) é dado por:
a
b
xv
2

2
''' xx
xv


)(
4
vv xf
a
y 

 cbxaxy vvv 
2
ou
ou

3. Forma fatorada da função
1º) Elabora-se a forma f(x) = ( ).( ).( )...
O número de fatores é igual ao número de
raízes.
2º) Em cada parêntese coloca-se “x”
acompanhado de uma raiz com o sinal trocado.
3º) Resolve-se o produto entre os parênteses.
O termo independente deve coincidir com o
corte no eixo vertical.
Exemplo:
f(X)= (X+2).(X-1)
f(X)= X2
– X + 2X – 2
f(X)= X2
+ X – 2
O termo independente “- 2” está de acordo
com o gráfico? E se não coincidir?
Deve-se multiplicar toda a função pelo fator
adequado de forma que o termo independente
coincida com o “corte” no eixo “y”.
Exercícios
1) (UFRGS RS) O movimento de um projétil,
lançado para cima verticalmente, é descrito
pela equação y= - 40x² + 200x onde y é a
altura, em metros, atingida pelo projétil x
segundos após o lançamento. A altura máxima
atingida e o tempo que esse projétil
permanece no ar correspondem,
respectivamente, a:
a) 6,25 m, 5s
b) 250 m, 0 s
c) 250 m, 5 s
d) 250 m, 200 s
e) 10.000 m, 5 s
2) (UM SP) O vértice da parábola y = x2
+ bx + 6
está no ponto (2, k). O valor de k é:
a) 1
b) 2
c) 3
d) 4
e) 5
3) (UFES ES) O vértice da parábola de equação
y = 2x2
– 4x + t será um ponto do eixo das
abscissas se o valor de t for igual a:
a) 2
b) 1
c) – 1
d) – 2
e) – 3
4) (FAFI MG) O gráfico de uma função
f(x) = a2
+ bx + c está representado abaixo.
Podemos afirmar que:
a) a<0; b<0; e c<0
b) a<0; b<0; e c>0
c) a<0; b>0; e c <0
d) a<0; b>0; e c >0
e) a>0; b<0; e c<0

4. 5) (UFPA PA) A parábola de equação
y = x2 – 5x – 14 é simétrica em relação à reta:
a) y = x
b) x = - 2
c) x = 7
d) x = 5
2
e) y = - x
Gabarito
1 – C 2 – B 3 – A 4 – D 5 –D