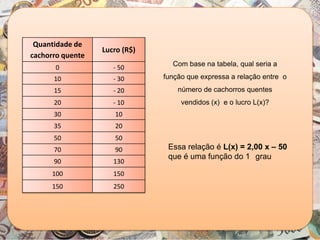
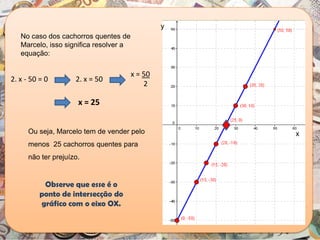
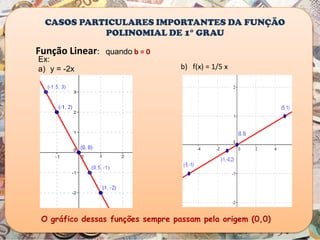
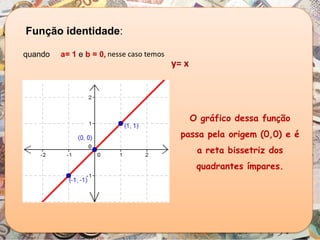
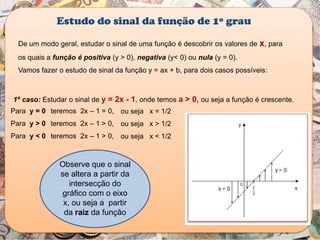
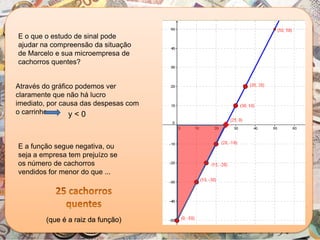
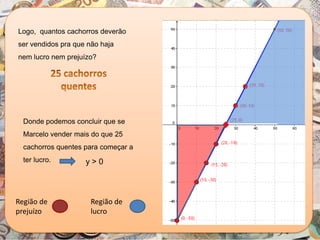
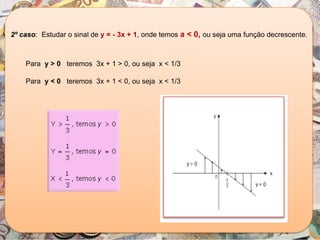
O documento aborda a importância da função polinomial do 1º grau no ensino de contabilidade, utilizando a análise custo/volume/lucro como aplicação prática. Através de um exemplo com um vendedor de cachorro quente, é explicado como calcular o lucro e o ponto de equilíbrio, demonstrando a relação entre vendas e lucro. Além disso, apresenta o estudo do sinal das funções do 1º grau, destacando como interpretar os resultados em contextos contábeis.

1. Autoras:
Fernanda Souza
Katia Dutra

2. A Contabilidade e a Matemática compõem a essência do desenvolvimento
profissional do aluno do curso técnico em contabilidade.
Pensando nisso, vamos nessa aula aprofundar o estudo da função
polinomial o 1 grau, ou função afim e para isso vamos observar uma
aplicação prática da análise custo/volume/lucro no ensino de funções
polinomiais do 1 grau.
Vamos lá?
Vamos começar?

3. Lucro é a diferença entre as despesas e as receitas, não é?
Mas você sabia existem diferentes categorias de lucro?

5.  o preço de um produto depende da
demanda do mercado;
a conta mensal de energia depende do
consumo da população;
 o valor de um bem depende do seu
tempo de vida útil;
 o custo total de uma indústria depende
da quantidade de produto fabricada;
 a receita e o lucro das vendas dependem
da quantidade que foi vendida, etc.
Já vimos que o conceito de função pode ser visto
em várias exemplos de aplicações contábeis, como:

6. Vamos realizar a análise de custo/volume/lucro e das funções matemáticas relativas
uma microempresa de produção e venda de cachorros quente. Isso pode ser feito
através de uma visão contábil e de uma visão matemática, apresentando dados e
resultados.
Veja nessa aula!
Como encontrar o zero de uma função do 1 grau? E
o estudo do sinal da função afim? Será que eles
podem nos ajudar a na análise de custo/volume/lucro?

7. Fique por dentro
Observe a seguinte situação:
Marcelo decidiu vender cachorro quente em um carrinho em dias de jogos
importantes no Maracanã. Ele aluga o carrinho por R$ 50,00 ao dia. Ele vende
cada cachorro quente por R$ 5,00 e seus custos
(condimentos, salsicha, molho, guardanapo e gás) são, em média cerca de
R$3,00 por unidade. Logo o lucro de um único cachorro quente é de R$ 2,00.
Para facilitar a compreensão de sua contabilidade, Marcelo construiu uma tabela e
um gráfico.

8. Quantidade de
cachorro quente
Lucro (R$)
0 - 50
10 - 30
15 - 20
20 - 10
30 10
35 20
50 50
70 90
90 130
100 150
150 250
Com base na tabela, qual seria a
função que expressa a relação entre o
número de cachorros quentes
vendidos (x) e o lucro L(x)?
Essa relação é L(x) = 2,00 x – 50
que é uma função do 1 grau

9. Quantos cachorros quentes deverão ser
vendidos para que Marcelo não tenha
lucro nem prejuízo?
Matematicamente, encontrar o valor de x que torna a função nula é encontrar o zero da
função do 1° grau.
Temos nesse caso de descobrir x
para que L(x), o lucro, seja zero.

10. O zero ou raiz da função polinomial de 1º grau
O zero ou raiz de uma função é o valor real x, tal que y = 0.
Para encontrarmos o zero da função polinomial de 1º grau y = ax +
b (a ≠ 0) basta resolver a equação do 1º grau ax + b = 0 cuja
solução é :

11. No caso dos cachorros quentes de
Marcelo, isso significa resolver a
equação:
Ou seja, Marcelo tem de vender pelo
menos 25 cachorros quentes para
não ter prejuízo.
Observe que esse é o
ponto de intersecção do
gráfico com o eixo OX.
x
y
2. x - 50 = 0 2. x = 50
x = 25
x = 50
2

12. a) y= 5x – 2
b) f(x) =
y= 0 se 5x – 2 = 0, para isso temos
f(x) = 0 se então x = 12
Vamos determinar o zero de outras funções do 1 grau?
Veja alguns exemplos.

13. CASOS PARTICULARES IMPORTANTES DA FUNÇÃO
POLINOMIAL DE 1° GRAU
Função Linear:
O gráfico dessas funções sempre passam pela origem (0,0)
quando b = 0
Ex:
a) y = -2x b) f(x) = 1/5 x

14. O gráfico desse tipo de
função é uma reta paralela
ao eixo OX.
Função constante:
quando a = 0
Ex:
a) f(x) = 3
b) y = - 5
2
f(x) = 3
y = - 5
2

15. nesse caso temos
Função identidade:
quando a= 1 e b = 0,
O gráfico dessa função
passa pela origem (0,0) e é
a reta bissetriz dos
quadrantes ímpares.
y= x

16. De um modo geral, estudar o sinal de uma função é descobrir os valores de x, para
os quais a função é positiva (y > 0), negativa (y< 0) ou nula (y = 0).
Vamos fazer o estudo de sinal da função y = ax + b, para dois casos possíveis:
Estudo do sinal da função de 1º grau
1º caso: Estudar o sinal de y = 2x - 1, onde temos a > 0, ou seja a função é crescente.
Observe que o sinal
se altera a partir da
intersecção do
gráfico com o eixo
x, ou seja a partir
da raiz da função
ou seja x = 1/2Para y = 0 teremos 2x – 1 = 0,
Para y > 0 teremos 2x – 1 > 0, ou seja x > 1/2
Para y < 0 teremos 2x – 1 > 0, ou seja x < 1/2

17. E o que o estudo de sinal pode
ajudar na compreensão da situação
de Marcelo e sua microempresa de
cachorros quentes?
Através do gráfico podemos ver
claramente que não há lucro
imediato, por causa das despesas com
o carrinho.
E a função segue negativa, ou
seja a empresa tem prejuízo se
os número de cachorros
vendidos for menor do que ...
(que é a raiz da função)
y < 0

18. Logo, quantos cachorros deverão
ser vendidos pra que não haja
nem lucro nem prejuízo?
Donde podemos concluir que se
Marcelo vender mais do que 25
cachorros quentes para começar a
ter lucro. y > 0
Região de
prejuízo
Região de
lucro

19. 2º caso: Estudar o sinal de y = - 3x + 1, onde temos a < 0, ou seja uma função decrescente.
Para y > 0 teremos 3x + 1 > 0, ou seja x < 1/3
Para y < 0 teremos 3x + 1 < 0, ou seja x < 1/3

20. https://www.youtube.com/watch?v=QwFC3YsBWZY
Vale a pena assistir a essa vídeoaula
para entender melhor a função do 1
grau.

21. Navegando ...
Atividades sobre função afim a serem resolvidas no próprio site:
http://www.dmm.im.ufrj.br/projeto/projetoc/precalculo/sala/conteudo/capitulos/cap81.html
Nesta página, há atividades em flash e problemas referentes a variação de função afim:
http://www.uff.br/cdme/afim/afim-html/AP1.html

22. Agora é sua vez!
1. Os gastos de consumo (C) de uma família e sua renda (x) são tais que
.8,02000 xC
Podemos afirmar que:
(a) se a renda diminui em 500, o consumo aumenta 500.
(b) se a renda diminui em 500, o consumo diminui em 500.
(c) se a renda aumenta em 1 000, o consumo aumenta em 800.
(d) se a renda diminui em 1 000, o consumo diminui em 2 800.
(e) se a renda dobra o consumo dobra.

23. 2. (EEM-SP) O Valor atual de uma máquina é R$ 10000,00. Estima-se que, após 10 anos de
uso, seu valor cairá pra R$ 1000,00. Escreva uma função linear que represente o valor V dessa
máquina em função do tempo t, medido em anos.

24. Confira suas
respostas!
Então? Como foi o seu desempenho?
1. Letra c
2. V = - 100t + 10000

25. Referências Bibliográficas
1.Site: http://www.slideshare.net/contacontabil/contabilidade-bsica-
resumo?from_search=2, acessado em 22/07/2013, 11:53h.
2. GIOVANNI JÚNIOR, José Ruy e CASTRUCCI Benedicto . A Conquista da Matemática, 6º ano.
São Paulo: FTD, 2009
3. SMOLE, Katia, ,KIYUKAWA, Rokusaburo. Matemática, vol. 1. São Paulo: Editora Saraiva, 1998.
4. SILVEIRA, Ênio e MARQUES, Cláudio. Matemática vol. 1. São Paulo: Moderna, 1995.