Este documento contém uma série de exercícios matemáticos sobre funções, incluindo identificar funções, determinar domínios e contradomínios, representar funções graficamente e algebraicamente, calcular imagens e objetos, e resolver problemas envolvendo gráficos de distância versus tempo.

1. Ficha de Trabalho n.º___
1. Indica justificando, quais das correspondências seguintes são funções?
2. Considera a função definida pelo diagrama de setas.
a) Indica o domínio e o contradomínio da função.
b) Representa a função por uma expressão analítica.
3.Considera a correspondência g , de A em B, que a cada pessoa faz corresponder a sua
idade em anos, definida pelo diagrama:
3.1. Será esta correspondência uma função? Justifica a
tua resposta.
3.2. No caso da correspondência g ser uma função
indica:
a) o domínio;
b) o contradomínio;
c) o conjunto de chegada;
d) as variáveis independente e dependente;
e) a imagem do objeto João;
f) o objeto que tem por imagem 15.
Matemática
Nome: __________________________________
Ano: _____ Turma: ____ Data: ___/___/______

2. 3.3.Completa:
a)   .......Mariag b)   16....... g
4. Considera a função definida por: y = 4x + 2
a) Determina a imagem do objecto 5.
b) Determina o objecto cuja imagem é 402.
5. Considera a função y = 2x – 10.
5.1. Completa a tabela.
Objeto Imagem
-3
1
6,2
-22
6. Dadas as funções: f(x) = 2x + 3 e g(x) = -x + 1. Calcula f(2), f(-3), g(5) e g(-2).
7. Numa experiência, a hora é representada por h e a temperatura por T .
A função que a cada h faz corresponder o valor de T é dada pela expressão 53  hT .
Sabendo que o domínio da função é }7,6,5,3{ , o contradomínio da função é:
}16,13,10,4{'
D }32,31,30,28{'
D }32,15,22,12{'
D }26,23,20,14{'
D
8. Considera o referencial (OX, OY).
8.1. Representa no referencial os pontos E = (5, 0);
F= (-1, 2); G = (0; 3).
8.2. Indica as coordenadas dos pontos A, B, C e D.
8.3. Indica um ponto de abcissa superior à ordenada.
8.4. Indica um ponto cujo valor absoluto da abcissa é igual
ao valor absoluto da ordenada.
8.5. Marca um ponto S de coordenadas simétricas.

3. 9. Representa no mesmo referencial as funções:
10. Seja f a função definida por 2
2
1
)(  xxf de domínio Df=-2, 0, 2, 4.
a) Constrói o diagrama de setas para a função f.
b) Representa graficamente a função f.
c) A função f é uma função afim? Porquê?

4. 11. Considera a seguinte função f definida pelo
gráfico:
Indica:
11.1. O domínio da função;
11.2. O contradomínio da função;
11.3. A imagem do objeto 5;
11.4. O objeto cuja imagem é 1;
11.5. Dois objetos com a mesma imagem.
12. Seja a função j dada pela expressão algébrica j(x) = 2x +3.
Sabendo que o domínio da função é }7,6,5,3{ , determina o seu contradomínio.
13.
14. Considera a figura ao lado, onde:
- [ABFG] é um quadrado de área 36;
- [ BCDE] é um quadrado de área 64;
- F é um ponto do segmento de recta [BE].
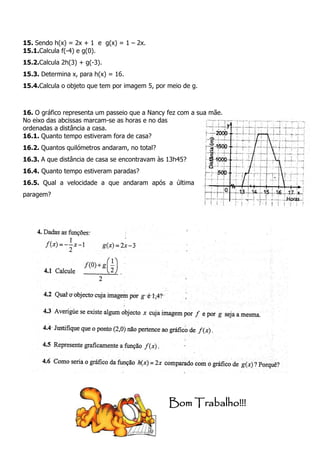
14.1.Qual é a área total das zonas sombreadas da figura?
(A) 64 (B) 66 (C) 68 (D) 70
14. Determina o valor exacto de EG. Apresenta todos os cálculos que efectuares.

5. 15. Sendo h(x) = 2x + 1 e g(x) = 1 – 2x.
15.1.Calcula f(-4) e g(0).
15.2.Calcula 2h(3) + g(-3).
15.3. Determina x, para h(x) = 16.
15.4.Calcula o objeto que tem por imagem 5, por meio de g.
16. O gráfico representa um passeio que a Nancy fez com a sua mãe.
No eixo das abcissas marcam-se as horas e no das
ordenadas a distância a casa.
16.1. Quanto tempo estiveram fora de casa?
16.2. Quantos quilómetros andaram, no total?
16.3. A que distância de casa se encontravam às 13h45?
16.4. Quanto tempo estiveram paradas?
16.5. Qual a velocidade a que andaram após a última
paragem?
Bom Trabalho!!!