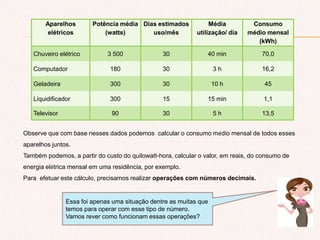
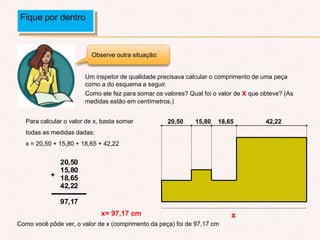
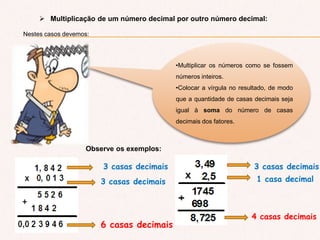
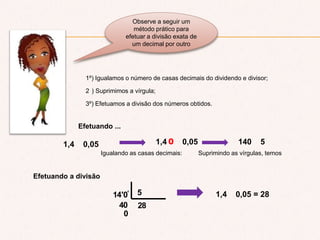
O documento aborda a importância do consumo de energia elétrica e apresenta métodos para calcular o consumo mensal com base na potência dos aparelhos. Além disso, detalha operações matemáticas com números decimais, incluindo adição, subtração, multiplicação e divisão, com exemplos práticos. O texto conclui ressaltando a utilidade desse conhecimento em contextos técnicos e acadêmicos.

1. MATEMÁTICA PARA MECÂNICA
Autoras:
Fernanda Souza
Katia Dutra

2. Vamos começar?
O consumo de energia elétrica é uma preocupação do mundo moderno.
Se analisarmos uma conta de luz e soubermos a potência de um equipamento
elétrico, poderemos anotar a frequência de uso desses aparelhos para construir uma
tabela como a que vemos a seguir:

3. Observe que com base nesses dados podemos calcular o consumo médio mensal de todos esses
aparelhos juntos.
Também podemos, a partir do custo do quilowatt-hora, calcular o valor, em reais, do consumo de
energia elétrica mensal em uma residência, por exemplo.
Para efetuar este cálculo, precisamos realizar operações com números decimais.
Essa foi apenas uma situação dentre as muitas que
temos para operar com esse tipo de número.
Vamos rever como funcionam essas operações?
Aparelhos
elétricos
Potência média
(watts)
Dias estimados
uso/mês
Média
utilização/ dia
Consumo
médio mensal
(kWh)
Chuveiro elétrico 3 500 30 40 min 70,0
Computador 180 30 3 h 16,2
Geladeira 300 30 10 h 45
Liquidificador 300 15 15 min 1,1
Televisor 90 30 5 h 13,5

4. Um inspetor de qualidade precisava calcular o comprimento de uma peça
como a do esquema a seguir.
Como ele fez para somar os valores? Qual foi o valor de x que obteve? (As
medidas estão em centímetros.)
Para calcular o valor de x, basta somar
todas as medidas dadas:
x = 20,50 + 15,80 + 18,65 + 42,22
x= 97,17 cm
Fique por dentro
Observe outra situação:
+
20,50
15,80
18,65
42,22
97,17
Como você pôde ver, o valor de x (comprimento da peça) foi de 97,17 cm
x
42,2218,6515,8020,50

5. Para ADIÇÃO ou SUBTRAÇÃO de números decimais, devemos observar que:
Os algarismos que ocupam a mesma ordem (unidade,
dezena, centena, etc.) devem ficar na mesma coluna, com
uma virgula alinhada à outra (vírgula embaixo de vírgula).
Depois disso, basta adicionar e subtrair normalmente.
Por fim, no resultado, a vírgula se mantém alinhada com as
demais.

6. 1 , 2 8 + 2,6 + 0 , 0 3 8 =1 , 2 8 2 , 6
0
0 , 0 3 8
+
_________
3 , 9 1 8
3,918
0
0
Clique e veja
alguns exemplos:
35,4 + 0,75 + 47 = 83,15
83,15
+
35,40
0,75
47,00
9 – 0,987 = 8,013
8,013
_ 9,000
0,987

7. O estudo da MULTIPLICAÇÃO de números decimais pode ser dividido em dois casos:
Clique nos exemplos abaixo e
observe que para multiplicar um
número decimal por 10, 100 e
1000, basta deslocar a vírgula
uma, duas, três posições para a
direita, respectivamente.
 Multiplicação por 10, por 100, por 1000.
1,349 x 10 =
1,349 x 100 =
1,349 x 1000 =
134 9,
134 9
134 9
,
,
A virgula deslocou
uma casa decimal
A virgula deslocou
duas casas decimais
A virgula deslocou
três casas decimais

8.  Multiplicação de um número decimal por outro número decimal:
Nestes casos devemos:
•Multiplicar os números como se fossem
números inteiros.
•Colocar a vírgula no resultado, de modo
que a quantidade de casas decimais seja
igual à soma do número de casas
decimais dos fatores.
Observe os exemplos:
3 casas decimais
3 casas decimais
6 casas decimais
3 casas decimais
1 casa decimal
4 casas decimais

10. Até aqui, já vimos como efetuar as operações de adição, subtração e multiplicação de números
decimais.
E na DIVISÃO como devemos proceder?
Em muitas disciplinas técnicas você trabalha com conversão de medidas. Essas, por sua vez,
exigem operações com números decimais e, em especial, a divisão.
Vamos rever como efetuar a divisão?
Nos números fracionários, multiplica-se o numerador da fração
por 25,4 e divide-se o resultado pelo denominador.

11. O estudo da DIVISÂO de números decimais pode ser dividido nos seguintes casos:
 Divisão por 10 , 100 e 1000:
Para dividir por 10, 100 e 1000 devemos deslocar a
vírgula uma, duas, três posições para a esquerda,
respectivamente. Quer ver melhor? Clique e observe os
exemplos a seguir!
134,9 ÷ 10 = 134 9,
134,9 ÷ 100 = 134 9,
134,9 ÷ 1000 = 134 9,0

12.  Divisão de um número decimal por outro número decimal:
1º caso: Divisão exata
Considere a divisão entre 1,4 : 0,05.
Transformando em frações decimais temos:
Os outros casos de divisão podem ser estudados em dois casos: o da divisão exata e o da
divisão não exata.
Você deve ter percebido que a divisão ficou muito fácil ao
transformarmos os números decimais em frações

13. Observe a seguir um
método prático para
efetuar a divisão exata de
um decimal por outro
1º) Igualamos o número de casas decimais do dividendo e divisor;
2 ) Suprimimos a vírgula;
3º) Efetuamos a divisão dos números obtidos.
Efetuando ...
1,4 0,05
Igualando as casas decimais:
1,4 0,050
Suprimindo as vírgulas, temos
140 5
Efetuando a divisão
0
40 28
514'0' 1,4 0,05 = 28

14. http://www.youtube.com/watch?v=74y69o4cnHM
Entenda melhor a divisão de
decimais assistindo a essa
vídeoaula.

15. 2º caso: Divisão não exata
No caso da divisão não exata calculamos o quociente aproximado.
Seja por exemplo a divisão de 66 por 21.
6
90
30 3,14
66' 21
Determinar um quociente com aproximação de
décimos, centésimos ou milésimos significa parar a
divisão ao atingir a primeira, segunda ou terceira casa
decimal do quociente, respectivamente.
Exemplos:
13 ÷ 7 = 1, 8 ( aproximação de décimos )
13 ÷ 7 =
13 ÷ 7 =
1,
1,
85 ( aproximação de centésimos )
857 ( aproximação de milésimos )

16. http://www.youtube.com/watch?v=JjSUgr6pZI0

17. Para finalizar, vamos recordar a potenciação e a radiciação de números decimais. Vamos lá?
Potenciação de números decimais
As potências nas quais a base é um número decimal e o expoente é um numero natural, utilizamos a
mesma regra de potenciação.
Multiplicamos a base por
ela mesma, quantas
vezes for o expoente.

18. (0,7)³ = 0,7 x 0,7 x 0,7 = 0,343
3 fatores
(0,5) =
5
0,5 x 0,5 x 0,5 x 0,5 x 0,5
5 fatores
= 0,03125
(3,2)²= 3,2 x 3,2
2 fatores
= 10,24
Clique e observe os exemplos:

19. A raiz quadrada de um número decimal pode ser
determinada com facilidade, transformando o
número em uma fração decimal.
Veja os exemplos:
Raiz Quadrada de números decimais
E lembre: todas essas operações serão muito utilizadas ao
longo de todo o seu curso técnico!

20. Navegando...
Fique mais por dentro dos decimais. Acesse:
http://www.slideshare.net/guestdc3a85/nmeros-racionais-expressos-na-forma-decimal-2519868
História dos Números Decimais da Turma da Mônica:
http://www.slideshare.net/kov0901/histria-dos-nmeros-decimais-6023932

21. Agora é sua vez!
Teste os seus
conhecimentos.

22. 3. Com pedaços de arame que medem 22,6 cm e 13,8 cm, podemos construir o esqueleto de um
bloco retangular, como você vê na figura. Quantos centímetros desse arame são necessários
para essa construção?
13,8 cm
13,8 cm
22,6 cm
2. Calcule o comprimento (L) de uma correia aberta que deverá ligar duas polias de diâmetros
diferentes (15 cm e 20 cm) e com distância entre os eixos de 40 cm.
Para calcular esse comprimento vamos utilizar a seguinte fórmula:
Onde R é o raio maior, r o raio menor e c a distância entre os eixos.

23. 4. Ao iniciar uma viagem, Valdir abasteceu o tanque de combustível do seu carro, que estava
totalmente vazio, e pagou R$ 162,80 pelo abastecimento. Se o litro de combustível custa R$ 2,96,
quantos litros cabem no tanque do carro de Valdir?
5. Calcule o comprimento da correia aberta que liga duas polias iguais com 30 cm de diâmetro e com a
distância entre eixos de 70 cm.
Para resolver esse problema você vai aplicar: L = p x d + 2 x c
Onde L é o comprimento total da correia; p x d é o perímetro da circunferência e c é a distância entre
os centros dos eixos.

24. Gabarito
Confira suas
respostas!
1) 1,425 mm
2) 142,27 cm
3) 200,8 cm
4) 55 litros
5) 234,20 cm

25. Referências Bibliográficas
1. FRANÇA, Hélio. Mecânica: Máquinas Térmicas, Hidráulicas e Pneumáticas. Rio de Janeiro:
FAETEC- ETER, 2008
2. GIOVANNI JÚNIOR, José Ruy e CASTRUCCI Benedicto . A Conquista da Matemática, 6º ano.
São Paulo: FTD, 2009
3. SILVEIRA, Ênio e MARQUES, Cláudio. Matemática vol. 1. São Paulo: Moderna, 1995
4. Telecurso Profissionalizante de Mecânica, NOVO TELECURSO 2000 – teleaula nº 8 de Cálculo
Técnico. Fundação Roberto Marinho.