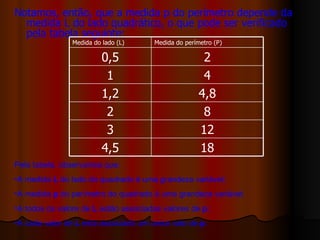
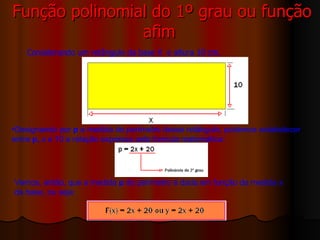
1) O documento discute funções matemáticas e fornece exemplos de funções polinomiais de primeiro grau. 2) Funções polinomiais de primeiro grau, também chamadas de funções afins, relacionam duas variáveis através de uma equação da forma y = ax + b. 3) O gráfico de uma função polinomial de primeiro grau no plano cartesiano é uma reta, cuja inclinação e posição dependem dos coeficientes a e b.

1. Funções

2. Noção intuitiva de função Com frequência encontramos em matemática relação entre duas grandezas variáveis. Observemos uma situação Exemplos: Seja um quadrado cujo o lado mede L . Designando por p a medida do perímetro desse quadrado, podemos estabelecer entre p e L a seguinte relação expressa pela formula matemática: L L

3. Notamos, então, que a medida p do perímetro depende da medida L do lado quadrático, o que pode ser verificado pela tabela seguinte: Pela tabela, observamos que: A medida L do lado do quadrado é uma grandeza variável; A medida p do perímetro do quadrado é uma grandeza variável; A todos os valore de L estão associadas valores de p ; A cada valor de L esta associado um único valo de p . 18 4,5 12 3 8 2 4,8 1,2 4 1 2 0,5 Medida do perímetro (P) Medida do lado (L)

4. Dizemos, então: A medida do perímetro de um quadrado e dada em função da medida L do lado. A relação p = 4 . L chama-se Lei da associação ou fórmula matemática desta função Na lei de associação dessa função temos:

5. Função polinomial do 1º grau ou função afim Considerando um retângulo da base X e altura 10 cm. Designando por p a medida do perímetro desse retângulo, podemos estabelecer entre p, x e 10 a relação expressa pela formula matemática: Vemos, então, que a medida p do perímetro é dada em função da medida x da base, ou seja:

6. Designando por S a área desse retângulo, podemos estabelecer entre S, x e 10 a relação expressa pela formula matemática: Verificamos também, que a área S é dada em função da medida x da base, ou seja: Observamos, então que em ambos os casos o 2º membro da fórmula matemática que representa a função é um Polinômio do 1 grau na variável x.

7. Definição Na sentença matemática y = ax + b, as letras x e y representam as variáveis enquanto a e são denominadas coeficientes . Assim, são funções do 1º grau: F(x) = 2x + 3 (a = 2 e b = 3) y = -3x (a = -3 e b = 0) F9x) = 5x – 1 (a = 5 e b = - 1 ) y = 1 - 2x ( a = -2 e b = 1) 3 3

8. Observações 1ª) No caso de a ≠ o e b ≠ 0, a função polinomial do 1ª grau recebe o nome de Função afim. exemplos: f(x)= 1 x -3 (a = 1 e b = -3) y = 7 – x (a = -1 e b = 7) 2 2 2ª) No caso de a ≠ 0 e b = 0, a função polinomial do 1ª grau recebe o nome de função linear. exemplos: f(x) = -8x (a = -8 e b = 0) y = 3 x ( a = 3 e b = 0 ) 2 2

9. Gráfico no sistema cartesiano ortogonal 1º caso: a > 0 Vamos construir, num sistema cartesiano ortogonal, o gráfico da função f(x) = 2x – 1 (ou y = 2x -1). 3 2 1 1 -1 0 -3 -1 -5 -2 y = f(x) x

10. Você nota que : O gráfico da função f(x0 = 2x – 1 e um reta. D= IR e Im = IR Sendo o gráfico da função uma reta, basta consideramos dois pontos (x, y) do plano cartesiano para construir o gráfico. A = 2 > 0 Considered dois valores do domínio D ( 1 e 2 por exemplo , 1 > 2), temos: f(1) = 1 } f(1) < f(2)-> a função é crescente . f (2) = 3 } A reta corta o eixo y no ponto de ordenada b.

11. Bibliografia GIOVANNI, José Ruiy; BONJORNO, José Roberto; e GIVANNI Jr. José Ruy. Matemática Fundamental, volume único. FTD