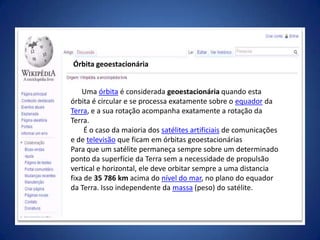
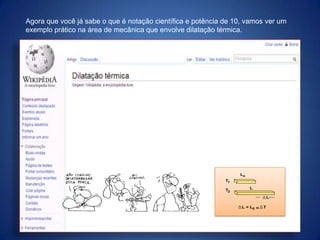
O documento aborda a notação científica e potências de 10, que facilitam a representação de números muito grandes ou muito pequenos, exemplificando com a carga de partículas e distâncias astronômicas. A notação científica é descrita como uma forma de simplificar números, padronizando sua representação e deixando clara sua ordem de grandeza. Além disso, apresenta aplicações práticas em cálculos relacionados à dilatação térmica de materiais.

1. Autoras:
Fernanda Souza
Katia Dutra

2. Vamos começar?
Muitas vezes, temos que escrever números grandes demais ou muito pequenos.
Imagine que você tenha que expressar medidas grandiosas como:
A distância entre a Terra e o Sol

3. Ou mínimas como a carga de um elétron.

4. Fica mais fácil e compacto expressar esses
tipos de medidas se utilizarmos as potências
de 10 e a notação científica.
Vamos rever, então, as potências na base 10 e a notação
científica que muito nos ajudarão na simplificação da escrita e de
cálculos envolvendo esse tipo de número com muitas ordens.

5. Fique por dentro
O que são potências na base 10?
Toda potência de 10 é igual ao número formado
pelo algarismo
1, seguido de tantos zeros
quantas forem as unidades do expoente.
Acompanhe os exemplos a seguir.
1
10 = 1 0
10 2
10
3
10
= 1 00
-4
-5
10
= 1000
= 0,000 1
= 0,00000 1

6. E o que vem a ser notação científica?
Observe as informações na forma de potência.
No Sistema Internacional de Unidades (SI), a
unidade de carga elétrica é o coulomb (C). O valor
da carga do próton e do elétron é denominado
quantidade de carga elementar (e) e possui o
valor de:
e=1,6 .10-19 C

7. Órbita geoestacionária
Uma órbita é considerada geoestacionária quando esta
órbita é circular e se processa exatamente sobre o equador da
Terra, e a sua rotação acompanha exatamente a rotação da
Terra.
É o caso da maioria dos satélites artificiais de comunicações
e de televisão que ficam em órbitas geoestacionárias
Para que um satélite permaneça sempre sobre um determinado
ponto da superfície da Terra sem a necessidade de propulsão
vertical e horizontal, ele deve orbitar sempre a uma distancia
fixa de 35 786 km acima do nível do mar, no plano do equador
da Terra. Isso independente da massa (peso) do satélite.

8. Este tipo de registro é chamado de
No exemplo anterior esse comprimento (d) do raio do Sol, é de aproximadamente
696 milhões de metros ou:
d ≈ 696 000 000 m
Para evitar tantos zeros, podemos usar as potências de 10. Assim, d pode ser escrito de
outro modo:
d = 696 000 000 m = 6,96 x 108 m
Mas o que nos impediria de escrever d como 696 X106 ? Ou como 69,6 x 107?

9. Portanto, a notação científica surge como uma forma de padronizar essa simplificação, na
.
escrita, com potências de 10 e, ao mesmo tempo, dar a ideia imediata da grandeza do número
com o qual estamos lidando.
A notação científica também fornece uma ideia clara da ordem de grandeza (bilhões,
milhões, milésimos etc.) e a sua representação deve seguir o raciocínio abaixo:
a x 10n
onde
1 ≤ l a l < 10
nє Z
n é a ordem de grandeza

10. Na notação científica, esses números são escritos como produto de dois fatores em que um deles
é uma
potência de 10
com expoente inteiro (positivo ou negativo) e o outro, chamado de
coeficiente, um número entre 1 e 10.
Melhor dizendo: na notação científica, o número deverá ter apenas um algarismo não nulo na
parte inteira.
a) 1 x 10 – 6
b) 5 x 10 – 6
c) 6,96 x 108

11. a) 3 275 = 3,275 x 103
3 casas decimais
b) 0, 00056 = 5,6 x 10 – 4
4 casas decimais para a direita
c) 2 8 , 5 = 2,85 x 10 (neste caso não se escreve o algarismo 1 como expoente de 10.)
uma casa decimal

12. Então, vamos ver como fica a distância entre a Terra e o Sol com a notação científica?

13. E a carga do elétron, como fica?

15. Agora que você já sabe o que é notação científica e potência de 10, vamos ver um
exemplo prático na área de mecânica que envolve dilatação térmica.
Dilatação térmica é a mudança de tamanho que todos os materiais
apresentam quando são aquecidos.
Esta variação depende de uma constante característica de cada
material. Essa constante é conhecida como coeficiente de dilatação
térmica, e é representada pela letra grega α.
Lo
T1
T2
L
L
L = L0 
T

16. Em diversos problemas de física e mecânica usamos o coeficiente de dilatação linear, (que
chamamos de α) e que em geral tem muitas casas decimais. Nesses casos, os cálculos ficam
mais fáceis com o uso da notação científica. Acompanhe no exemplo a seguir:
Uma peça de vidro de 250 mm de comprimento em temperatura ambiente (25ºC) foi
aquecida a 500ºC. Qual foi o aumento do comprimento da peça após o aquecimento?
Considere:
 a variação de temperatura (t = 500 - 25),
 coeficiente de dilatação do vidro (α= 0,0000005)
L= Li α t

17. Solução:
Sabendo que
L= Li α t
L=?
α= 0,000 000 5
Li= 250
t= 475
L= 0,000 000 5 x 250 x 475
Observe como essa multiplicação
fica mais compacta e
simples com o uso da notação
científica.
L= 5 x 10-7 x 2,5 x 102 x 4,75 x 102
L= (5 x 2,5 x 4,75) x 10-7 + 2 + 2
L= 59,375 x 10-3
L= 5,94 x 10-2

18. Navegando...
Você pode obter mais informações sobre os assuntos que tratamos na internet. Algumas
sugestões de sites:
Textos: http://www.matematicamuitofacil.com/notacaocientifica.html
http://fisicacom.blogspot.com/2009/03/as-potencias-de-10-ordem-de-grandeza.html
Vídeo: http://www.youtube.com/watch?v=zml2ce_PN4Q
http://www.youtube.com/watch?v=7LIlBdhETc8

19. Agora é sua vez!
Teste os seus
conhecimentos.
1. Em 1972 a nave americana “Pionner 10” percorreu 5 900 000 000 km, estabelecendo um recorde
na corrida espacial. Dê a notação científica desta distância em km.

20. 2. Uma molécula é a menor parte de uma substância pura. O físico italiano Avogadro(1776- 1856)
mostrou que 18 g de água encerram cerca de 6,02 x 1023 moléculas. Calcule o valor aproximado do
número de moléculas contidas num miligrama de água.
3. A que temperatura foi aquecida uma peça de alumínio de 300 mm de comprimento e que sofreu
um aumento de comprimento (L) de 0,5 mm?
Dados: Fórmula da dilatação térmica L= Li α t, Temperatura ambiente = 26ºC, coeficiente de
dilatação do alumínio (α = 0,000 024)

21. Gabarito
Confira suas
respostas!
1. 5,9 x 109 km
2. 3,34 x 1019 moléculas
3. 69,4 C

22. Referências
Bibliográficas
1.
SILVEIRA, Ênio e MARQUES, Cláudio. Matemática vol. 4 . São Paulo: Moderna, 1995 .
2.
FRANÇA , Hélio. Mecânica – Mecânica Aplicada/ FAETEC- ETER. Rio de Janeiro, 2008.
3.
Fundação Roberto Marinho,TELECURSO 2000 - Calculo Técnico – Aula 2