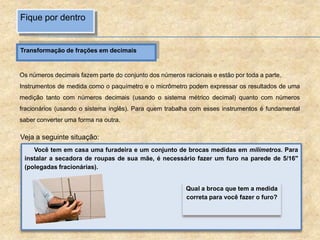
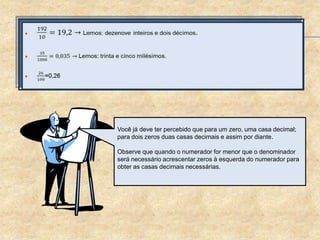
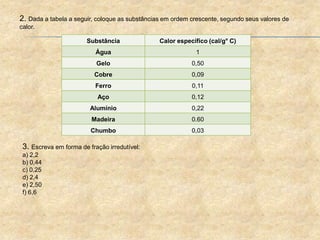
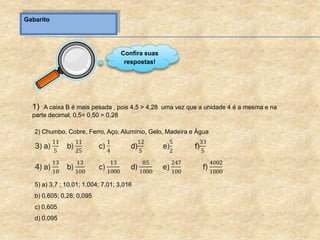
O documento aborda a importância dos números decimais na mecânica, incluindo como convertê-los de frações em decimais e vice-versa. Ele exemplifica situações práticas, como medir materiais e comparar valores, destacando a necessidade de conhecimento em operações com frações e medidas decimais. Além disso, oferece exercícios práticos para testar o entendimento sobre o conteúdo apresentado.

1. MATEMÁTICA PARA MECÂNICA

2. Vamos começar?
Ao folhear uma apostila de máquinas térmicas, você pode se deparar com uma tabela de custo
comparativo entre materiais. Veja o exemplo:
Material Custo relativo
aço carbono estrutural 1,00
aço carbono qualificado 1,15
ferro fundido 0,95
alumínio 2,50
titânio 41,00
Custo de materiais envolve o conhecimento de um sistema monetário e, para registrar
e operar com valores monetários, temos que utilizar números decimais.

3. Você consegue pensar em outras situações em que você utiliza números
decimais nas práticas da mecânica?
Viu como utilizamos os números
decimais, no nosso dia a dia,
muito mais do que imaginamos?

4. Fique por dentro
Transformação de frações em decimais
Os números decimais fazem parte do conjunto dos números racionais e estão por toda a parte.
Instrumentos de medida como o paquímetro e o micrômetro podem expressar os resultados de uma
medição tanto com números decimais (usando o sistema métrico decimal) quanto com números
fracionários (usando o sistema inglês). Para quem trabalha com esses instrumentos é fundamental
saber converter uma forma na outra.
Veja a seguinte situação:
Você tem em casa uma furadeira e um conjunto de brocas medidas em milímetros. Para
instalar a secadora de roupas de sua mãe, é necessário fazer um furo na parede de 5/16"
(polegadas fracionárias).
Qual a broca que tem a medida
correta para você fazer o furo?

5. Para resolver esse problema, você vai precisar converter as polegadas fracionárias em
frações decimais de milímetros e depois.... converter essas frações em decimais,
conforme feito a seguir:
= 7, 937 mm
Os números decimais podem ser obtidos através de qualquer racional na forma de
fração, basta efetuar a divisão do numerador pelo denominador.
Vamos ver como isso funciona?

6. Observe outros exemplos de números racionais na forma decimal:
As frações apresentadas no quadro anterior são frações decimais, ou seja, frações cujo
denominador é uma potência de 10. Esse tipo de número racional é o mais fácil de ser
transformado da forma fracionária para a forma decimal, pois requer apenas divisões por 10, 100,
1000, ...
Para escrever uma fração decimal na forma de número decimal, não precisamos efetuar a
divisão. Basta tomamos o numerador e nele colocamos uma vírgula, de modo que a quantidade de
algarismos da parte decimal, contada da direita para esquerda, seja igual à quantidade de zeros
que aparecem no denominador.
É o que comumente chamamos de “andar com a vírgula”.
Veja o exemplo a seguir:

7. Você já deve ter percebido que para um zero, uma casa decimal;
para dois zeros duas casas decimais e assim por diante.
Observe que quando o numerador for menor que o denominador
será necessário acrescentar zeros à esquerda do numerador para
obter as casas decimais necessárias.

8. Transformando números decimais para a forma fracionária
Por vezes é necessária a conversão no sentido inverso, como quando temos uma medida em
milímetros e precisamos transformar em polegadas fracionárias. Veja o exemplo a seguir:
No almoxarifado de uma empresa mecânica está uma chapa de alumínio de 1,588 mm de
espessura, mas é necessário descobrir sua medida em polegada fracionária.
Fique tranquilo: a conversão de um número da forma decimal para a forma fracionária
é ainda mais simples. Observe os exemplos a seguir:
O que fazer?

9. Podemos concluir que:
Para escrever um número decimal na forma de fração decimal, primeiro retiramos a vírgula do
número. Esse número, sem vírgula, será o numerador da fração. O denominador será uma
potência de 10 em que a quantidade de zeros será igual à quantidade de algarismos da parte
decimal do número dado.

10. Aprofunde seus conhecimentos sobre frações e decimais, assistindo
ao vídeo:
http://www.youtube.com/watch?v=dBWQmxsfQuQ

11. Comparação de números decimais
Comparar dois números decimais é determinar se eles são iguais ou se um deles é maior do que o
outro. Você consegue imaginar situações aonde essas comparações são úteis e necessárias?
Comparar valores monetários, medidas de comprimento, são
exemplos de situações importantes do nosso cotidiano e que exigem
a comparação de números decimais.

12. 1º Caso
Quando as partes inteiras são diferentes, o maior número é o que tem a maior parte inteira.
Exemplo;
• 6,7 > 5,9 ,pois 6 inteiros é maior do que 5 inteiros
• 15, 8 < 16, 8 , pois 15 inteiros é menor do que 16 inteiros
Quando as partes inteiras são iguais, o maior é o que tem a maior parte decimal.
Exemplo:
5, 3 < 5, 4 , pois 3 décimos é menor do que 4 décimos
5,37 < 5,4 (Neste caso teremos que igualar o número de casas decimais, acrescentando zeros)
Veja o raciocínio:
3,6 > 3,54 , pois 3,6 = 3,60 e 60 > 54
2º Caso
Ao fazermos a comparação
entre dois números decimais,
temos dois casos a considerar:

13. Teste seus conhecimentos passeando por essa atividade de localização de decimais na reta:
Professor Vaz Nunes 2008 / Ovar / Portugal © Nenhuns direitos reservados, excepto para fins comerciais.
Por favor, não coloque esta PPT em mais nenhum sítio da Internet.
C T A G R A D U A D AER
COMEÇA

14. Navegando...
Fique por dentro dos decimais.
Acesse:
http://www.slideshare.net/guestdc3a85/nmeros-racionais-expressos-na-forma-decimal-2519868
História dos Números Decimais da Turma da Mônica:
http://www.slideshare.net/kov0901/histria-dos-nmeros-decimais-6023932

15. Agora é a sua vez!
1. Uma placa de aço A foi colocada em uma balança, que marcou 4,28 kg. Uma segunda placa
B, foi colocada na mesma balança, que agora marcou 4,5 kg. Qual das duas placas é mais
pesada? Por quê?
Teste os seus
conhecimentos.

16. 2. Dada a tabela a seguir, coloque as substâncias em ordem crescente, segundo seus valores de
calor.
Substância Calor específico (cal/g° C)
Água 1
Gelo 0,50
Cobre 0,09
Ferro 0,11
Aço 0,12
Alumínio 0,22
Madeira 0.60
Chumbo 0,03
3. Escreva em forma de fração irredutível:
a) 2,2
b) 0,44
c) 0,25
d) 2,4
e) 2,50
f) 6,6

17. 4. Dê a fração correspondente a cada um dos números decimais a seguir:
a) 1,3
b) 0,13
c) 0,013
d) 0,085
e) 2,47
f) 4,002
5. Considere os números decimais a seguir:
1, 0 0 0 4
0 , 2 80 , 6 0 5
3 , 0 1 6
0 , 0 9 5
1 0 , 0 1
7 , 0 1
3 , 7

18. 5. Dentre eles, identifique:
a) Os maiores que 1.
b) Os menores que 1.
c) Os que estão entre 0,5 e 1.
d) Os menores que 0,1.

19. Gabarito
1) A caixa B é mais pesada , pois 4,5 > 4,28 uma vez que a unidade 4 é a mesma e na
parte decimal, 0,5= 0,50 > 0,28
2) Chumbo, Cobre, Ferro, Aço, Alumínio, Gelo, Madeira e Água
5) a) 3,7 ; 10,01; 1,004; 7,01; 3,016
b) 0,605; 0,28; 0,095
c) 0,605
d) 0,095
Confira suas
respostas!